Математическое моделирование тепломассообменных процессов в ванне руднотермических печей позволяет учитывать возникновение и влияние тепловых и гидродинамических неоднородностей на энергоэффективность функционирования печи [1].
Глубокое осмысление взаимозависимости и связи гидродинамики, тепломассообмена, химико-технологических и фазовых взаимодействий на параметры функционирования печей достигается полным анализом всех процессов происходящих в ванне печи [2].
Принципиально важно цельно представлять теплоэнергетическое состояние руднотермической печи для обнаружения и недопущения таких побочных проявлений, как: повышенный износ обмуровки в шлаковом пространстве и наличие устойчивого проявления гарнисажного горизонта; обеспечения наименьших термонапряжений в обмуровке корпуса и электродах; контролировании энергообмена в зоне шихты и спекания электродов [3].
Так как эти явления косвенно или прямо связаны друг с другом и значительно обеспечиваются режимными параметрами функционирования печей и их конструкциями, то проявляются очевидные направления акцентирования дальнейших теоретических разработок [4]. В этом смысле, облегчается проблема единства структуры математических моделей для описания энерго-технологических процессов, протекающих во всех зонах ванны руднотермической печи [5].
Построение математической модели процессов переноса в ванне руднотермической печи
Система уравнений для описания тепломассообменных процессов в руднотермической печи содержит уравнения сохранения: газовой компоненты, кокса, шлака и Р2О5. Уравнения динамики для каждой фазы и уравнений энергии для всех компонент [6].
Область реакции руднотермической печи образована многослойной массой частиц кокса, которые вместе с расплавом движутся вниз, с протекающими восстановительными реакциями окислов в жидкой фазе на поверхностях коксовых частиц.
Оксид углерода – это газовый компонент восстановительной реакции, перемещающийся в противотоке, барботирующий в расплаве, интенсифицирующий переносные процессы. Математическое описание теплообмена в данной системе представляет собой уравнения сохранения энергии и массы твёрдой, газовой и жидкой фаз в тензорной форме [7].
Уравнение сохранения массы:
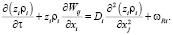
Уравнение динамики:
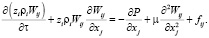
Уравнение сохранения тепловой энергии:
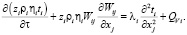
Уравнение распределения электрического потенциала
div(gradje) = 0,
где fг i = [mгrг – rшл (1 – mг )]g – cf (Wг i – Wшл i), сf – коэффициент сопротивления;
cf = 0,5c0 rшл mг SB |Wг i – W шл i |/Vв;
c0 = 24(1 + 0,15 Reв0.687) / Reв +
+ 0,42 Reв / (1 + 4,25*104Reв),
или
с0 = 8 / 3 (1 – mг)2.
Здесь Sв, Vв – поверхность и объем пузырьков газа, барботирующего через расплав; Reв = (Wг i – W шл i) dв /nг; dв – диаметр пузырьков газа;
fшл i = rшл g + cf ( Wг i – Wшл i) –
– cf s ( Sудк /ek3 ) rшл W2шл / 2,
где сfs – коэффициент трения, характеризующий взаимодействие шлака с частицами кокса;
сfs = 0.46 + 40 /Reшл + 2.28 / Reшл0.5;
Reшл = Wшл dэкв / nшл;
dэкв = 4 eк / Sудк,
где Sудк – удельная поверхность частиц кокса.
Источниковые члены для уравнений энергии фаз:
Qг V = aV (tшл – tг);
Qve = (1/re)grad2je – aV(tшл – tг) – Qхр wхр г,
где aV = Sудв aв – объемный коэффициент теплоотдачи; Sудв – удельная поверхность пузырьков газа.
Nu = aF dв /l = 2,0 + 0,6 Re0.6 Pr0.33,
где Re = Wг dв / nг – критерий Рейнольдса.
qф V = rм Qпл (dx / dt),
fi г = – Wг i mг сг f,
где
cг f = 150 mг (1 – e)2 / (d2м e2) +
+ 1,75 rг (1 – e)|Wг|/ dм.
Шихтовая зона руднотермической печи описывается уравнениями сохранения количества движения, энергии и массы в твердой и газовой фазе, пополненные уравнением переноса тепла для самоспекающегося электрода и имеют вид
Qг V = – aV (tг – tм);
Qм V = aV (tг – tм).
Замыкаемые соответствующими граничными и начальными условиями, приведенные уравнения обеспечивают проведение анализа и взаимосвязи основных параметров тепломассообмена на режим функционирования руднотермической печи.
Гидродинамический метод для анализа теплогидравлических режимов функционирования руднотермической печи
Представленная система уравнений очень сложна, а её решение сопряжено с определёнными трудностями, это особенно важно, если использовать модель в различных зонах руднотермической печи. Для такого случая сложность и размерность задачи увеличивается в три раза. Проблема становится неразрешимой с математической точки зрения [8].
Для случая применения эффективных коэффициентов переноса тепла в газовой и жидкой фазах уравнения энергии и динамики этих фаз связываются воедино, как некоторый континуум, который представляет теплоэнергетическую характеристику энергопереноса между фазами [9].
Соотношение в первом приближении фильтрационной динамики газа для потенциальной функции в многослойной массе частиц кокса, в расплаве с учетом источников выделения газа для плотности G имеет вид
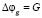 ;
;
уравнение сохранения массы реагирующей фазы имеет вид
(1 – εc)zwl∇Сlp2o5 – div(Dtgrad zClp2o5) + ωR = 0;
уравнение сохранения энергии имеет вид
λtΔt – (1 – εc)ρglcpglwl∇t = qv-QRωR;
уравнение распределения электрического потенциала принимает вид
ρelΔφel = 0.
Скорость газового потока выводится из закона газовой фильтрации через слой кокса:
wg = – k∇φg,
где ρgl – плотность газожидкостной смеси; k – эквивалентный коэффициент фильтрации; z – массовая доля компонента; λt – турбулентная теплопроводность расплава, определяемая барботажем газа; qv = ρe(∇φel)2 – удельная объемная электрическая мощность.
Для шихтовой области печи применяется система уравнений, включающая динамику газа в шихтовом слое, динамику перемещения дисперсных частиц шихты и уравнений передачи тепловой энергии в твердой и газовой фазе.
Соотношение для функции потенциала в первом приближении потока газа при фильтрации сквозь шихтовый слой: Δφg = 0; уравнение для потенциальной функции гравитационного движения дисперсных частиц: Δφm = 0, теплообмен в шихтовой области руднотермической печи определяется уравнениями
(1 – ε)cpm ρmwm∇tm – λmΔtm = αv(tg-tm),
εcрgρgwg∇tg – λgΔtg = αv(tm – tg),
где rт, rg, lт, lg, cрт, cрg, – плотность, теплопроводность и теплоемкость шихты и газов; av – коэффициент обмена тепловой энергией между шихтой и газом.
Скорость газового потока описывается исходя из предположения малости инерционных и вязкостных эффектов законом фильтрации Дарси:
wg = – kg∇φg.
Скорость схода шихты wm определяется как градиент соответствующего потенциала:
wm = – ∇φm,
получаемого в результате решения уравнения для потенциала.
Уравнение теплопереноса в самоспекающемся электроде
λеΔtе – ρеlcpеlwеl∇tе = qvе – QRеωRе ,
где ρеl, cрel, λе – плотность, теплоемкость и теплопроводность электродного материала; qvе, Qrе, ωRе – плотность джоулевого выделения тепла, неизотермический эффект пиролиза и его скорость; wеl – скорость перезапуска электродов.
Замыкаемые соответствующими начальными и граничными условиями, представленные уравнения обеспечивают анализ влияния главенствующих параметров тепломассообмена при функционировании в регламентном режиме ванны руднотермической печи.
В верхней части углеродистой области температура соответствует температуре шихтового плавления, а граничные условия в обмуровке ванны печи описываются условиями теплоэнергетического обмена сквозь обмуровку. Считается что стенки ванны печи теплоизолированны.
Сход шихты описывается граничными условиями на фазе плавления уравнением
ρm∂φm/∂n = –(λt∂tр/∂n – λm∂tm/∂n)/QL,
где ρm – плотность насыпной массы шихты, QL – теплота плавления шихты, ∂tр/∂n – градиент температуры в расплаве области плавления.
Для электрического потенциала граничные условия принимают вид: на электродах φеl = φele; в подовом пространстве φеl = 0; на шихтовой поверхности ∂φеl/∂n = 0; на границе раздела зон
φеl k = φеl k+1 и ρel k∂φеl k/∂n = ρel k+1∂φеl k+1/∂n,
где rel – удельная электрическая проводимость, k – расчётный номер пространства ванны руднотермической печи.
В верхней части температура шихты обеспечивается температурой внешней среды. Обмуровка печи полагается полностью теплоизолированной. Температура шихты, подаваемой в печь, соответствует температуре окружающей среды, и на фронте плавления – температуре плавления минеральной доли шихты [10].
Температура газа на выходе из области реакции представляется как средняя температура по расплаву в заданном сечении.
Фронт плавления в шихте, учитывая непроницаемость обмуровки стен ванны печи, описывается уравнениями граничных условий сохранения массы концентрации P2O5.
Математическое описание тепломассообменных процессов в ванне печи получается разбивкой полной системы уравнений на частные уравнения и подсистемы, с учётом «замороженности» некоторых процессов и их локализации в области под электродом при поочерёдном решении последовательных задач в различных зонах. Возможна оценка в первом приближении поля температур в области интенсивного химического реагирования с учётом ряда допущений постоянства концентраций реагента в реакционной области, стационарности процессов в расплаве, независимости процессов энерговыделения и тепломассопереноса. Такой подход является обоснованным при учёте различий характерного времени реагирования и тепломассопереноса.
В исследовании представлены оценки параметров состояния ванны печи, учитывающие допущения, не искажающие основных положений по физико-химическому смыслу задачи и несильно сказывающиеся на окончательных расчётных результатах.
Обсуждение результатов
Системный анализ полученных результатов дает основание устанавливать закономерности распределения температур печных газов в пространстве под сводом, при изменении управляющих параметров: дозирование кокса, гранулометрический состав шихты, напряжение на электродах, выявить влияние режимов функционирования печи на слой гарнисажной обмуровки.
Рассматривая зону реакции как цилиндрическое пространство с осью симметрии, соответствующей оси электрода, упрощается математическое описание физико-химических процессов в расплаве на базе взаимовлияния трёх отдельных локализованных реакционных объёмов [11].
Выделение тепловой энергии в расплаве – это главный источник энергии, который определяет интенсивность протекания химических реакций в соответствующей области ванны печи. В соответствии с современными представлениями доля энергии в пространстве под сводом печи образуется на дуге, выделяющейся в области под электродом, какая-то часть при движении тока через область углерода в расплаве. Основная часть выделения тепла – это джоулевая тепловая энергия. Следовательно, очень важно определить факторы, оказывающие влияние на выделение тепла [12]. Плотность тока следует считать зависимой лишь от пространственных координат, а не от временных, так как электромагнитные процессы протекают намного быстрее процессов переноса теплоты.
Объёмное распределение мощности обеспечивается стабилизацией реакционной области и выражается характерным смещением части объёмной мощности в сторону электрода. Увеличивается также радиус реакционного тигля – rр.
Наращивание гарнисажного слоя на стенки ванны в расплаве позволяет уменьшить радиус реакционного тигля и обеспечивается распределением потенциала, способствующим значительному интенсивному выделению тепла на границе тигля. Оно препятствует дальнейшему сокращению реакционной зоны (рисунок).
Обнаружена экспоненциальная зависимость выделения тепловой энергии по глубине зоны реакции. Выделение теплоты локализовано в окрестности электрода. Этот факт дает основание предполагать, что электрическое поле электродов в расплаве трехэлектродных руднотермических печей мало взаимосвязаны между собой. Суммарное выделение тепловой энергии в трехэлектродной печи производится, с использованием свойства аддитивности.
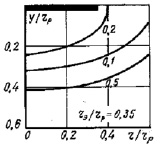
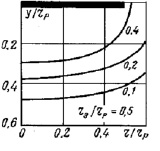
Распределение выделения тепловой энергии в реакционной зоне печи
Степень интенсивности выделения теплоты сильно уменьшается по глубине ванны. Явно наблюдается локализация источников теплоты в зонах около электрода, а неоднородность в условиях различного заглубления электродов.
Заключение
Итак, основная доля тепловой энергии реакционных тиглей выделяется в области под электродом, и тепловыделяющий горизонт слоя почти не выходит за рамки коксовой зоны. Шлак имеет другое от коксовой области удельное электрическое сопротивление. Выявлено, что такие неоднородности мало оказывают влияние на распределение теплоэнергетических источников.
Работа выполнена при финансовой поддержке РФФИ, грант № 18-29-24094 MK.
Библиографическая ссылка
Бобков В.И. МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ПРОЦЕССОВ ПЕРЕНОСА В ВАННЕ РУДНОТЕРМИЧЕСКОЙ ПЕЧИ НА ОСНОВЕ ГИДРОДИНАМИЧЕСКОГО ПОДХОДА ДЛЯ АНАЛИЗА ТЕПЛОГИДРАВЛИЧЕСКИХ РЕЖИМОВ ФУНКЦИОНИРОВАНИЯ // Современные наукоемкие технологии. 2019. № 9. С. 43-47;URL: https://top-technologies.ru/ru/article/view?id=37663 (дата обращения: 05.03.2026).



