Один из первых двусторонних протоколов открытого распределения ключей предложен в 1976 г. У. Диффи, М. Хеллманом. Протокол основан на трудности решения задачи дискретного логарифма в мультипликативной группе большого порядка с образующей α.
1. A→B: αx mod p
2. B→A: αy mod p (DH)
3. A: kAB = ((ay)x) mod p
4. A: kBA = ((ax)y) mod p
Несмотря на то, что задача дискретного логарифма NP-трудна, существует вариант атаки «человек посередине» активного противника (MITM), против которого DH-протокол бессилен, ввиду отсутствия в нем аутентификации сторон. Для проведения атаки противник С не обязан решать задачу дискретного логарифмирования, однако, пользуясь отсутствием аутентификации в (DH), встает посередине между A и В, представляясь для А абонентом В, для В соответственно абонентом А. Далее, не обнаруживая себя, он осуществляет подмену передаваемых значений на свои значения, не решая при этом задачу дискретного логарифма и контролируя после завершения протокола обе части разорванного канала связи между А и В.
1. A→C: αx mod p
2. C→B: αx mod p
3. B→C: αy mod p
4. C→A: 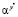 mod p (MITM DH)
mod p (MITM DH)
5. A: kAC = 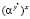 mod p
mod p
6. B: kBC = 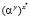 mod p
mod p
7. C: kAC = 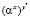 mod p
mod p
8. C: kCB = 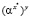 mod p
mod p
В связи с востребованностью DH-протокола в приложениях, приведены многочисленные варианты усиления DH в направлении аутентификации сторон А и В, с относительным сохранением свойств протоколов открытого распределения колючей. Далее мы воспользуемся только описанием направлений усиления, пользуясь детальным обзором в книге [1].
Первые усиления основаны на использовании доверенного центра и введении доверенных сертификатов, связывающих участников протокола X∈{A, B} со значениями ax, ay и подписью доверенного центра SigT:
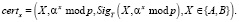
В первоначальном варианте семействе протоколов MTI [1, с. 174] без участия доверенного центра предполагается у участников протокола секретных ключей, и формулы выработки секретного ключа мультипликативно зависят от их значений. В результате MITM-атаки противника, все стороны протокола получат различные ключи, что будет обнаружено в результате чтения переданных сообщений. В последующих усилениях MTI появляется зависимость и от открытых ключей участников работы протокола.
В нашей работе в рамках модели секретной связи К. Шеннона мы предлагаем аддитивные протоколы порождения симметричного ключа и обмена данными, противодействующие атаке человек посередине. Для этого нами используется предварительно созданная Отправителем А и Получателем В и разнесенная на соответствующие устройства общая память – целочисленное множество значений D = {d1…dn}. Строго говоря, использование общей памяти выходит за рамки протоколов открытого распределения ключей, и само использование общей памяти достаточно сильно идентифицирует канал связи между абонентами А и В. Однако с учетом того, что значения общей памяти, вообще говоря, произвольны и не являются дополнительными идентификаторами, а представленные протоколы не требуют привлечения третьей доверенной стороны – арбитра, а также секретных и публичных ключей абонентов секретной связи, мы считаем, что такой подход имеет право на существование.
Цель: разработка протоколов создания симметричного ключа и обмена сообщениями между Отправителем и Получателем на основе общей памяти, устойчивых по отношению к активному и пассивному противнику в канале связи.
Определения
Обозначим здесь и далее m > 1 размер симметричного криптографического ключа k, 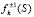 функции симметричного шифрования/расшифрования и пусть Hk(S) – ключевая хэш-функция, сильно сопротивляющаяся поиску коллизий.
функции симметричного шифрования/расшифрования и пусть Hk(S) – ключевая хэш-функция, сильно сопротивляющаяся поиску коллизий.
Определение 1: Назовем общей памятью Отправителя (A) и Получателя (В) – согласованное между Отправителем и Получателем и разнесенное на устройства Отправителя и Получателя числовое множество D = {d1…dn}, n > 1, n < m.
В качестве элементов D могут выступать файлы, расположенные на информационных носителях Отправителя А и Получателя В, и только на них. Смысл значений D = {d1…dn}, n > 1, n < m нас не интересует. После разнесения общей памяти на устройства пользователей множество D = {d1…dn}, n > 1, n < m и его элементы, если это необходимо, снабжаем индексом X∈{A, B} для того, чтобы подчеркнуть, на каком устройстве мы рассматриваем само множество и его элементы. Наличие общих элементов Отправителя А и Получателя В, конечно, выходит за рамки модели секретной связи К. Шеннона, однако не противоречит модели угроз Долев – Яо, предложенной в 1981 г. Д. Долевым и А. Яо для детального описания среды, в которой происходит обмен шифрованными сообщениями, при наличии в ней пассивного или активного противника С.
Процедура создания общей памяти, выработки первого значения симметричного ключа и первого ключевого хэша не предполагает использования канала связи и выполняется в момент создания множества D.
Определение 2. Свяжем со значениями общей памяти предварительный ключ
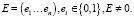 (1)
(1)
Для выработки симметричного ключа используем аддитивную формулу
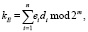 (2)
(2)
где, напомним, m – размер сеансового ключа шифрования.
Утверждение 1: Пусть D = {d1…dn}, n > 1, n < m – общая память, созданная на устройствах отправителя и получателя (DA = DB) в модели секретной связи К. Шеннона, E – предварительный ключ, kE – сеансовый ключ. Тогда противник С по значению предварительного ключа E ≠ 0 не может построить симметричный ключ kE. Это можно выразить в терминах условной энтропии К. Шеннона. H(S|Si): меры неопределенности значения S при условии обладания значением Si
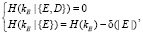 (3)
(3)
где 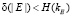 .
.
В терминах условной энтропии Шеннона, понимаемой относительно вероятностных распределений для значений kE, E, D, первое равенство означает, что неопределенность значения ключа kE по значениям теней E, D полностью снимается. Второе соотношение определяет меру неопределенности симметричного ключа для противника С при перехвате предварительного ключа и несовершенность схемы разделения секрета следует из работы [2].
Доказательство использует технику (2,2) пороговых схем разделения секрета [2], для которых секретным значением является ключ kE. Долями секрета являются соответственно значения D, E.
В силу разбалансирования размеров долей секрета друг относительно друга, схема разделения, порождаемая формулой (2), является (2,2) пороговой, не идеальной, не совершенной. Математическая конструкция подобных схем исследована в работах Kurosawa. В частности, из неидеальности СРС вытекает последняя формула в (3).
Криптографические протоколы создания симметричного ключа и передачи данных
Пусть противник C в канале связи пассивный, перехватывает весь трафик в канале связи, но не имеет возможности подмены.
Приведем протокол создания симметричного ключа, безопасный по отношению к пассивному противнику.
1. 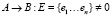
2. 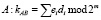 (4)
(4)
3. 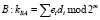
В силу утверждения 1 противник С не имеет возможности построить значение kBA = kAB.
Для противодействия активному противнику, который может перехватывать и видоизменять передаваемый трафик, воспользуемся ключевой хэш-функцией 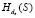 с ключом de – предыдущим сгенерированным сеансовым ключом. Приведем двусторонний протокол формирования нового симметричного ключа, безопасный по отношению к активному противнику
с ключом de – предыдущим сгенерированным сеансовым ключом. Приведем двусторонний протокол формирования нового симметричного ключа, безопасный по отношению к активному противнику
1. 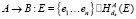
2. 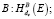 если
если 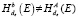 , то стоп
, то стоп
3. 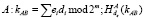
4. 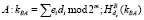 (5)
(5)
5. 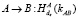
6. B: если 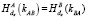 , то
, то 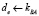 , иначе стоп
, иначе стоп
7. 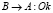
8. А: если Ok, то 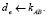
Нетрудно видеть, что такое усиление протокола (4), в силу свойств 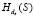 и утверждения 1, эффективно противостоит активному противнику в канале связи. В самом деле, противник на шаге (5.1) может легко изменить вектор Е, однако не может построить функцию
и утверждения 1, эффективно противостоит активному противнику в канале связи. В самом деле, противник на шаге (5.1) может легко изменить вектор Е, однако не может построить функцию 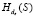 , так как не имеет доступа к общей памяти в модели Долев – Яо, хотя и знаком с ее описанием. В то же время абонент B, зная
, так как не имеет доступа к общей памяти в модели Долев – Яо, хотя и знаком с ее описанием. В то же время абонент B, зная 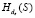 , легко может обнаружить факт подмены предварительного ключа E, на шаге (5.2) протокола передачи. Противник также может совершить перехват и подмену
, легко может обнаружить факт подмены предварительного ключа E, на шаге (5.2) протокола передачи. Противник также может совершить перехват и подмену 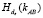 на шаге (5.5), разрушая протокол создания симметричного ключа, однако на шаге (5.6) этот факт также будет обнаружен без выработки значения OK.
на шаге (5.5), разрушая протокол создания симметричного ключа, однако на шаге (5.6) этот факт также будет обнаружен без выработки значения OK.
При обмене сообщениями отправитель посылает получателю сообщение, зашифрованное на выработанном ключе, при этом совместно с зашифрованным сообщением отправляет хэш-функцию на выработанном ключе,
1. 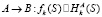
2. 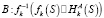 (6)
(6)
3. B: если 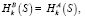 то Ok.
то Ok.
При корректном завершении работы протокола и равенстве значений хеш-функций на шаге (6.3), сообщение S считаем успешно переданным.
Дерево Дамгарда – Меркла и контроль целостности общей памяти
Существует принципиальная возможность удаленного контроля целостности общей памяти отправителя и получателя, использующая технику деревьев Дамгарда – Меркла. Дерево Дамгарда – Меркла – бинарное дерево, листовыми вершинами которого являются хэш-значения от элементов общей памяти, а внутренние вершины являются результатом попарной конкатенации пар смежных хэшей на соседнем нижнем этаже бинарного дерева (рис. 1). Структура деревьев Дамгарда – Меркла предложена в работе «A Digital Signature Based on a Conventional Encryption Function» Ральфом Мерклом, и сегодня находит свое применение в контроле целостности больших массивов цифровых данных, в частности в электронных валютах стандарта Bitcoin [3].
Преимущество структур Деревьев Дамгарда – Меркла следующие:
1. Деревья Дамгарда – Меркла позволяют обеспечивать целостность и достоверность данных.
2. Деревья Дамгарда – Меркла требуют небольшого объема памяти или дискового пространства, поскольку доказательства Дамгарда – Меркла являются логарифмическими по вычислительной сложности, а поэтому легкими и быстрыми.
3. Доказательства Дамгарда – Меркла требуют малого количества информации, которая должна передаваться по сетям связи.
4. Может использоваться любая из доверенных функций хэширования, которая сильно сопротивляется коллизиям.
Обозначим дерево Дамгарда – Меркла RDMX(D), X = {A, B}, построенное над общей памятью соответственно Отправителя для X = A и Получателя для X = B. Представленные выше старты протоколов порождения ключа и передачи данных можно завязать на успешное сравнение мастер-хешей RootHash(RDMA(D)) = RootHash(RDMB(D)) в противном случае, проигрывается парный протокол доказательства Меркла, позволяющий выловить различия в общей памяти Отправителя и Получателя.
Процедура порождения симметричного ключа на основе предварительного – критически важна для работы всех предложенных протоколов, несмотря на ее безопасность в смысле утверждения 1. Активный противник имеет возможность постоянно вмешиваться в протокол, на стадиях передачи данных в режиме подмены сообщений, разрушая работу протокола и обнаруживая себя. Существует конструкция, позволяющая избежать частого применения этого протокола создания симметричного ключа, основанная на выделении динамической компоненты в области общей памяти. Этот подход кратко обсудим в следующем разделе.
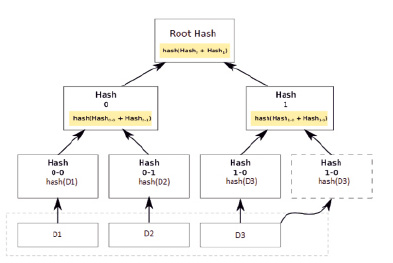
Рис. 1. Дерево Дамгарда – Меркла
Где D1…Dn – элементы общей памяти
Hash 0-0, 0-1 … N-N – листовые вершины дерева Дамгарда – Меркла
Hash 0, 1, N – вершины дерева Дамгарда – Меркла
RootHash – корневой хэш всего дерева Дамгарда – Меркла – мастер-хэ
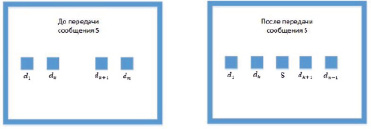
Рис. 2. Общая память с динамической компонентой
Динамическая общая память
Выделим в общей памяти статическую и динамические области D = {d1…dk, dk+1…dn}, {d1…dk} – статическая компонента общей памяти, и {dk+1…dn} – динамическая компонента общей памяти, представленная в виде очереди. Пусть S удачно переданное сообщение. Под удачно переданным сообщением подразумевается, что при передаче в протоколе (5) имеет место равенство значений на шаге (6.3), корректно завершающее работу протокола передачи. Перемещаем значение S в общую память на место значения dk+1 и перемещаем на одну позицию все значения общей памяти динамического сегмента {dk+1…dn}. Более точно изменение значения общей памяти выглядит следующим образом (рис. 2):
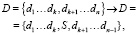
где di – элемент общей памяти,
S – передаваемое сообщение.
Такое динамическое перестроение общей памяти завершается автоматическим пересчетом значений общей памяти, пересчетом элементов деревьев Меркла RDMX(D), X = {A, B} и соответствующим изменением значения сеансового ключа (2) без передачи по протоколам (4–5) и изменения предварительного ключа.
Из такой конструкции перестроения общей памяти следует, что с использованием динамической компоненты общей памяти, можно не создавать новый симметричный ключ по протоколу (4–5), а просто пересчитать значения kAB = kBA в (2) по измененным значениям общей памяти, в том случае если элементы динамической области отмечены в предварительном ключе единицей.
Заключение
Выделенный подход использования общей памяти, конечно, выходит за границы протоколов открытого распределения ключей, так как заранее отправитель и получатель в канале связи договариваются об общей числовой базе. Однако отметим то, что значения общей памяти не обязаны служить идентификаторами пользователей, или их секретными и открытыми ключами, и имеют общий порядок. Кроме того, приведенные протоколы на завязаны на стандарты шифрования и хэширования. В частности, с использованием уникальности хэш-функции для Отправителя и Получателя 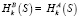 с неизвестным значением ключа для противника С, созданной на стадии протоколов (4–5) легко преобразовать сам протокол Диффи – Хеллмана, сделав его устойчивым к MITM атаке противника С.
с неизвестным значением ключа для противника С, созданной на стадии протоколов (4–5) легко преобразовать сам протокол Диффи – Хеллмана, сделав его устойчивым к MITM атаке противника С.
4. 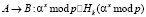
5. 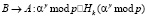
6. 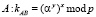 (DH*)
(DH*)
7. 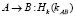
8. 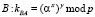
9. B: если 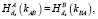 то Ok, иначе СТОП.
то Ok, иначе СТОП.
Для этого к передаваемым значениям в DH-протоколе на шаге (DH*.1-2) прикрепляем значение хэш-функции от передаваемых данных, где хэш-функция построена на ключе, сформированном по протоколу (5). Кроме того, на шаге (DH*.4) передается значение хэш от построенного ключа на стороне А. На шаге (DH*.6) сторона В либо подтверждает создание нового симметричного ключа в случае равенства значений хэшей, либо обнаруживает MITM-атаку противника С.
По терминологии документов международной организации Internet Engineering Task Force (IETF), существует современная классификация свойств, характеризующих безопасность криптографических протоколов, в которой выделены 20 пунктов, разделенные по 10 группам [1, с. 13–21].
Свойства безопасности, характеризующие основные протоколы
|
Протокол |
Свойство Gi |
||||||||||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
|
|
TLS |
× |
× |
× |
× |
× |
× |
× |
||||||||
|
TLS-v1.1 |
× |
× |
× |
× |
× |
× |
× |
||||||||
|
TLS-SPR |
× |
× |
× |
× |
× |
× |
× |
||||||||
|
TLS-sharedkeys |
× |
× |
× |
× |
× |
× |
× |
||||||||
Атака типа «человек посередине» нарушает свойства протокола безопасности G1, G2, G4, G5, G7, G13. Далее приведена таблица, в которой отмечено, какими свойствами безопасности обладает ряд криптографических протоколов семейства TLS (таблица).
Протокол Диффи – Хеллмана встроен в семейство TLS-протоколов [4], поэтому в таблице обращаем внимание на тотальную уязвимость протоколов семейства: TLS, TLS-v1.1, TLS-SRP, TLS-sharedkeys по отношению к свойствам G1, G2, G7, G13 в силу уязвимости DH к атаке активного противника «человек посередине». Представленные протоколы (5), (DH*) закрывают перечисленные уязвимости.
В заключение отметим, что протоколы (4), (5), (DH*), предложенные в работе, удовлетворяют требованиям безопасных аутентифицированных протоколов обмена ключами.
Понятие безопасного аутентифицированного протокола обмена ключами было введено У. Даффи, П. ван Ооршоном и М. Вайнером в 1992 г. в работе «Authentication and Authenticated Key Exchanges». По определению, такой аутентифицированный протокол безопасен, если при каждом выполнении протокола двумя участниками гарантируется выполнение двух условий:
1) если сторона А принимает идентификатор стороны В, записи в сообщениях, передаваемых обеими сторонами, осуществляются правильно;
2) никто кроме сторон А и В не может определить передаваемый ключ.
Протоколы (4), (5), (DH*), предложенные в работе, удовлетворяют этим свойствам, поскольку общая память для сторон А и В едина, то в вышеописанных свойствах 1–2 А и В можно поменять местами. Использование общей памяти в криптографических протоколах встречается не впервые и, в частности, использовано в работе [5].
С учетом использования общей памяти в канале секретной связи, протоколы (3), (4), (5), (DH*) ограничены в использовании, имеют парный, долговременный и безопасный характер секретной передачи данных для абонентов А, В, по отношению к противнику С в канале связи, как пассивном, так и активном.
Благодаря использованию динамической общей памяти удается снять одну из традиционных проблем симметричной криптографии – процедуру создания и передачи симметричного ключа. С динамическим изменением и синхронизацией общей памяти D с привлечением конструкции дерева Дамгарда – Меркла симметричный ключ kE по формуле (2) автоматически изменяется на устройствах А и В.
Работа выполнена при поддержке и финансировании Российского фонда фундаментальных исследований, грант № 18-01-00596А.
Библиографическая ссылка
Александров А.В., Сорокин И.И. ПРОТОКОЛЫ ВСТРАИВАНИЯ ОБЩЕЙ ПАМЯТИ В СИММЕТРИЧНЫЙ КАНАЛ СЕКРЕТНОЙ СВЯЗИ ДЛЯ ПРОТИВОДЕЙСТВИЯ MITM-АТАКАМ // Современные наукоемкие технологии. 2019. № 9. С. 14-19;URL: https://top-technologies.ru/ru/article/view?id=37658 (дата обращения: 06.02.2026).



