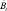В соответствии с одним из базовых положений дидактической инженерии [1, 2], освоение любой специальности через обучение представляет собой многостадийный развернутый во времени процесс развития формализаторских, конструктивных и исполнительских способностей обучаемого. Необходимый начальный уровень способностей определяется минимальным набором сведений и навыков, без наличия которых продуктивное обучение невозможно, а конечный уровень гарантирует обладание знаниями и компетенциями достаточными для успешной работы специалиста. Целью обучения является достижение требуемого конечного уровня способностей в течение заданного срока, который регламентируется нормативными документами. Все три типа способностей, подлежащих развитию, образуют единый комплекс в рамках каждой конкретной личности, и это должно обязательно учитываться при формировании стратегии достижения конечной цели. В настоящее время не существует строгих моделей, основанных на фундаментальных законах педагогики и психологии, описывающих поведение этого комплекса, поэтому вынесение обоснованных суждений о нем возможно только на основании обработки и анализа результатов статистических наблюдений. Заметим также, что единственным инструментом влияния на темп развития способностей является поток учебных проблем, сложность которых сопоставима с зоной ближайшего развития обучаемых.
Таким образом, процедура рациональной организации и планирования учебного процесса должна предусматривать решение следующих задач: разработку математической модели динамических изменений способностей в ходе обучения с учетом их взаимосвязи и взаимовлияния; построение усредненной траектории развития способностей для ансамбля обучающихся по результатам статистических наблюдений; разработку модели индивидуального развития способностей и алгоритм ситуационного управления процессом обучения.
Цель исследования: разработать математическую модель и алгоритм прогноза и оперативного управления учебным процессом.
Математическая модель изменения способностей в процессе обучения, параметры которой могут быть получены по результатам статистических наблюдений, предложена в работе [3]. Она представляет собой систему совместных одновременных регрессионных уравнений и имеет вид
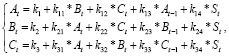(1)
где At – уровень развития формализаторских способностей на момент времени t; Bt – уровень развития конструктивных способностей на момент времени t; Ct – уровень развития исполнительских способностей на момент времени t; St – уровень сложности учебных проблем, предлагаемых обучающимся в момент времени t. Метки времени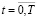 
соответствуют контрольным точкам (экзаменам, зачетам, коллоквиумам и т.п.), предусмотренным учебным планом, когда уровень способностей можно объективно оценить с помощью контрольно-измерительных материалов.
Система (1) относится к классу идентифицируемых моделей, и оценки параметров kij получаются посредством косвенного метода наименьших квадратов, который широко используется в эконометрических исследованиях [4, 5]. Реализация этого метода требует хотя и несложных, но довольно громоздких алгебраических преобразований. Для данной модели они подробно изложены и прокомментированы в статье [3]. Здесь рассмотрен пример применения данной модели к массиву, полученному по результатам длительных наблюдений за ходом обучения студентов по специальности «Информационные системы и технологии».
В таблице представлены данные о динамике изменения формализаторских, конструктивных и исполнительских способностей студентов.
Изменения усредненных способностей группы обучающихся, зафиксированные в девяти контрольных точках
|
t |
Статистические |
Сложность (системная) |
Вычисленные |
||||
|
At |
Bt |
Ct |
St |
Át |
|
?t |
|
|
0 |
0,5 |
1 |
0,2 |
0,6 |
0,5 |
1 |
0,2 |
|
1 |
1 |
2,2 |
0,6 |
1,3 |
1,3 |
2,07 |
0,52 |
|
2 |
2 |
3 |
1 |
2 |
1,93 |
2,91 |
1,02 |
|
3 |
2,5 |
4 |
1,5 |
2,7 |
2,5 |
3,91 |
1,51 |
|
4 |
3 |
5 |
2 |
3 |
3,02 |
5,04 |
1,99 |
|
5 |
4 |
6 |
3,5 |
4 |
3,99 |
5,95 |
2,98 |
|
6 |
5 |
7 |
4 |
5,3 |
5,02 |
7,04 |
4 |
|
7 |
6 |
8,5 |
5,5 |
6,5 |
6 |
8,47 |
4,97 |
|
8 |
7 |
10 |
6 |
7,7 |
6,99 |
10,13 |
5,94 |
|
9 |
8 |
12 |
7 |
9 |
8 |
12 |
7 |
Заметим, что каждый из элементов столбцов At, Bt, Ct вычислялся как среднее арифметическое соответствующих способностей по материалам нескольких академических групп. Это устраняет любые сомнения в статистической устойчивости и достоверности результатов. Обрабатывая наблюдения с помощью процедуры косвенного метода наименьших квадратов, этапы которой подробно изложены в [4, 6], находим численные значения параметров системы (1):
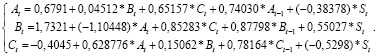(2)
Результаты расчетов, реализованных в рамках этой модели, также содержатся в таблице (см. столбцы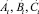 
). Их проверка посредством традиционных статистических методик подтвердила адекватность полученной модели, однако даже простое сравнение столбцов At, Bt, Ct со столбцами 
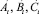убеждает в удовлетворительном качестве моделирования. На диаграмме рис. 1 наглядно представлен процесс динамического изменения At, Bt и Ct способностей в процессе обучения
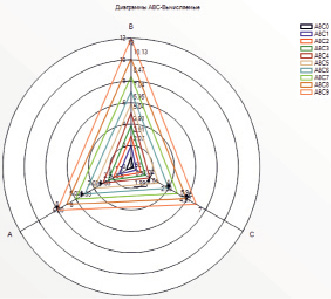
Рис. 1. Процесс динамического изменения At , Bt , Ct способностей в ходе обучения
Поскольку все значения At, Bt, Ct способностей, как наблюдаемые, так и вычисленные в ходе моделирования, жестко связаны с определенными метками времени, последовательности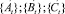 
представляют собой траектории развития способностей через обучение. На рис. 2 эти траектории изображены графически
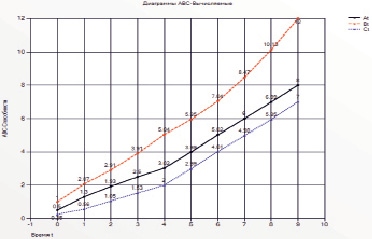
Рис. 2. График траекторий развития At , Bt , Ct способностей через обучение
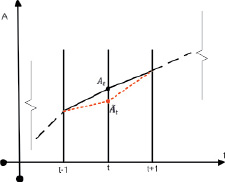
Рис. 3. График выработки оперативного корректирующего воздействия на обучаемого в режиме реального времени
Заметим, что они дают картину усредненной оценки изменения способностей для некоторого среднестатистического обучаемого в наблюдаемой группе по данной специальности. Модели такого типа являются сугубо индивидуальными, как большинство регрессионных моделей, и ориентированными на описание только того процесса, по которому собран массив статистических наблюдений. Действительно: характер взаимовлияния формализаторских, конструктивных и исполнительских способностей у обучающихся информатике будет существенно иным, нежели у студентов медиков или филологов. Естественно, что это проявится в виде значительных различий коэффициентов системы (2).
Полученные результаты могут быть с успехом использованы для решения задач стратегического управления и планирования: разработки учебных планов и программ; прогнозирования уровня развития способностей, который может быть достигнут в ходе обучения; оценки степени сложности учебных проблем, достаточной для обеспечения высокой эффективности обучения. Однако для организации оперативного (ситуационного) управления учебным процессом на отдельных участках траектории нужны иные подходы, позволяющие в режиме реального времени сформулировать и реализовать соответствующие управляющие воздействия. Рассмотрим ситуацию, когда оперативное управляющее вмешательство становится необходимым, и построим ее модель.
Возьмем участок траектории развития какой-либо способности, например А, на отрезке [t – 1, t + 1] и положим, что обучаемый не достиг в точке t заданного уровня способности At, остановившись на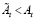 
, что зафиксировано с помощью имеющихся контрольно-измерительных средств. Для успешного продолжения процесса обучения необходимо рассчитать управляющее воздействие, интенсивность которого была бы достаточной для возвращения обучаемого к моменту времени t + 1 на требуемую траекторию развития (рис. 3).
Как было отмечено выше, изменение способностей в ходе обучения не может происходить скачкообразно. Уровень способностей в момент времени t + 1 зависит от состояния их в предшествующий момент и потока усвоенных учебных проблем, предложенных на интервале [t, t + 1]. Таким образом, развитие способностей через обучение обладает признаками Марковских процессов, и это обстоятельство должно быть обязательно учтено при построении математической модели и алгоритма оперативного управления.
Принимая во внимание высказанные соображения, изменение способностей на отрезке [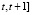
можно описать соотношениями
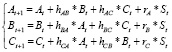, (3)
где hAB, hAC, hBA, hBC, hCA, hCB – коэффициенты взаимного влияния способностей друг на друга, а rA, rB, rC – оценки интенсивностей потока учебных проблем сложности St. Уравнения (3) не образуют систему, и для отыскания их параметров метод наименьших квадратов использовать нельзя, поскольку значения At, Bt, Ct получены по результатам не статистических, а разовых наблюдений в режиме реального времени.
Решение вопроса идентификации параметров этих уравнений вытекает из того фактора, что все они являются оценками тесноты связи между различными способностями, в качестве меры которой принято использовать величины коэффициентов парной линейной корреляции rAB, rAC, rBC. Они могут быть легко найдены по данным статистических наблюдений, выполненных в контрольных точках, и вполне пригодны для оценки взаимовлияния способностей, поскольку в рамках определенной специальности (предметной области) практически не меняются от выборки к выборке, т.е. обладают свойством устойчивости.
Однако отождествлять коэффициенты парной корреляции с соответствующими параметрами модели (3) нельзя, поскольку величины rAB, rAC, rBC не позволяют оценить эффект «чистого» влияния пары способностей друг на друга, ввиду присутствия третьей, которая неразрывно с ними связана. Это актуализирует проблему элиминирования постороннего влияния, которая решается путем вычисления частных коэффициентов корреляции. При наличии одной результативной и n факторных переменных они могут быть найдены с помощью известного рекуррентного соотношения [4, 5]
(4)
где точка в индексах отделяет факторы, влияние которых элиминируется.
Для нашего случая
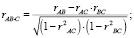
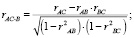
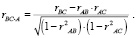(5)
Таким образом
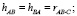
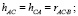
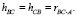(6)
Точки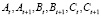 
принадлежат основной траектории и их положение известно. Координаты точек 
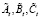определяются непосредственно в момент времени t по результатам контроля и характеризуют фактическое состояние способностей обучаемого на этот момент. И, если они расположены вне траектории развития, уравнения (3) дают возможность найти, насколько необходимо изменить интенсивности потока учебных проблем rA, rB, rC, чтобы к моменту t + 1 вернуться на расчетную траекторию.
Проиллюстрируем технику реализации предложенного алгоритма на числовом примере. Пусть в контрольной точке при t = 4 установлено, что кто-то из обучаемых по двум из трех показателей не достиг уровня усредненных траекторий, представленных на рис. 2, и показал результаты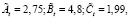 
вместо требуемых At = 3,02; Bt = 5,04, Ct = 1,99. Выясним, как надлежит изменить величину интенсивности потока учебных проблем, сложность которых на этом этапе равна St = 3 (таблица), чтобы к следующей контрольной точке при t = 5 обучаемый ликвидировал отставание и вернулся на рекомендованную траекторию развития.
По материалам того же массива наблюдений, что был использован для отыскания коэффициентов системы (2), были вычислены коэффициенты парной линейной корреляции rAB = 0,15; rAC = 0,22; rBC = 0,29. Как и следовало ожидать, их значения невелики, поскольку в любой представительной группе присутствуют люди различного развития и одаренности. Далее по формулам (5) были найдены частные коэффициенты корреляции rAB?С = 0,092; rAС?B = 0,1865; rBC?A = 0,266. Таким образом, согласно (6),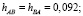 
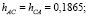
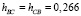. Подставляя найденные значения и данные таблицы, соответствующие четвертой и пятой меткам времени в выражения (3), получим
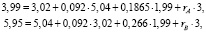
откуда rA = 0,037; rB = 0,047. Это величины интенсивности потока учебных проблем, соответствующих этапу между четвертой и пятой контрольными точками, при которых обучаемый не покидает расчетные траектории развития. Поскольку комплекс учебных проблем невозможно строго разделить по различным типам способностей, гарантированное достижение результата дает большее из найденных значений rB = 0,047. Реализуем теперь тот же алгоритм для точек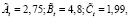 
две из которых не принадлежат расчетным траекториям
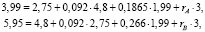
откуда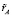 
= 0,137; 
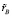= 0,123. По упомянутым выше соображениям выбираем в качестве ориентира большее из найденных значений 
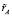= 0,137, как обеспечивающее восстановление позиций по обоим показателям.
Следует заметить, что абсолютные величины найденных интенсивностей не имеют самостоятельного значения. При интерпретации полученных результатов необходимо обратить главное внимание на отношение интенсивностей
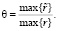(7)
В рассматриваемом примере данное отношение равно 2,91. Это означает, что для возвращения на усредненную расчетную траекторию по обоим показателям, интенсивность потока учебных проблем, подлежащих освоению, должна быть увеличена по сравнению с обычной ~2,9 раза. Такое высокое значение θ в данном примере объясняется фактом схода с траектории сразу по двум показателям, что для учебного процесса есть признак критической ситуации.
Заключение
1. Построена математическая модель на основе системы совместных регрессионных уравнений усредненного процесса развития способностей, предназначенная для использования в образовательных SMART-системах.
2. Разработан алгоритм оперативного управления процессом обучения в режиме реального времени.
3. Полученные результаты могут быть использованы как для разработки рабочих программ и усредненных траекторий развития способностей, так и для обеспечения эффективного индивидуализированного обучения.
Библиографическая ссылка
Обади А.А., Печеный Е.А., Нуриев Н.К. МАТЕМАТИЧЕСКИЕ МОДЕЛИ ПРОГНОЗА И ОПЕРАТИВНОГО УПРАВЛЕНИЯ РАЗВИТИЕМ МНОГОПАРАМЕТРИЧЕСКИХ ОБЪЕКТОВ // Современные наукоемкие технологии. – 2019. – № 8. – С. 55-60;URL: https://top-technologies.ru/ru/article/view?id=37630 (дата обращения: 19.04.2024).