В современных системах связи широко используются турбокоды, среди которых можно выделить коды Хэмминга и Рида – Соломона [1–3]. Это связано с тем, что турбокоды обладают хорошими корректирующими характеристиками. Они способны исправлять пачки ошибок, вызванные помехами в канале связи. Однако эти коды не могут исправлять ошибки, возникающие в процессе вычислений из-за отказа и сбоев оборудования. При этом известные арифметические модулярные коды (МК) – коды системы остаточных классов (СОК), которые могут исправлять ошибки вычислений, не используются в качестве помехоустойчивых кодов. Это связано со значительными схемными затратами, необходимыми для борьбы с пачками ошибок. Устранить данный недостаток возможно за счет применения алгоритмов реализации турбокодов к кодам СОК. Поэтому разработка новых принципов построения турбокодов на основе МК является актуальной задачей.
Современные модулярные коды нашли широкое применение при построении отказоустойчивых спецпроцессоров (СП) цифровой обработки сигналов (ЦОС). Так, используя два контрольных основания, коды СОК способны корректировать однократные ошибки, возникающие из-за отказов и сбоев в процессе вычислений [4]. Однако такой избыточности недостаточно, чтобы обеспечить требуемую помехоустойчивость системы передачи данных. Это связано с тем, что ошибки в каналах связи группируются в пачки. Для обнаружения и коррекции пачек ошибок в коде СОК необходимо увеличивать количество избыточных оснований, что негативно сказывается на схемных затратах СП ЦОС. Устранить данный недостаток возможно за счет реализации кодов СОК в виде турбокодов [5]. Поэтому целью статьи является повышение корректирующих способностей кодов СОК за счет применения алгоритмов построения турбокодов.
Материалы и методы исследования
Код СОК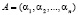 
представляет собой набор остатков, которые получаются при делении целого числа А на взаимно простые основания p1, p2,..., pn. Такой набор оснований кода СОК задает рабочий диапазон
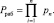(1)
Так как каждый остаток несет информацию о числе А, то это позволяет осуществлять параллельную обработку кодовых комбинаций. Так как в коде СОК отсутствует обмен данными между остатками, то данное свойство используют для поиска и коррекции ошибок. Согласно [4] для коррекции однократной ошибки вводятся два контрольных основания, удовлетворяющие условию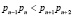 
. В результате получается полный диапазон
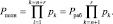(2)
Заданной системе оснований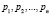 
соответствует система ортогональных базисов B1, B2,..., Bn, с помощью которых осуществляется перевод в позиционный код:
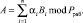(3)
Из [6, 7] известно, что комбинация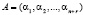 
считается разрешенной, если
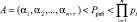. (4)
Если ошибка произошла по i-му основанию кода СОК, то комбинация равна
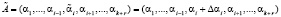. (5)
где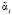 
– искаженный остаток кода СОК, ?αi – глубина ошибки по i-му основанию.
Для оценки эффективности разработанного алгоритма построения модулярных турбокодов, произведем сравнение классического подхода построения МК (рис. 1) с турбокодом, использующим в качестве компонентных кодов МК (рис. 2).
Рис. 1. Классический подход построения модулярных кодов
Рис. 2. Турбокод, построенный на базе модулярных кодов
В обоих случаях при кодировании вводится по r = 2 контрольных основания ввиду того, что поток отказов является простейшим, поэтому для исправления однократной ошибки (в одном остатке) достаточно введения двух контрольных оснований [7, 8]. Поэтому комбинация при трех информационных основаниях имеет вид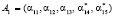 
, где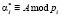 
, i = n + 1, n + 2. Тогда для других двух комбинаций справедливо
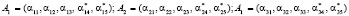. (6)
Для повышения корректирующих способностей такого кода вводятся два избыточных основания удовлетворяющих условию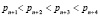 
. Это приводит к получению полного диапазона 
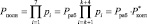. В результате второй итерации имеем
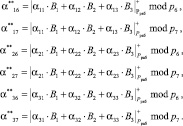(7)
В этом случае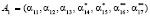 
; 
; 
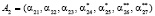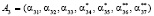. Эти комбинации МК способны исправлять двукратные ошибки. Пусть при передаче по каналу связи в первой комбинации А1 исказились остатк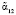и 
и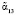 
, а глубина ошибок равна ?α12 и ?α13. Тогда справедливо
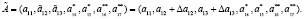(8)
При переводе в позиционную систему счисления [5] получим
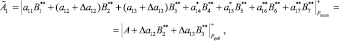(9)
где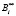 
– ортогональный базис полной системы оснований СОК; i = 1,…,7.
Очевидно, что из-за ошибки А1 находится вне рабочего диапазона. Для коррекции искаженных остатков воспользуемся позиционной характеристикой интервальным номером
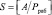, (10)
где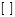 
– целая часть при делении числа А на рабочий диапазон.
Согласно [7], если МК не содержит ошибки, то S = 0. В противном случае по значению интервального номера можно определить искаженные ошибки и глубину ошибки.
В разработанном алгоритме построения турбокодов на базе МК используются только два контрольных основания. В результате получаем три комбинации следующего вида
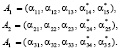(11)
Вычислим дополнительные проверочные символы согласно
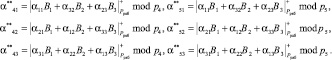(12)
Анализ (12) показывает, что для получения проверочных остатков использовались информационные вычеты из разных комбинаций. Тогда модулярный турбокод имеет вид
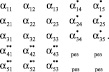(13)
Пусть из-за помехи исказились остатки α12 и α13. Тогда турбокод СОК имеет вид
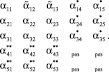(14)
В разработанном алгоритме сначала производится вычисление интервального номера построчно. В результате для первой комбинации получаем
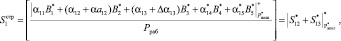(15)
где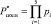 
; 
; 
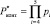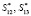– интервалы, в которые попадает МК при ошибках 
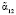и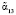 
с глубиной ?α12, ?α13 соответственно; 
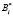– ортогональный базис СОК; i = 1,…,5.
При наличии двух контрольных оснований pn+1 и pn+2 код СОК не сможет однозначно определить ошибочные остатк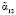и 
и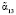 
и глубину ошибок ?α12 и ?α13. Поэтому проводим вычисления других интервалов с использованием дополнительных остатков. Тогда
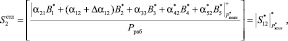(16)
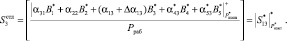(17)
При выполнении (16) и (17) декодер модулярного турбокода однозначно определит ошибочные остатк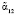и 
и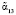 
, а также их глубину ?α12 и ?α13. Для проверки производится суммирование вычисленных интервальных номеров. В результате получаем
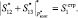(18)
Полученное равенство свидетельствует о том, что результаты, полученные при вертикальных проверках, обнаружили ошибочные остатк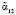и 
и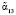 
и определили их глубину. Тогда исправленное значение комбинации определяется
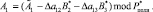(19)
При этом для коррекции пачки ошибок декодеру модулярного турбокода достаточно запомнить интервальных номеров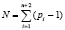 
. Благодаря этому модулярный турбокод может исправлять и трехкратные ошибки. Пусть из-за помехи исказились остатк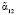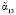и 
, 
и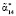 
. В результате этого при построчной проверке будет получено значение
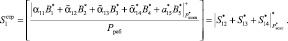(20)
При проведении вертикальных проверок будут получены значения интервальных номеров согласно (16) и (17). Затем декодер турбокода вычисляет
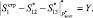(21)
Так как значение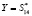 
совпадает с интервальным номером ошибочного основания 
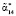, которое хранится в памяти декодера турбокода, то исправленный код имеет вид
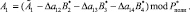(22)
Значит, используя два контрольных основания модулярный турбокод смог исправить пачки ошибок более высокой кратности.
Результаты исследования и их обсуждение
Для оценки эффективности предложенных решений по построению турбокодов СОК был разработан программный комплекс, имитирующий канал связи под воздействием импульсных помех различной длительности, который позволяет провести до 232 независимых экспериментов [9]. С использованием данного программного комплекса, были проведены 10 000 экспериментов. Были заданы вероятности возникновения импульсных помех, искажающих биты комбинаций, затрагивающих одно, два, три основания. В качестве информационных оснований были выбраны модули вида 2m – 1, 2m, 2m + 1. При m = 5 получаем р1 = 31, р2 = 32, р3 = 33. Рабочий диапазон равен Рраб = 32736. В качестве избыточных оснований для турбокода были выбраны р4 = 37, р5 = 41. В результате полный диапазон турбокода составляет Р*полн = 49660512. Для классического алгоритма исправления двукратных ошибок были выбраны еще два контрольных основания р6 = 43, р7 = 41. Тогда полный диапазон кода СОК с четырьмя контрольными модулями равен Р*полн = 100363894752. Вероятность исправления ошибок P рассчитывалась как частное от количества ошибочных кодовых комбинаций Nиспр, которые декодер может исправить, на общее количество ошибок Nош, т.е. Р = Nиспр / Nош. Результат проведенных исследований эффективности разработанного алгоритма построения модулярного турбокода приведен на рис. 3.
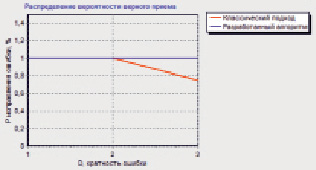
Рис. 3. Распределение вероятности верного декодирования МК
Проведенный анализ показывает, что при возникновении однократных и двукратных ошибок модулярные коды исправляют 100 % ошибочных комбинаций. При увеличении кратности ошибок классический МК может исправить 75,2 % трехкратных ошибок, а разработанный модулярный турбокод обеспечивает 100 % коррекцию данных пачек ошибок. При этом при использовании разработанного модулярного турбокода сокращаются схемные затраты. Так для выбранных информационных и проверочных модулей разрядность обрабатываемых данных составляет 39 разрядов. А при использовании разработанного модулярного турбокода разрядность равна 27 разрядам, что в 1,44 раза меньше.
Заключение
В статье показана актуальность разработки турбокодов на основе кодов СОК. Представлен алгоритм построения модулярного турбокода с двумя контрольными основаниями. Рассмотрены процессы поиска и коррекции пачки ошибок в разработанном модулярном коде. Используя разработанный программный комплекс, были проведены исследования корректирующих способностей модулярного турбокода. Полученные результаты показали, что при возникновении однократных и двукратных ошибок модулярные коды исправляют 100 % ошибочных комбинаций. При увеличении кратности ошибок классический МК может исправить 75,2 % трехкратных ошибок, а разработанный модулярный турбокод обеспечивает 100 % коррекцию данных пачек ошибок. Кроме того, при использовании разработанного модулярного турбокода также сокращаются схемные затраты. Так для выбранных информационных и четырех проверочных модулей разрядность обрабатываемых данных составляет 39 разрядов. А при использовании разработанного модулярного турбокода разрядность равна 27 разрядам, что в 1,44 раза меньше.
Исследование выполнено при финансовой поддержке РФФИ в рамках научного проекта № 18-07-01020.
Библиографическая ссылка
Калмыков И.А., Ефременков И.Д., Юрданов Д.В., Волошин Е.А., Проворнов И.А. РАЗРАБОТКА АЛГОРИТМА ПОСТРОЕНИЯ ТУРБОКОДОВ НА ОСНОВЕ МОДУЛЯРНЫХ КОДОВ // Современные наукоемкие технологии. – 2019. – № 8. – С. 43-48;URL: https://top-technologies.ru/ru/article/view?id=37628 (дата обращения: 23.11.2024).