В работе [1] рассматриваются математические модели одиночных эмоций робота, являющихся аналогами эмоций человека. Данная теория может быть использована, например, маркетологами в оценке эмоционального влияния продуктов масс-медиа, владельцами колл-центров для предотвращения соединения разозленного клиента с работниками. Также в работе [1] рассматривается теория комплексных эмоций роботов. В работе [2] рассматриваются математические модели амбивалентных эмоций робота, аналогичных эмоциям человека, которые описывают одновременное появление эмоций разного знака и могут использоваться, например, для моделирования реакций человека в определенных эмоциональных ситуациях. Эмоциональная амбивалентность – это внутренне противоречивое эмоциональное состояние или переживание, которое связано с двойственным отношением к человеку, предмету, явлению и которое человек одновременно и принимает, и отвергает [3]. Отметим, что амбивалентные эмоции являются вектором состоящим из двух эмоций:
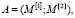
где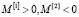 
. Недостаток публикаций [1, 2] состоит в том, что понятие комплексных эмоций не раскрывается в достаточной мере. Поэтому в [4] предложена математическая модель комплексных эмоций робота. Рассмотрим свойства комплексных эмоций, комплексных элементарных воспитаний и комплексных воспитаний робота.
Комплексные эмоции и комплексные воспитания робота
Выдвинем гипотезу, говорящую о том, что в ответ на любой сюжет-стимул у робота всегда возникает комплексная эмоция. Настоящая статья посвящена изучению свойств комплексных эмоций робота на основе теории линейных пространств [5, 6].
Будем предполагать, что вектор комплексной эмоции представим в виде
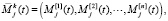
(где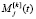 
– базовая эмоция робота, аналогичная базовой эмоции человека, [k] – порядковый номер базовой эмоции, j – номер такта, 
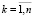) и удовлетворяют следующим допущениям:
1. Базовые эмоции можно измерять по одной и той же шкале.
2. Базовые эмоции можно складывать и умножать. Сложение и умножение базовых эмоций можно определить следующим образом: cложение и умножение эмоций определяет законы зависимости каждой базовой эмоции друг от друга, то есть выдвигаем гипотезу о том, что базовые эмоции зависят друг от друга.
3. Базовые эмоции можно умножать на число.
4. Существует безэмоциональное состояние робота, соответствующее всем нулевым базовым эмоциям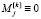 
, 
.
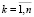5. Продолжительность каждой базовой эмоции одинакова, иными словами, величины тактов каждой базовой эмоции равны между собой.
Отметим то, что вещественные функции f(t), определенные на отрезке [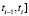
и удовлетворяющие условию 
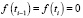, где 
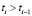удовлетворяют этим допущениям. Сумма и произведение функций g(t) и x(t), удовлетворяющие свойствам 
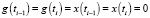, являются функциями такого же вида что и f(t), 
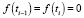. Значит, функции f(t) образуют поле.
Так как по определению эмоции [1] удовлетворяют свойству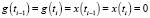 
, то мы можем говорить о линейном пространстве эмоций над полем функций изоморфном пространству вектор-строк размерности n. Значит, для этого пространства комплексных эмоций можно сформулировать следующие теоремы:
1. В линейном пространстве M существует единственный нулевой элемент. То есть в пространстве M нулевому элементу соответствует безэмоциональное состояние робота.
2. Для каждого элемента существует единственный противоположный элемент. В нашем случае для каждой базовой эмоции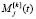 
существует базовая эмо- ция 
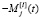которую можно назвать противоположной базовой эмоцией. Комплексную эмоцию, составленную из базовых эмоций, противоположных данным, будем называть противоположной комплексной эмоцией.
3. При сложении двух любых элементов линейного пространства M их координаты складываются; при умножении произвольного элемента на любое число λ все координаты этого элемента умножаются на λ [5].
4. Линейная комбинации комплексных эмоций является комплексной эмоцией. Доказательство очевидно следует из теоремы 3 и свойства функции:
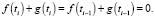
Каждый элемент суммы является базовой эмоцией в смысле приведенном выше.
5. Совокупность линейно независимых элементов e1, e2,?, en пространства M назовем базисом этого пространства, если для каждого элемента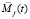 
пространства M найдутся вещественные функции от параметра «время» 
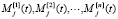, такие, что справедливо равенство
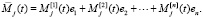
Разложение по базису единственно.
6. Если M – линейное пространство размерности n, то любые n линейно независимых элементов этого пространства образуют его базис.
7. Если линейное пространство M имеет базис, состоящий из n элементов, то размерность M равна n.
Рассмотрим элементарное воспитание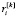 
от базовой эмоции 
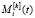. Оно принимает вид 
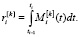Соответственно, воспитание от базовой эмоции 
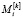в ви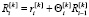де 
, где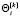 
коэффициент памяти робота, для базовой эмоции с номером [k], 
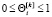представленные в работе [1].
Предположим, что базовые эмоции одного типа порождают элементарные воспитания одного типа. Тогда мы можем рассмотреть вектора комплексных элементарных воспитаний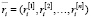 
и комплексных воспитаний 
.
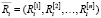Пусть z(t) и y(t) базовые эмоции. И пусть φ(t) = z(t) + y(t), тогда очевидно соотношение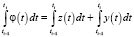 
которое позволяет утверждать, что элементарное воспитание суммы равно сумме элементарных воспитаний от базовой эмоции. Предполагая, что 
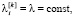можно сформулировать следующее утверждение. Если z(t) = λy(t), то элементарное воспитание произведение равно 
.
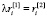Таким образом пространство комплексных элементарных воспитаний изоморфно [5] пространству эмоций. Отсюда следует, что теоремы 1–7 справедливы и для пространства комплексных элементарных воспитаний. Безэмоциональное состояние формирует нулевое воспитание. Линейно независимая комбинация комплексных эмоций будет соответствовать линейно независимой комбинации элементарных воспитаний.
Гармонические эмоции и гармонические воспитания робота
В работе [1] описывается элементарная эмоция в виде гармонической функции.
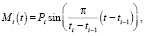
где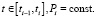 
Пусть λ = λ(t).
Теорема 1
Для гармонических амбивалентных эмоций λ(t) = const.
Доказательство
Докажем теорему методом «от противного».
Предположим, что λ(t) ≠ const, тогда выполняется равенство
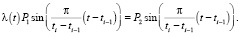
Поскольку P1, P2 и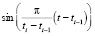 
не равны тождественно нулю, то справедливо соотношение
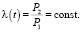
Последнее равенство, противоречащее исходному предположению, и доказывает теорему.
Предположим, что для всех базовых эмоций ti – ti-1 = const. Тогда сумма двух базовых эмоций будет являться базовой эмоцией. Докажем это утверждение. Справедлива цепочка равенств
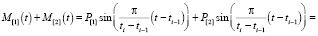
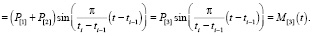
Если мы умножим базовую эмоцию на число, то получим базовую эмоцию. Докажем следующую теорему.
Теорема 2
Произведение базовой эмоции на число является базовой эмоцией.
Доказательство
Очевидна цепочка равенств:
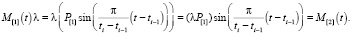
Таким образом, теорема доказана.
Очевидно, что безэмоциональное состояние достигается в том случае, если P = 0.
Для каждой базовой эмоции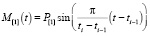 
базовая эмоция 
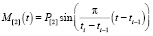будет противоположной, если P[2] = –P[1]. Вышеперечисленные свойства дают возможность представлять комплексную эмоцию в виде линейной комбинации других комплексных эмоций.
Естественным базисом будет набор комплексных эмоций
...
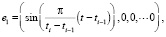
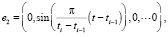
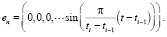
Каждая комплексная эмоция этого базиса соответствует воздействию одной базовой эмоции «стандартного уровня», т.е. при P = 1.
Одним из базисов в пространстве комплексных элементарных воспитаний, порожденных гармоническим эмоциями, будут элементарные воспитания, сформированные базовыми гармоническими эмоциями:
...
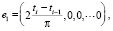
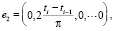
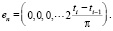
Предположим, что коэффициент памяти робота является постоянным для всех воспитаний, порожденных одним типом элементарных воспитаний, т.е.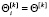 
. Поскольку формула воспитания 
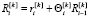задает однозначное соответствие между элементарными воспитаниями и воспитаниями (притом 
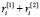соответствует 
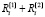), то пространство воспитаний изоморфно пространству элементарных воспитаний. Это дает нам возможность применять теоремы 1–7 для описания свойств воспитаний.
Таким образом, можно перечислить следующие общие свойства математических моделей комплексных эмоций робота:
1. Комплексные эмоции удовлетворяют свойствам изоморфизма линейных пространств.
2. Любую комплексную эмоцию можно представить как линейную комбинацию базиса, описывающего базовые эмоции.
3. Гармоническую комплексную эмоцию можно представить как линейную комбинацию базисных гармонических эмоций, имеющих вид
...
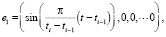
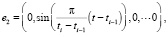
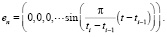
Аналогично можно перечислить общие свойства математических моделей воспитаний и элементарных воспитаний:
1. Воспитания и элементарные воспитания удовлетворяют свойствам изоморфизма линейных пространств.
2. Воспитания можно представить как линейную комбинацию базиса воспитаний.
3. Элементарные воспитания можно представить как линейную комбинацию базиса элементарных воспитаний.
Заключение
Таким образом, в статье адаптированы теоремы о базисе линейных пространств к представлению комплексных эмоций и комплексных воспитаний робота, предложен вид базиса линейных пространств гармонических комплексных эмоций и гармонических комплексных воспитаний робота, приведены примеры представления гармонических комплексных эмоций и воспитаний через эти базисы.
Согласно гипотезе, сформулированной в настоящей статье и говорящей о том, что на любой стимул-раздражитель в ответ возникает не одна базовая эмоция, а комплексная эмоция, возможно более адекватное описание поведения робота при встрече с неизвестным объектом. При этом эмоциональные роботы с комплексными эмоциями могут быть использованы в системах принятия решений.
Предлагаемая адаптация теорем имеет широкую область практического применения. Эмоции показывают окружающим внутреннее состояние человека и его реакцию на определенные ситуации. На одни и те же ситуации люди реагируют по-разному, а эмоции помогают определить реакцию. Роботы с комплексными эмоциями, на наш взгляд, смогут более реалистично представлять реакцию на разные ситуации.
Отметим то, что адаптированные теоремы линейных пространств к описанию комплексных эмоций позволяют описывать более частный случай реакции на внешние стимулы – амбивалентные эмоции робота.
В качестве одного из аналогов психологии поведения живых существ можно использовать робота с гармоническими комплексными эмоциями, описанными в настоящей статье. Согласно предложенным теоремам, адаптированным к такого типа эмоциям, и предложенному базису пространства комплексных гармонических эмоций можно описать любую комплексную гармоническую и амбивалентную гармоническую эмоцию робота как линейную комбинацию базовых гармонических эмоций. Это позволит, на наш взгляд, без большого труда компьютеризировать эмоциональное поведение робота, являющегося аналогом живого существа.
Библиографическая ссылка
Анисимова С.И. ОБЩИЕ СВОЙСТВА МАТЕМАТИЧЕСКИХ МОДЕЛЕЙ КОМПЛЕКСНЫХ ЭМОЦИЙ РОБОТА // Современные наукоемкие технологии. – 2019. – № 8. – С. 9-13;URL: https://top-technologies.ru/ru/article/view?id=37622 (дата обращения: 21.11.2024).