Предоставление педагогам инструментов диагностики и преодоления индивидуальных пробелов в обучении математике – одна из задач, поставленных Концепцией развития математического образования в Российской Федерации [1]. Реализация высшего образования предполагает проведение диагностики в процессе обучения математике студентов вуза. Анализ существующей практики педагогической диагностики математической подготовки студентов показал, с одной стороны, необходимость ее эффективной организации, а с другой – недостаточность средств ее реализации. В современной системе образования широко используется портфолио, в том числе и для педагогической диагностики. В сфере высшего образования портфолио рассматривается как средство оценки сформированности компетенций [2] и как технология развития профессиональных и личностных качеств студентов [3].
Цель исследования: разработать и экспериментально проверить модель диагностики математической компетентности студентов экономических направлений на основе портфолио путем анализа диагностируемого феномена и установления соответствия средств и методов диагностики структуре математической компетентности.
Материалы и методы исследования
В основу нашего исследования положен метод моделирования для построения структурно-функциональной модели диагностики на основе портфолио и математической модели преобразования исходных диагностических данных в искомый показатель.
Результатом математической подготовки бакалавров экономических направлений мы полагаем их математическую компетентность. Структура математической компетентности отражает структуру математической деятельности, включая три основные части, каждая из которых конкретизируется соответствующим перечнем компетенций (рис. 1).
Рис. 1. Структура математической компетентности
Компетенции, входящие в первую и вторую части математической компетентности, конкретизированы следующим образом (рис. 2), а конкретизация компетенции из третьей части связана с содержанием изучаемого материала и далее будет показана на примере темы «Интегральное исчисление».
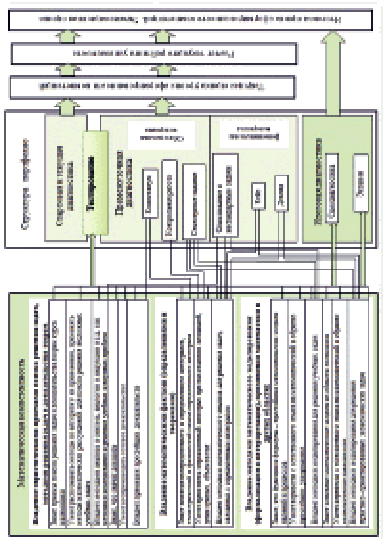
Рис. 2. Структура портфолио для диагностики математической подготовки студентов
Сопоставление конкретизированных требований к математической подготовке студентов с существующими в теории и практике средствами и методами диагностики позволило выявить входящие в структуру портфолио методы и средства. Все элементы математической компетентности диагностировались с помощью тестирования во время стартовой, текущей и промежуточной диагностики, на экзамене в ходе итоговой диагностики и являлись предметом самодиагностики. Коллоквиум служил для диагностики знания теоретического материала и владения приемами доказательств, а контрольная работа оценивала умение решать типовые задачи с помощью определенного интеграла. Семестровое задание направлено на диагностику умения применять определенный интеграл и владение методами моделирования. Олимпиадные и нестандартные задачи, например вычислить интеграл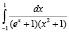 
, позволяют оценить владение эвристическими приемами поиска решения задач, связанных с определенным. Кейс и доклад проверяют владение методами математического анализа и методами моделирования для решения практико- ориентированных экономических задач [4].
Опишем разработку содержательного наполнения модели на примере компетенции «Владение способностью составлять математические модели практико-ориентированных задач, находить способы их решений и интерпретировать практический смысл полученного математического результата» на примере темы «Интегральное исчисление». Знание основных математических моделей из области экономики проверяет следующее тестовое задание:
По какой формуле вычисляется производительность труда p(t), если A(t) – объем работы, выполненный на момент времени t?
1. p(t) = A'(t).
2. 
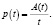
3. 
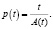
4. p(t) = A(t)?t.
Примером тестового задания для диагностики умения перевести с естественного языка на математический и обратно экономические зависимости является следующее:
Объем выпуска продукции предприятия в 2010 г. составлял 100000 единиц, и в каждом последующем году увеличивался на 10000 единиц. Себестоимость одной единицы продукции – 340 р., а норма амортизации равнялась 1,25 % от себестоимости продукции. Найдите сумму амортизационных отчислений с 2010 по 2019 г.
1. 
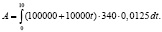
2. 
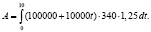
3. A = ∫ (100000 + 10000t)dt?340?0,0125 dt + C.
4. A = (100000 + 10000?10)?340?0,0125.
Одно из семестровых заданий по теме «Интегральное исчисление» содержало прикладную задачу: «Поступление товара на склад описывается функцией V = 0,006t2 – 0,3t + 75, а реализация этих товаров торгующей организацией описывается функцией V1 = 0,003t2 – 0,4t + 56, где t – количество дней. Определить запас товара в условных единицах по истечении 60 рабочих дней, если исходного товара на складе не было», диагностирующую знание основных математических моделей из области экономики и владение методами моделирования для решения практико-ориентированных экономических задач. В качестве кейса студентам предлагалось задание: первоначальное капиталовложение составляет 20 млн руб., планируется ежегодно увеличивать капитал на 6 млн руб. Определите дисконтированный доход за пять лет при процентной ставке 10,5 %. Раскройте экономический смысл полученного результата.
Опишем составление математической модели [5] для диагностики вышеуказанной компетенции. В тесте, диагностирующем знание основных математических моделей из области экономики и умение перевести с естественного языка на математический и обратно экономические зависимости, каждое тестовое задание оценивалось одним баллом и коэффициенты сформированности компетенции на уровне знания и умения вычислялись как процент верно выполненных заданий. Владение методами моделирования для решения практико-ориентированных экономических задач также оценивалось с помощью теста (каждое тестовое задание по 1 баллу), семестрового задания (каждая задача по 2 балла), доклада и кейса (каждый оценивался по 3 балла), и коэффициент сформированности компетенции на уровне владения вычислялся как процент набранных баллов от их максимальной суммы.
Для построения математической модели мы использовали метод наименьших квадратов, позволивщий построить эмпирическое уравнение регрессии y = 3,29 + 0,30x1 + 0,23x2 + 0,44x3, где x1, x2, x3 – коэффициенты сформированности компетенций студента (по стобалльной шкале) на соответственно уровнях «знать», «уметь», «владеть». Полученное уравнение позволяет диагностировать текущее состояние сформированности компетенции в каждый момент времени. Это позволяет организовать коррекционную работу для ликвидации пробелов и недочетов, а также стимулировать студентов к улучшению своей математической подготовки. По каждой компетенции была построена своя математическая модель, учитывающая результаты всех контрольных мероприятий, затем вычислялось среднее значение коэффициента сформированности компетенций. В конце изучения дисциплины формировалась итоговая оценка сформированности компетенций, которая затем преобразовывалась в экзаменационную оценку.
В ходе итоговой самодиагностики студент должен был оценить свою деятельность по освоению дисциплины, выставив себе оценку, которую можно подтвердить теми или иными составляющими портфолио. После того, как все достижения были задокументированы, студенты просматривали свое портфолио и заполняли карту самооценки, в которой оценивали сформированность собственных компетенций и в свободной форме описывали положительные и отрицательные моменты своей учебной деятельности при изучении дисциплины, отмечали лучшие свои работы (рис. 3). Например, студентка Мария И. пишет, что в процессе изучения темы «Интегрирование функций одной переменной» она узнала, что многие явления и процессы экономики описываются с помощью определенного интеграла, научилась применять интеграл для вычисления объёма продукции, произведенный за данный промежуток времени, приращения капитала по объему инвестиций, величины банковского вклада по его начальной величине и процентной ставке, добавочной выгоды (излишка) производителя и потребителя. Аргументированное заполнение карты самооценки позволяло студенту повысить свою итоговую оценку.
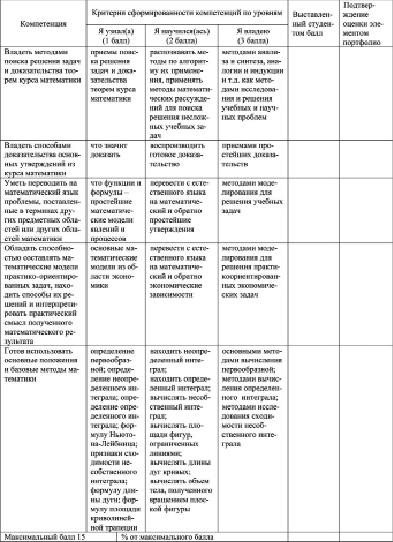
Рис. 3. Карта самооценки студента
Результаты исследования и их обсуждение
Анализ эффективности диагностики математической подготовки студентов на основе портфолио проводился в процессе опытно-поисковой работы на факультете экономики и управления Южно-Уральского государственного университета в 2012–2019 гг. по показателям сформированности мотивации, умений самодиагностики студентов и качества информации, полученной с помощью портфолио, о сформированности у них математических компетенций.
Уровень мотивации студентов оценивался с помощью методики «Определение уровня мотивации достижения успеха» [6]. Мы выделили три группы исследуемых: характеризующихся мотивом стремления к успеху (высокий уровень), характеризующихся мотивом избегания неудачи (низкий уровень), составляющих средний уровень. Уровень рефлексивности оценивался по методике А.В. Карпова [7]. Результаты опытно-поисковой работы представлены в таблице.
Динамика уровня сформированности мотивации и рефлексивности
|
Уровень сформированности мотивации |
Уровень рефлексивности |
|||
|
До начала опытно- поисковой работы |
После опытно- поисковой работы |
До начала опытно- поисковой работы |
После опытно- поисковой работы |
|
|
высокий |
15 |
25 |
13 |
28 |
|
средний |
35 |
48 |
36 |
47 |
|
низкий |
94 |
71 |
95 |
69 |
|
Всего |
144 |
144 |
144 |
144 |
По обоим показателям значение критерия Пирсона χ2эксп больше χ2кр, значит, изменение уровней сформированности мотивации и рефлексии, обусловленное реализацией модели педагогической диагностики математической подготовки на основе портфолио, является достоверным.
Качество информации о сформированности у студентов математической компетентности мы определяем как степень соответствия результатов диагностики с помощью портфолио экспертным оценкам. Ранговый коэффициент корреляции К. Спирмена этих двух рядов оценок для группы из 40 студентов составил 0,56, что превышает критическое значение 0,40 на уровне значимости 0,01. Таким образом, результаты диагностики математической компетентности студентов на основе портфолио коррелируют с результатами экспертной оценки, что свидетельствует о качестве диагностической информации.
Выводы
Выявив структуру математической компетентности студентов экономических направлений, мы разработали структуру портфолио, включающую стартовую, текущую, промежуточную и итоговую диагностику. Разработанная модель диагностики на основе портфолио устанавливает взаимосвязь компетенций, конкретизирующих математическую компетентность, и элементов портфолио. Содержательное наполнение модели реализует соответствие математических компетенций и средств и методов их диагностики.
На основе регрессионного анализа была построена математическая модель для количественной оценки компетенций, суммирующая результаты всех контрольных мероприятий, определяющих структуру портфолио. Экспериментальная проверка построенной модели позволила судить о ее эффективности как соответствии критериям сформированности мотивации, умений самодиагностики и качеству информации о процессе и результатах математической подготовки студентов.
Библиографическая ссылка
Суховиенко Е.А., Абдрахимова Д.И. МОДЕЛЬ ДИАГНОСТИКИ МАТЕМАТИЧЕСКОЙ КОМПЕТЕНТНОСТИ СТУДЕНТОВ ЭКОНОМИЧЕСКИХ НАПРАВЛЕНИЙ НА ОСНОВЕ ПОРТФОЛИО // Современные наукоемкие технологии. – 2019. – № 7. – С. 224-229;URL: https://top-technologies.ru/ru/article/view?id=37618 (дата обращения: 18.04.2024).