Очевидно, процесс развития проектно-конструктивных способностей человека зависит от сотен взаимосвязанных факторов. Этот процесс является латентным и происходит в когнитивной сфере человека, поэтому не поддается никаким непосредственным измерениям и наблюдениям. В то же время задача управления процессом развития проектно-конструктивных способностей человека, на основе каких-то воздействий, остается актуальной проблемой для многих наук.
В процессе развития проектно-конструктивных способностей можно выделить интегративные характеристики. На практике под интегративной характеристикой понимается сложная характеристика, которая не сводится только к сумме ее составляющих. В целом при моделировании систем и процессов, использование интегративных характеристик представляет собой способ понижения размерности системы, который позволяет решить проблему «проклятия размерности» для больших и сложных систем. Таким образом, в модели интегративная характеристика – это переменная, представляющая собой множество переменных, находящихся ниже в иерархической структуре организации системы. В самоорганизующихся и саморазвивающихся системах со сложной структурой подсистем этот параметр несет интегрированную информацию о поведении этих подсистем, по которым можно судить о поведении всей системы в целом [1, 2].
Цель исследования: разработка математической модели развития проектно-конструктивных способностей в деятельности для построения цифровых технологий с целью их использования в автоматизированных SMART-системах.
Материалы и методы исследования
Рассмотрим процесс решения человеком проблемы сложности S через его деятельность. Особо отметим, что все люди решают проблему одним и тем же способом:
1. На основе своих знаний человек формализует проблему в когнитивной сфере и, сняв множество неопределенностей, трансформирует ее в задачу.
2. Так же, на основе своих знаний, человек конструирует план решения этой задачи.
3. И, наконец, на основе своих знаний и с привлечением других ресурсов человек исполняет этот план в какой-то среде (реальной, виртуальной).
Таким образом, в общем процессе можно выделить три операции: формализация проблемы, конструирование плана, исполнение плана, которые следуют друг за другом со своими интегративными характеристиками. Эти интегративные взаимосвязанные характеристики обозначим соответственно через A, B, C. В рамках методологии SADT весь процесс решения человеком проблемы в модели может быть представлен как функционирующая система, которая трансформирует проблему в результат (рис. 1). В этой модели интегративные характеристики представлены параметрами: A, B, C, POL, CHL, S.
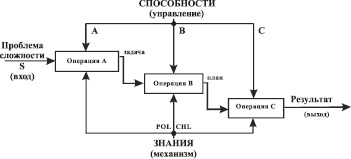
Рис. 1. Диаграмма трансформации человеком проблемы в результат
Через A, B, C соответственно обозначены формализационные, конструктивные, исполнительские способности человека, решающего проблему. Интегративные параметры POL, CHL характеризуют качество сформированности базы знаний человека с двух точек зрения: с точки зрения его информативной полноты, относительно решаемой проблемы и его конструктивной целостности. Параметр S – сложность проблемы, также является интегративным параметром. С субъективной точки зрения человека, решающего проблему, сложность этой проблемы формируется из трудностей SA, SB, SC, т.е. трудностей формализации проблемы, конструирования плана решения задачи, исполнения этого плана на практике [2].
Коротко (на принципиальном уровне), трансформация человеком проблемы в результат проходит следующим образом. Проблема сложности S на фоне его знаний трансформируется (через способность типа А) в задачу; задача на фоне знаний трансформируется (через способность типа В) в план решения задачи; план на фоне знаний и на основе других ресурсов трансформируется (через способность типа С) в результат. При этом, очевидно, каждый человек на актуальный момент времени имеет определенный уровень развития проектно-конструктивных, т.е. ABC способностей и качество сформированности системы своих знаний. Разумеется, чем выше уровень развития A, B, C способностей, и качество сформированности знаний (значение параметров POL, CHL), тем больше у него значение вероятности P(пол) положительно разрешить проблему сложности S. Формально, на принципиальном уровне, это значение вероятности при фиксированном значении S, может быть вычислено как значение функционала
P(пол) = F(A, B, C, POL, CHL, S). (1)
Таким образом, комплекс взаимосвязанных интегративных параметров POT = (A, B, C, POL, CHL) на актуальный момент времени определяет деятельностный потенциал человека, т.е. на вербальном уровне можно утверждать, что если POT больше S, то вероятность решить проблему велика [1, 2].
Эскизный проект развития ABC способностей на фоне знаний
В целом развитие ABC способностей на фоне системы знаний человека можно представить как процесс развития в пятимерном фазовом пространстве, принадлежащий когнитивной сфере этого человека. Фазовое пространство построено на пучке векторов A, B, C, POL, CHL (в строгом смысле, фазовое пространство будет псевдофазовым с учетом того, что эти вектора зависимые и не ортогональные). В этом фазовом пространстве (в дальнейшем мы не будем придерживаться этого строгого смысла) текущий деятельностный потенциал человека является целостной организацией и представлен в виде пентагона с конкретными значениями характеристических параметров: A = a, B = b, C = c, POL = pol, CHL = chl. В этом же фазовом пространстве, текущая проблема сложности SA = sa, SB = sb, SC = sc, также является целостной организацией, поэтому будет изображаться треугольником (рис. 2).
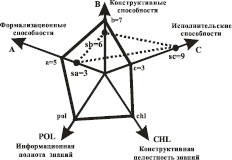
Рис. 2. Модель состояния развития ABC способностей на фоне знаний в фазовом пространстве
В динамике фазовая траектория развития проектно-конструктивных способностей человека будет состоять из цепочки деформирующихся пентагонов. То же самое происходит с траекторией потока проблем, т.е. поток будет состоять из цепочки деформирующихся, согласно их сложности, треугольников (рис. 3).
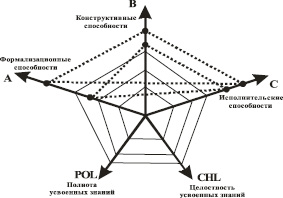
Рис. 3. Динамика развития деятельностного потенциала человека в его когнитивной сфере
Отыскания значения вероятности положительного решения человеком с определенным деятельностным потенциалом проблемы с определенной сложностью (рис. 2) предлагается вычислять как геометрические вероятности по формулам
P(RA) = (1, если а > sa или а/sa, если а < sa),
P(RB) = (1, если b > sb или b/sb, если b < sb),
P(RC) = (1, если c > sc или c/sc, если c < sc). (2)
Через RA, RB, RC обозначены случайные события и их вероятности P(RA), P(RB), P(RC) успешно завершить следующие операции: формализацию проблемы, конструирование плана решения, исполнение (реализацию) плана. Значение шанса успешно разрешить проблему в целом обозначено через Н (RA* RB*RC). Следует подчеркнуть, что шанс в рассматриваемом случае является оценкой вероятности, так как случайные события RA, RB, RC зависимы.
Н(RA*RB*RC) = P(RA) * P(RB) * P(RC) * KZ,
KZ = SQR(POL * CHL), (3)
где величина KZ – показатель качества знаний, который вычисляется как среднее геометрическое значения произведения POL * CHL.
Особо отметим, что переменные POL, CHL в вычислениях участвуют (значения их изменяется почти от 0 до 1), и они характеризуют проектно-конструктивный потенциал человека с точки зрения его знаний. В модели считается, что знания являются фоном (операционной средой) для развития АВС способностей и достигнутый уровень развития этих способностей уже предполагает KZ = 1. Это означает, что если человек при решении проблемы сложности (sa, sb, sc), с потенциалом (a, b, c) имеет P(RA) = 1 и P(RB) = 1 и P(RC) = 1, то у него KZ = 1, т.е. 100 % сформированные знания.
Рассмотрим пример, где в условных единицах заданы значения всех переменных, соответствующие ситуации на рис. 2, т.е. a = 5, sa = 3, b = 7, sb = 6, c = 3, sc = 9. Проведем вычисления и получим следующий результат: P(RA) = 1; P(RB) = 1; P(RC) = 1/3; KZ = 0,9; H(RA* RB*RC) = 1/3*0,9 = 0,3. Можно сделать вывод, что у человека, имеющего деятельностный потенциал (А = 5; В = 7; С = 3), шанс полностью решить проблему сложности (SA = 3; SB = 6; SC = 9) равен H(RA*PB*PC) = 30 % из возможных 100 %. Графическая интерпретация, рассмотренной ситуации приведена на рис. 2 [1, 2].
Математическая модель развития ABC способностей через учебную деятельность
Главной сложностью математического моделирования процесса обучения является то, что фактически основным его объектом выступает человек со всеми своими физическими, психологическими, социальными особенностями, сформированными под влиянием воспитания, окружающей среды и наследственных факторов. Законы, управляющие развитием личности человека, известны в настоящее время только на уровне понятий, этических и религиозных постулатов и никак не алгоритмизированы. Отсюда следует, что математическая модель учебного процесса может быть только моделью абстрактно-знакового типа [3], а в состав ее должны входить факторы допускающие количественные оценки, достоверность которых подтверждается результатами статистических наблюдений. Рассмотрим, каким требованиям должна удовлетворять упомянутая модель для того, чтобы быть содержательной и обладать необходимой полнотой.
Заметим прежде всего, что обучение как явление есть сложный многостадийный процесс, развернутый во времени, поэтому его математическая модель не может быть никакой иной кроме как динамической. Второе важное, на наш взгляд, обстоятельство – это форма контроля успеваемости (изменения ABC-способностей в ходе обучения). В автоматизированных обучающих системах, для управления которыми и предназначена разрабатываемая математическая модель, организация непрерывного контроля практически невозможна, а значит, время, как действующая переменная модели, должно быть дискретизировано и представлено в виде последовательности меток, связанных с контрольными точками (экзаменами, зачетами и т.п.).
Существенным для построения модели моментом является неразрывная связь ABC-способностей друг с другом в рамках каждой личности. Разумеется у различных людей преобладают разные способности, однако ни один тип способностей не может развиваться в совершенном отрыве от других. Известно и подтверждено многочисленными наблюдениями, что рост любого типа способностей подталкивает развитие остальных. К сожалению вид этой связи до настоящего времени остается неизвестным, а попытки ее количественной оценки не предпринимались. Разработанная математическая модель призвана указать возможный путь решения этой проблемы.
Как упоминалось выше, каждый человек обладает своим собственным спектром распределения способностей, а потому освоение компетенций и закрепление навыков у различных людей происходит по- разному. Поэтому, когда имеет место постоянное и непосредственное общение обучаемого и педагога, обучение есть сугубо индивидуальный процесс, предполагающий возможность особого подхода к каждому ученику. Построение математической модели такого процесса – задача непреодолимой сложности. Таким образом область применения разработанной модели ограничена только цифровыми автоматизированными системами обучения, в которых контакты между обучаемыми и педагогом происходят опосредованно и возможность учета индивидуальных особенностей обучаемых практически исключена. По этой причине в качестве переменных, входящих в состав модели, использовались усредненные величины ABC-способностей, определенные статистически по материалам достаточно представительных выборок в контрольных точках. Именно эти значения, связанные с соответствующими метками времени, формируют траектории процесса обучения
{At}; {Bt}; {Ct}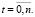 
Кроме высказанных замечаний при построении модели были приняты следующие гипотезы:
1. Начальный уровень способностей всех обучаемых предполагается не ниже некоторых пороговых значений, т.е.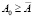 
; 
; 
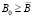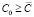. Это может быть обеспечено организацией должного входного контроля в форме экзаменационных испытаний, тестов и т.п.
2. Будем считать заданным уровень способностей, который должен быть достигнут по завершении процесса обучения A*; B*; C*. Он определяется рабочими программами изучаемых дисциплин и перечнем компетенций, подлежащих освоению. Естественно, что An ≥ A*; Bn ≥ B*; Cn ≥ C*.
3. Степень мотивации обучаемых предполагается высокой или, по крайней мере, достаточной для решения комплексов учебных проблем из зоны их ближайшего развития.
Результаты исследования и их обсуждение
В свете требований, сформулированных к модели и принятых гипотез, авторы сочли целесообразным выбрать для моделирования систему совместных регрессионных уравнений. В состав системы входят три уравнения по числу способностей, подлежащих развитию в ходе процесса обучения.
Структурная форма модели имеет вид
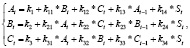(4)
где At – уровень формализаторских способностей в момент времени t; Bt – уровень конструктивных способностей в момент времени t; Ct – уровень исполнительских способностей в момент времени t; St – уровень сложности учебных проблем, предлагаемых обучающимся в момент времени t. В модели учтена взаимозависимость различных способностей друг от друга, связь текущего уровня способностей с предшествующими и введена переменная St, определяющая интенсивность обучающего воздействия и, по сути дела, играющая в модели роль управления. Подобные модели широко применяются в эконометрических исследованиях [4], потому в данной работе сохранена принятая там терминология и методические приемы.
Предлагаемая модель относится к классу идентифицируемых моделей, к чему, собственно, и стремились авторы, поскольку это открывает наиболее благоприятные возможности ее практического использования. Идентифицируемость устанавливается согласно счетному правилу идентификации для каждого уравнения системы в отдельности по соотношению
H = D + 1, (5)
где H – число эндогенных переменных, входящих в состав этого уравнения, т.е. таких переменных, которые имеются как в левых, так и в правых частях уравнений системы, в нашей модели это переменные At; Bt; Ct; D – число экзогенных переменных, имеющихся в составе уравнений модели, но отсутствующих в данном уравнении. К экзогенным относятся переменные, присутствующие только в правых частях уравнений. В данной модели это At-1; Bt-1; Ct-1; St.
В моделях такого типа наибольшую сложность представляет проблема идентификации – отыскания оценок параметров kij. Поскольку эндогенные переменные в разных уравнениях модели выступают в роли и зависимых и независимых, непосредственное применение процедуры метода наименьших квадратов для отыскания коэффициентов kij не позволяет получить их несмещенные оценки, что обесценивает результаты моделирования. Данное затруднение преодолевается с помощью косвенного метода наименьших квадратов. Алгоритм его довольно прост. Исходная модель преобразуется к приведенной форме, где все эндогенные переменные содержатся только в левых частях уравнений и зависят от одного и того же набора экзогенных переменных. Приведенная форма системы уравнений выполняет чисто вспомогательную функцию и самостоятельного значения не имеет. Коэффициенты приведенной формы находятся путем применения традиционного метода наименьших квадратов для каждого из уравнений приведенной формы системы в отдельности. Далее устанавливается функциональная связь между коэффициентами приведенной и структурной формы модели, с помощью которой определяются коэффициенты структурной формы. Известно [5, 6], что если структурная форма системы уравнений идентифицируема, то такая связь существует, хотя ее отыскание является отдельной и, как правило, непростой задачей, для решения которой не имеется универсальных рекомендаций. Рассмотрим последовательно все этапы реализации косвенного метода наименьших квадратов применительно к системе уравнений (4).
Прежде всего освободимся от свободных членов в уравнениях структурной формы k1, k2, k3, путем перехода к стандартизированным переменным
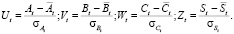(6)
Фактически эта операция эквивалентна процедуре нормирования, поскольку величины математических ожиданий новых переменных равны нулю, а среднеквадратичные отклонения – единице. Таким образом структурная форма модели для стандартизированных переменных имеет вид
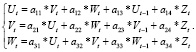(7)
Коэффициенты уравнений системы (1) и (4) связаны соотношениями
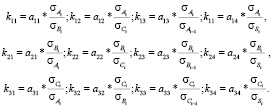(8)
Ниже представлена приведенная форма модели для системы со стандартизированными переменными (7)
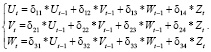(9)
Параметры δij определяются по материалам статических наблюдений обычным методом наименьших квадратов, процедура для реализации которого имеется в ряде пакетов прикладных программ, хорошо известных большинству пользователей.
Теперь осталось только установить связь между параметрами систем (7) и (9), т.е. найти преобразование, позволяющее выразить коэффициенты aij через коэффициенты δij. Для всех задач, решаемых в технике косвенного метода наименьших квадратов, этот момент является самым нетривиальным и требующим в каждом конкретном случае индивидуального подхода.
Найдем представление коэффициентов первого из уравнений системы (7) через коэффициенты приведенной формы системы (9). Исключим из первого уравнения системы (9) экзогенные переменные Vt-1 и Wt-1, которые не входят в первое уравнение структурной формы системы (9). С этой целью запишем второе и третье уравнения системы (9) в виде
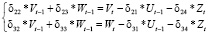(10)
и выразим отсюда переменные Vt-1 и Wt-1. После несложных преобразований получим
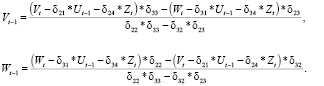(11)
Подставим полученные результаты в первое уравнение системы (9)
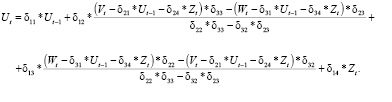(12)
Легко заметить, что уравнение (12) имеет в своем составе переменные Ut; Ut-1; Vt; Wt; Zt, т.е. именно те, что содержатся в первом стандартизированном уравнении структурной формы модели системы (7). Это позволяет получить выражение параметров данного уравнения через коэффициенты δij.
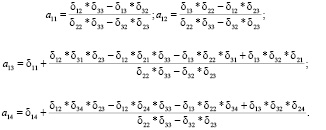(13)
Опустим технические подробности и запишем соотношения, выражающие параметры второго и третьего уравнений системы (7) через коэффициенты приведенной формы (9).
Коэффициенты второго уравнения:
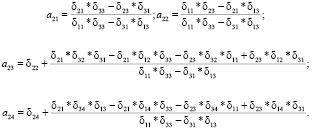(14)
Коэффициенты третьего уравнения:
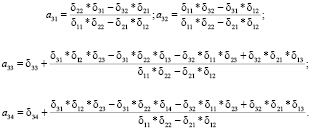(15)
После того как коэффициенты структурной формы модели определены для стандартизированных переменных, с помощью формулы (8) находят коэффициенты kij структурной формы модели (4) в натуральных переменных.
Вариантов использования данной модели может быть предложено несколько:
1. После прохождения входного контроля и выяснения начального уровня способностей A0; B0; C0, модель можно использовать для разработки карты учебного процесса, т.е. для отыскания степени сложности учебных проблем и распределения их по этапам так, чтобы по окончании обучения ABC-способности достигли уровня достаточного для освоения компетенций, предусмотренных стандартом образования. Эта карта может быть доведена до сведения обучаемого с тем, чтобы он мог взвесить свои возможности и рационально распределить силы.
2. Модель позволяет находить минимально допустимый уровень начальных способностей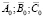 
при котором возможно достижение требуемого конечного результата. Эта позволит объективизировать процесс отбора обучаемых и сократить до минимума отсев непосредственно в ходе учебного процесса.
3. С помощью данной модели имеется возможность получить количественную оценку эффектов взаимовлияния различных способностей друг на друга, что, по мнению авторов, представляет большой научный интерес. Следует, однако, отметить, что для разных специальностей параметры модели, характеризующие эффекты влияния, могут быть существенно различны. Особенно ярко это должно проявляться для точных и прикладных наук и дисциплин гуманитарного направления.
Следует отметить, что проверка адекватности модели в целом и оценка значимости отдельных ее параметров выполнялась с использованием критериев Фишера и Стьюдента по известным статистическим методикам [4] и не содержит элементов новизны. Именно по этой причине авторы решили не приводить в тексте работы процедуру оценки адекватности.
Заключение
1. Выявлены интегративные параметры, которые положены в основу модели развития проектно-конструктивных способностей в псевдофазовом пространстве.
2. Предложен способ оценки вероятности успешного решения проблемы определенной сложности при известном деятельностном потенциале личности.
3. Разработана математическая модель развития деятельностного потенциала с использованием аппарата систем совместных регрессионных уравнений, которая может быть применена для построения целесо- образной траектории развития.
4. Разработанная модель является ядром для создания цифровых технологий в SMART online системах.
Библиографическая ссылка
Нуриев Н.К., Обади А.А., Печеный Е.А., Старыгина С.Д. МАТЕМАТИЧЕСКАЯ МОДЕЛЬ РАЗВИТИЯ ПРОЕКТНО-КОНСТРУКТИВНЫХ СПОСОБНОСТЕЙ В ДЕЯТЕЛЬНОСТИ // Современные наукоемкие технологии. – 2019. – № 7. – С. 70-77;URL: https://top-technologies.ru/ru/article/view?id=37592 (дата обращения: 21.11.2024).