Искусственные нейронные [1, 2] сети (ИНС) являются вычислительными структурами, состоящими из определенного количества однотипных элементов, соединённых между собой, названными искусственными нейронами. Каждый нейрон выполняет относительно простые функции, а именно получает и пересылает сигнал другим элементам данной сети. Часто данные процессы сравнивают с процессами, происходящими в нейронных сетях живых организмов, но искусственные нейронные сети имеют более простую структуру. В качестве примера для научных исследований был выбран многослойный персептрон [1, 2] (рис. 1).
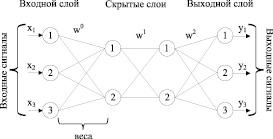
Рис. 1. Структура многослойного персептрона
Нейронные сети находят своё применение в различных сферах деятельности человека. В наше время нейронные сети используются для распознавания изображений [3, 4], получили применение в финансовой сфере [5]. Благодаря способности аппроксимировать нелинейность любого вида [1, 2] ИНС используют в различных отраслях промышленности. Например, ИНС используются в задачах идентификации и получения математических моделей газотурбинных установок (ГТУ) [6, 7], газотурбинных электростанций (ГТЭС) [8, 9]. Такие нейросетевые модели в дальнейшем используют в качестве объекта управления для настройки параметров регулятора системы автоматического управления (САУ). Кроме того, ИНС также используются в качестве системы диагностики газотурбинного двигателя [10].
Однако необходимо учесть, что чем сложнее поставлена задача перед исследователем, тем сложнее проходит процесс обучения нейронной сети. ИНС в основном разделяют на сети, которые обучаются с учителем, и те, которые обучаются без учителя [1, 2]. В данной статье будет рассматриваться метод обучения с учителем, использующий алгоритм обратного распространения ошибки [1, 2] для обучения полученной ИНС. Данный алгоритм является самым распространённым способом обучения нейронной сети, однако у данного метода есть ряд нюансов, как правило, этим алгоритмом обучают относительно не большие сети, с одним или несколькими скрытыми слоями, поскольку при увеличении структуры есть вероятность возникновения затухания, либо взрывного роста весов [11, 12]. Взрывной рост может произойти, если веса слишком большие, либо значение производной в точке слишком велико, а затухание происходит, если значение весов или производной в точке очень мало. Особенно такая ситуация характерна в случае реккурентных искусственных нейронных сетей, так как такие сети содержат обратные связи [1, 12].
Тонкая настройка ИНС
В ходе работы алгоритма обратного распространения ошибки происходит обновление весовых коэффициентов на каждой итерации обучения, начиная с выходного слоя по направлению к входному слою ИНС. В случае большого количества скрытых слоев наблюдается эффект затухания градиента [11, 12], то есть чем ближе к входному слою, тем меньше изменение весового коэффициента в ходе алгоритма обучения. Тем самым процесс обучения замедляется. Одним из способов решения возникшей проблемы является тонкая настройка весов (предобучение) нейронной сети [13, 14].
Предположим, для получения модели ГТЭС мы выбрали сеть прямого распространения следующей структуры: x1 → x2 → ... → xn. Каждый xi – это количество нейронов в слое, xn – выходной слой. Обозначим за x0 размерность входного вектора, который подается на вход слоя x1. Так же у нас есть массив данных для обучения D0 – это пары вида «вход, ожидаемый выход», и мы хотим обучить сеть, используя алгоритм обратного распространения ошибки. Но перед этим осуществим тонкую настройку весов каждого скрытого слоя по алгоритму, представленному на рис. 2.
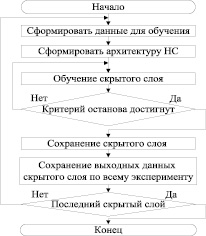
Рис. 2. Алгоритм тонкой настройки весов скрытого слоя
Визуализация данного алгоритма (рис. 2) представлена на рис. 3.
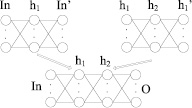
Рис. 3. Визуализация алгоритма тонкой настройки весов скрытого слоя
Где In – входной слой нейронной сети; h1 – первый скрытый слой нейронной сети; h2 – второй скрытый слой нейронной сети; О – выходной слой нейронной сети.
Для тестирования была взята архитектура нейронной сети без обратных связей, с двумя скрытыми слоями, по 10 нейронов в каждом скрытом слое.
Каждый из скрытых слоев ИНС был обучен по алгоритму (рис. 2), и из этих слоев была сформирована результирующая ИНС (рис. 3). В итоге были получены следующие результаты (рис. 4–5).
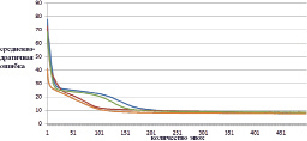
Рис. 4. Изменение ошибки по эпохам обучения для обучающей выборки (синяя, зеленая, красная – нет тонкой настройки; коричневая, голубая, фиолетовая – есть тонкая настройка)
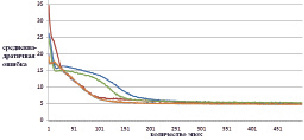
Рис. 5. Изменение ошибки по эпохам обучения для тестовой выборки (синяя, зеленая, красная – нет тонкой настройки; коричневая, голубая, фиолетовая – есть тонкая настройка)
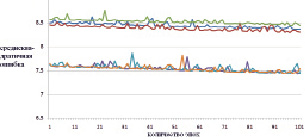
Рис. 6. Изменение ошибки последних 100 эпох обучения для обучающей выборки (синяя, зеленая, красная – нет тонкой настройки; коричневая, голубая, фиолетовая – есть тонкая настройка)
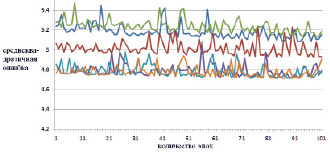
Рис. 7. Изменение ошибки последних 100 эпох обучения для тестовой выборки (синяя, зеленая, красная – нет тонкой настройки; коричневая, голубая, фиолетовая – есть тонкая настройка)
По рис. 4 и 5 наглядно видно, что в случае тонкой настройки весовых коэффициентов (предобучения) ИНС уменьшение ошибки происходит значительно интенсивнее. Рассмотрим последние 100 эпох обучения (рис. 6 и 7).
Заключение
Объяснение полученным результатам можно дать следующее: при обучении первого скрытого слоя ИНС создается модель, которая по экспериментальным данным, подаваемым на вход ИНС, генерирует некоторые скрытые признаки, то есть весовые коэффициенты ИНС сразу помещаются в некоторый минимум, необходимый для вычисления этих скрытых признаков. В дальнейшем, с каждым последующим обучением скрытых слоев ИНС, вычисляются признаки признаков, а весовые коэффициенты ИНС всегда помещаются в состояние, достаточное для вычисления этих иерархических признаков. Уже когда дело доходит до алгоритма обучения с учителем, по сути, эффективно обучаться будут только 2–3 слоя от выхода, на основании тех гиперпризнаков, что были вычислены раньше, а те, в свою очередь, будут незначительно меняться в угоду решаемой задачи.
Стоит отметить, что для проверки использовалась очень простая архитектура нейронной сети и небольшое количество экспериментальных данных, а также эпох обучения. В случае решения задачи с большим количеством экспериментальных и большого количества скрытых слоев ИНС, а также большего количества эпох обучения, разница между предварительно настроенной нейронной сетью и обычным способом инициализированной сетью должна оказаться значительнее.
Исследование выполнено при финансовой поддержке РФФИ и Пермского края в рамках научного проекта № 19-48-590012.
Библиографическая ссылка
Килин Г.А., Кавалеров Б.В., Шулаков Н.В., Ждановский Е.О. ТОНКАЯ НАСТРОЙКА НЕЙРОННОЙ СЕТИ В ЗАДАЧАХ ПОЛУЧЕНИЯ МАТЕМАТИЧЕСКОЙ МОДЕЛИ ГАЗОТУРБИННОЙ ЭЛЕКТРОСТАНЦИИ // Современные наукоемкие технологии. 2019. № 7. С. 41-44;URL: https://top-technologies.ru/ru/article/view?id=37587 (дата обращения: 31.12.2025).



