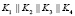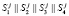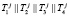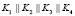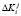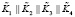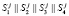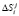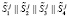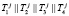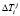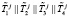Научный журнал

Современные наукоемкие технологии

ISSN 1812-7320

"Перечень" ВАК

ИФ РИНЦ = 0,940

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Калмыков И.А. 1 Степанова Е.П. 1 Чистоусов Н.К. 1 Калмыков М.И. 1 Тынчеров К.Т. 2

---

1 ФГАОУ ВО «Северо-Кавказский федеральный университет»

2 ФГБОУ ВО «Уфимский государственный нефтяной технический университет»

Перспективным направлением применения низкоорбитальных систем спутниковой связи являются автоматизированные системы дистанционного мониторинга, контроля и управления объектами добычи и транспортировки углеводородов Крайнего Севера. Для организации бесперебойной связи необходимо в состав группировки включить до 60 спутников. По мере увеличения числа стран, осваивающих месторождения Арктического шельфа, будет возрастать и количество группировок космических аппаратов. Это может привести к ситуации, когда спутник-нарушитель, оказавшись в зоне радиовидимости приемника, который располагается на абонентском терминале объекта, может навязать ранее перехваченную команду управления. В результате этого необслуживаемый объект добычи и транспортировки углеводородов может выйти из строя. Для предотвращения такой ситуации в статье предлагается использовать систему опознавания «свой-чужой». Для обеспечения высокой информационной скрытности в таких системах целесообразно использовать протокол аутентификации с нулевым разглашением знаний. С целью повышения скорости опознавания спутника предлагается использовать метод построения системы аутентификации КА низкоорбитальной системы спутниковой связи, использующий целочисленные алгебраические структуры конечных полей Галуа. Особое место среди последних занимают полиномиальные модулярные коды (ПМК), в которых арифметические операции выполняются независимо и параллельно по основаниям – неприводимым полиномам. Целью статьи является сокращение времени аутентификации спутника за счет использования ПМК.

Статья в формате PDF

0 KB

система аутентификации космического аппарата

модулярные коды

метод построения системы аутентификации

полиномиальные модулярные коды

1. Алёшин Б.С., Баженов С.Г., Диденко Ю.И. Системы дистанционного управления. М.: Изд-во «Наука», 2013. 292 с.

2. Rezenkov R.N., Pashintsev V.P., Zhuk P.A. Application of spoof resistant authentication protocol of spacecraft in low earth orbit systems of satellite communication. International Journal of Mechanical Engineering and Technology (IJMET). 2018. Vol. 9. Issue 5. Р. 958–965.

3. Smith R. Authenticaton: From Passwords to Public Keys. New York: Addison-Wesley Publishing Company, Inc., 2015. 352 р.

4. Запечников С.В. Криптографические протоколы и их применение в финансовой и коммерческой деятельности. М.: Горячая линия-Телеком, 2011. 256 с.

5. Пашинцев В.П., Ляхов А.В. Применение помехоустойчивого протокола аутентификации космического аппарата для низкоорбитальной системы спутниковой связи // Инфокоммуникационные технологии. 2015. № 2. С. 183–190.

6. Stepanova E.P., Toporkova E.V., Katkov R.A., Rezenkov D.N. Application of the codes of a polynomial residue number system, aimed at reducing the effects of failures in the AES cipher. Journal of Digital Information Management. 2016. № 14 (2). Р 114–123.

Известно, что низкоорбитальные системы спутниковой связи нашли широкое применение в таких глобальных проектах, как освоение Северного морского пути, создание информационно-телеметрических систем воздушного и наземного транспорта в высоких широтах. Особое место занимают проекты освоения шельфа Северного Ледовитого океана. В этом НССС входят в состав автоматизированных систем дистанционного мониторинга, контроля и управления (АСДМКУ) объектами добычи и транспортировки углеводородов [1]. Для организации связи состав группировки содержит от 48 до 60 спутников. Увеличение количества НССС может привести к ситуации, когда спутник-нарушитель попытается навязать перехваченную и задержанную команду управления, что приведет к отказу объекта управления.

Устранить такую ситуацию можно за счет повышения информационной скрытности НССС с помощью системы аутентификации спутника (САС) [2]. Чтобы повысить скорость аутентификации спутника, необходимо перейти к параллельным вычислениям, то есть использовать целочисленные алгебраические структуры полей Галуа – полиномиальные модулярные коды (ПМК). Применение данных кодов позволяет осуществить распараллелить вычисления на уровне арифметических операций. Поэтому разработка метода построения САС, базирующейся на ПМК, является актуальной задачей.

Материалы и методы исследования

Очевидно, что эффективность обеспечения информационной скрытности НССС определяется протоколом аутентификации, который используется в системе аутентификации спутника. Проведенный анализ работ [3, 4] показал, что множество протоколов аутентификации можно разбить на три группы. В первую группу входят протоколы парольной аутентификации. Однако данные протоколы аутентификации не могут использоваться для опознавания спутника, так как имеют низкую криптографическую стойкость. Основу второй группы составляют протоколы аутентификации типа «запрос – ответ». В этих протоколах, согласно [4], широко используются алгоритмы шифрования. Однако данные протоколы нельзя использовать в САС, так как необходимо хранить секретные ключи не только на спутниках и объектах.

Этого недостатка лишены протоколы аутентификации с нулевым разглашением знаний, которые образуют третью группу. Однако в таких протоколах необходимо выполнить от 40 раундов идентификации [4]. Снизить временные затраты позволяет протокол, который представлен в работе [5]. Он состоит из следующих этапов.

Для работы САС выбирают большое простое число М, а также секретный ключ K, параметры S и T, удовлетворяющие 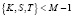. С помощью S и T вычисляются сеансовые ключи и параметр проверки повторного их использования

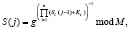
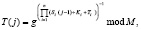(1)

где 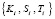– i-е блоки секретного ключа K, S и T; g – порождающий элемент; 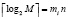; n – количество блоков размерностью mi разрядов каждый.

Первый этап. Перед началом j-го сеанса работы САС определяется истинный статус спутника, используя сеансовый ключ S(j) и параметры и параметр Т(j), согласно

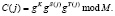(2)

Второй этап. Производится вычисление зашумленного статуса спутника, используя зашумленные значения K, S(j) и Т(j), согласно

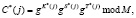(3)

где 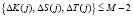– случайные числа зашумления; ; ; .

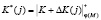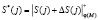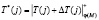Процедура аутентификации статуса спутника включает следующих два этапа.

Первый этап. Запросчик генерирует число 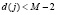, которое называется запросом, а затем передает его ответчику КА.

Второй этап. Ответчик отвечает на запрос d(j) согласно

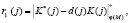
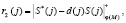
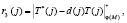(4)

где φ(M) – функция Эйлера простого числа М.

Затем ответчик пересылает запросчику сигнал в виде .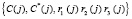

Процесс аутентификации спутника реализуется с помощью выражения

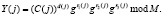(5)

Если результат совпал с С*(j), то спутник является «своим», и он может начать сеанс связи. В противном случае – спутник к каналу связи не допускается.

Согласно [4] для обеспечения высокой имитостойкости протокола аутентификации необходимо чтобы М имело не менее 128 разрядов, что приводит к значительным временным затратам на реализацию мультипликативных операций. Снизить время опознавания КА можно за счет использования целочисленных алгебраических структур полей Галуа, то есть ПМК.

В этих кодах в качестве оснований используются неприводимые полиномы pi(x), где i = 1, 2,..., k. Тогда целое число F переводится в полиномиальную форму F(x), которая заменяется набором остатков 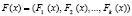, где 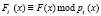[6]. Тогда для полиномиальных модулярных кодов справедливы выражения

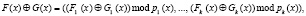(6)

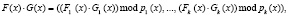(7)

где 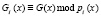; i = 1, 2,..., k.

Кортеж оснований ПМК задает величину рабочего диапазона

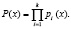(8)

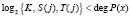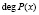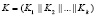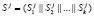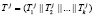Реализуем одномодульный протокол аутентификации спутника [5] с использованием целочисленных алгебраических структур полей Галуа. Выбираем параметры протокола, удовлетворяющие условию , где – степень полинома Р(х). Проводим конкатенацию выбранных параметров , и , где 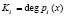, 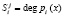; ; 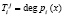i = 1, 2,..., k. Пусть порождающий элемент g = x.

Рассмотрим выполнение предварительных вычислений на j-ом сеансе проверки:

Первый этап. Ответчик, располагаемый на КА, определяет истинный статус

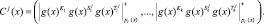(9)

Второй этап. Ответчик для вычисления зашумленного статуса КА выбирает случайные числа 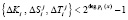и производит вычисление параметров

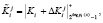
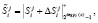
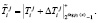(10)

Ответчик определяет зашумленный статус спутника, используя ПМК

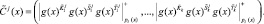(11)

Процедура аутентификации статуса спутника.

Первый этап. Запросчик передает спутнику в качестве запроса случайное число 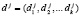, где 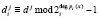; i = 1, 2,..., k.

Второй этап. Ответчик получает ответы на запрос 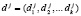, согласно

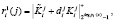
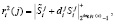
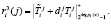(12)

Спутник передает запросчику следующие данные

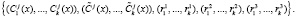
Процедура проверки ответов.

1. Запросчик проверяет ответы на вопрос .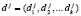

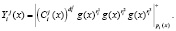(13)

Спутнику присвоят статус «свой», если справедливо

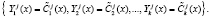(14)

Результаты исследования и их обсуждение

В качестве оснований 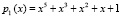, , 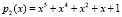, 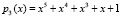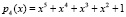. Значит, размер секретного ключа K, параметров S и T не должны превышать 20 разрядов. Пусть K = 836931, S = 467430 и T = 108667. В табл. 1 представлена их конкатенация.

Таблица 1

Двоичный код и конкатенация параметров протокола

1. Ответчик вычисляет истинный статус, представленный в ПМК, используя (9):

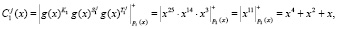
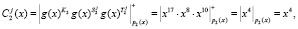
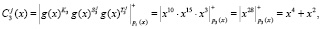
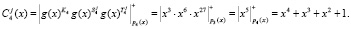
2. Ответчик для вычисления зашумленного статуса КА выбирает случайные числа 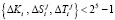. Результаты зашумления согласно (10) приведены в табл. 2.

Таблица 2

Зашумление параметров протокола

Согласно (11) ответчик определяет зашумленный статус спутника, используя ПМК

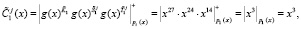
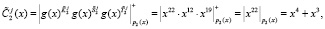
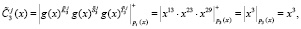
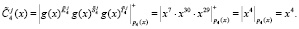
Рассмотрим процесс аутентификации статуса спутника.

1. Запросчик передает спутнику в качестве запроса случайное число .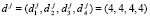

2. Ответчик вычисляет ответы на запрос, согласно выражения (12). Тогда ответы по первому модулю будут равны

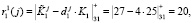
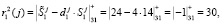
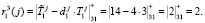
Ответы по второму модулю будут равны

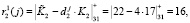
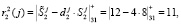
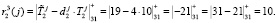
Ответы по третьему модулю будут равны

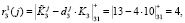
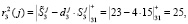
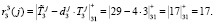
Ответы по четвертому модулю будут равны

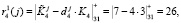
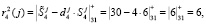
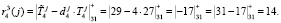
Спутник передает запросчику следующие данные:

– истинные статусы ;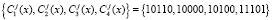

– зашумленные статусы ;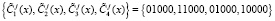

– первая группа ответов ;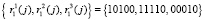

– вторая группа ответов ;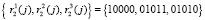

– третья группа ответов ;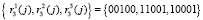

– четвертая группа ответов .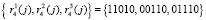

Рассмотрим процедуру проверки ответов согласно выражению (13). Получаем

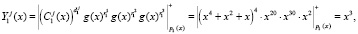
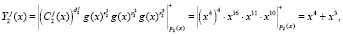
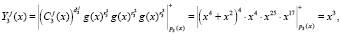
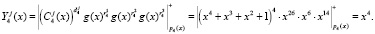
Полученные значения совпали с зашумленным статусом КА, представленным в ПМК. Значит, статус аутентифицируется как «свой», и ему предоставляется сеанс связи.

В рассмотренном примере использование разработанного метода построения САС на основе ПМК позволило повысить скорость аутентификации спутника. Известно, что время выполнения мультипликативных операций пропорционально разряду операндов. При использовании одномодульного протокола аутентификации разрядность данных составляла 20 разрядов. При переходе к ПМК разрядность операндов сократилась до 5 бит. Значит, за счет распараллеливания вычислений на уровне операций в ПМК скорость аутентификации КА повысилась в 4 раза по сравнению с протоколом [5].

Выводы

В статье представлен разработанный метод построения системы аутентификации спутника для НССС на основе полиномиальных модулярных кодов. Распараллеливание вычислений на уровне операций, которое обеспечивают ПМК, повысит скорость аутентификации спутника. В приведенном в статье примере был использован протокол аутентификации, в котором разрядность данных составляла 20 разрядов. При переходе к ПМК разрядность операндов сократилась до 5 бит. Значит, за счет распараллеливания вычислений на уровне операций в ПМК скорость аутентификации КА повысилась в 4 раза по сравнению с протоколом [4].

Исследование выполнено при финансовой поддержке РФФИ в рамках научного проекта № 18-07-01020.

Библиографическая ссылка