Стационарные паровые турбины типа «ПТ», как правило, имеют два регулируемых отбора пара: производственный и теплофикационный. Для штатного подключения и отключения линий отборов на паропроводы устанавливаются электроприводные задвижки, скорость перемещения которых ограничена и составляет обычно несколько десятков секунд. Однако во время работы турбины возможно возникновение ряда аварийных ситуаций, при которой вместе с остановом самой турбины требуется быстро закрыть и её отборы для предотвращения обратного потока пара в турбину из коллектора питаемой тепловой сети. Для решений этой задачи в составе паровых турбин ОАО «КТЗ» [1] зачастую используются обратные клапаны поворотного типа c условными диаметрами Dy от 150 до 500 мм. Такой клапан представляет собой поворотную заслонку, подвешенную в трубопроводе отбора на горизонтальной оси. В нерабочем состоянии захлопка закрыта и плотно прижата к своему седлу пружиной в составе привода. При необходимости подачи пара в отбор на привод заслонки подаётся команда на взвод, в результате которой действие пружины преодолевается гидравликой и заслонка становится разгруженной, благодаря чему и открывается потоком пара (для начала открытия, как правило, достаточно перепада давления всего ~15 кПа). При возникновении обратного потока пара этот же перепад давления и закрывает заслонку, действуя вместе с собственной силой тяжести заслонки. Таким образом, реализована быстродействующая защита. Проблемой при этом является то, что под воздействием больших перепадов давления в паропроводе с разных сторон захлопки происходит слишком быстрое ее закрытие, и в совокупности с большими габаритами и массой этой захлопки возникает сильный удар о седло, что ведет к его разрушению и заклиниванию самой захлопки в седле. Во избежание подобных дефектов применяются ряд конструктивных приспособлений [1, 2], таких как:
– ограничительные упоры;
– демпфер пружинного типа;
– демпфер гидравлического типа.
Целью настоящей работы является исследование и выработка рекомендаций по конструкции и настройке последнего типа, как наиболее функционального и эффективного. Такой демпфер способен с переменной скоростью замедлять закрытие захлопки при подходе к седлу и тем самым уменьшать силу удара о него. Одним из возможных путей решения данной проблемы является проведение динамических исследований демпфера при различных условиях работы захлопки, некоторые результаты по которым имеются [3, 4]. Однако целесообразным представляется и динамическое исследование с использованием адекватной математической модели объекта, что значительно упрощает сам процесс исследования, сокращает временные и материальные затраты на проведение самих исследований и снимает риски аварийных ситуаций. Для проведения такого исследования необходима разработка математической модели реальной захлопки Dy400 Py80 (рис. 1) с гидравлическим демпфером, представленная ниже в первой части работы.
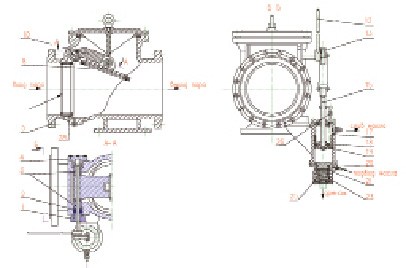
Рис. 1. Конструкция обратного клапана-захлопки Dy400 Pу80 с гидравлическим демпфером, Основные детали: 1 – фланец нажимной, 2 – сальник, 3 – втулка, 4 – крышка, 5 – корпус, 8 – клапан, 10 – рычаг клапана, 12 – рычаг, 13 – рычаг привода клапана, 15 – шток привода, 17 – цилиндр, 18 – пружина, 19 – поршень, 20 – седло ускорителя, 21 – поршень ускорителя, 23 – пружина ускорителя, 25 – корпус ускорителя, 26 – установка концевых выключателей, 28 – седло
Построение адекватной математической модели является сложной и трудоёмкой задачей, поскольку энергетические объекты, в частности турбины, относятся к классу существенно нелинейных объектов, и при построении модели достаточно трудно учесть все внешние и внутренние факторы, влияющие на работу рассматриваемого объекта [5]. Даже если и удаётся построить модель, учитывающую наиболее важные факторы, остается проблема с определением числовых значений параметров модели, поскольку большинство параметров имеет справочные значения, определенные при стандартных условиях, что существенно отличается от условий эксплуатации [6]. Для решения данной проблемы можно воспользоваться методами параметрической идентификации, которые позволяют уточнить числовые значения по результатам натурных испытаний [7].
Ниже рассматривается решение задачи построения математической модели клапана-захлопки в режиме форсированного закрытия на основе методов исследования динамики и моделей гидро- и пневмоприводов [8].
На рис. 1 представлена конструкция обратного клапана-захлопки Ду 400, а на рис. 2 представлены экспериментальные данные по скорости ее закрытия в зависимости от перепада давления пара на ней.
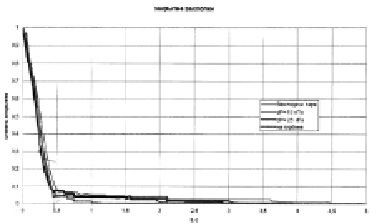
Рис. 2. Экспериментальный график зависимости степени закрытия захлопки от времени при различных перепадах давления пара
Конструктивные особенности захлопки с приводом и экспериментальные данные по скорости её закрытия могут быть положены в основу её математической модели.
Построение математической модели
При построении математической модели будем учитывать наличие гидравлического демпфера, который вступает в работу на конечном этапе закрытия клапана-захлопки. Кроме того, необходимо учитывать процесс истечения рабочей жидкости из нижней полости гидравлического цилиндра в дренажную линию [8], что также может усложнить модель рассматриваемого объекта. Однако, исходя из полученных экспериментальных данных, процесс закрытия протекает достаточно медленно и, следовательно, динамикой изменения давления в демпфере и в нижней полости гидроцилиндра можно пренебречь. Также будем пренебрегать аэродинамическими процессами обтекания паром захлопки ввиду их квазистационарного характера при малых углах открытия. Следовательно, для построения динамической модели клапана в первом приближении достаточно рассмотреть баланс сил, действующих на поршень гидравлического цилиндра привода.
Из конструкции захлопки следует, что в качестве сил, под действием которых будет закрываться клапан, будут выступать: сила тяжести, сила со стороны деформированной возвратной пружины, а также момент сил, действующих на захлопку – сумма момента силы тяжести и момента, вызванного перепадом давления пара.
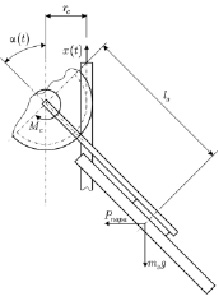
Рис. 3. Схема определения нагрузки со стороны захлопки
В качестве «отрицательных сил» будут выступать: инерционные силы подвижных частей гидроцилиндра; инерционный момент захлопки; силы и моменты сухого и вязкого трения гидроцилиндра и захлопки.
С учётом этого и расчётной схемы, представленной на рис. 3, можно записать следующее уравнение:
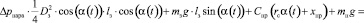
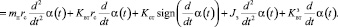
Здесь α(t) – текущий угол открытия захлопки (причём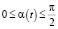 
); Δpпара – перепад давления пара на захлопке; Dз – диаметр захлопки; lз – расстояние от центра клапана до оси вращения; mз – его масса; g – ускорение свободного падения; Cпр – жесткость возвратной пружины; хпр – начальное поджатие возвратной пружины; rс – радиус сектора реечной передачи; mп – масса подвижных частей гидроцилиндра; Kвт и Kст – соответственно коэффициенты вязкого и сухого трения подвижных частей гидроцилиндра; Jз – момент инерции заслонки относительно оси вращения; Kзвт – момент коэффициента вязкого трения в оси заслонки.
Поскольку динамикой процессов, протекающих в демпфере и при истечении жидкости из нижней полости гидроцилиндра, пренебрегаем, то демпфер можно рассматривать как дополнительное сопротивление, и, следовательно, коэффициент Kвт можно рассматривать как «составной», учитывающий вязкое трение, сопротивление истечение жидкости из отверстия и демпфер, который «включается» на конечном участке закрытия клапана; т.е. Kвт = Kзвт и можно определить как: Kзвт = Kвт, если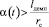 
, и 
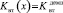, если 
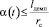, где lдемп – длина хода демпфера, и 
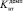значительно больше Kвт.
Пренебрегая сухим трением, окончательно получим
,
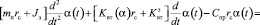
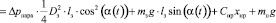или
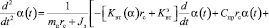
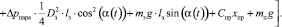(1)
Последнему уравнению будет соответствовать структурная схема, представленная на рис. 4.
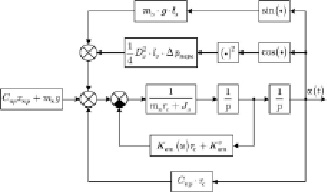
Рис. 4. Структурная схема математической модели захлопки
Кроме того, на значение угла накладываются ограничения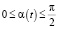 
и начальными условиями для решения последнего уравнения являются 
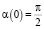и 
.
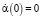Параметрическая идентификация
В полученной математической модели клапана-захлопки большинство параметров являются конструктивными, значения которых определяются геометрией и характеристиками материала, из которых они изготовлены. Уточнению подлежит параметр Kвт = Kвт(α), поскольку в соответствии с допущениями данный параметр включает коэффициент вязкого трения, зависящего от условий эксплуатации и характеристик используемой рабочей жидкости, и учитывает сопротивление, возникающее при истечении рабочей жидкости из рабочей полости гидроцилиндра в дренажную линию и сопротивление со стороны демпфера. Поэтому числовое значение данного параметра необходимо уточнить по результатам эксперимента.
В качестве критерия совпадения угла открытия захлопки, полученного при решении дифференциального уравнения модели, с экспериментальными данными, воспользуемся критерием [3, 7]
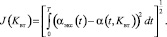(2)
Здесь αэкс(t) – экспериментально полученная зависимость угла открытия захлопки от времени; α(t, Kвт) – решение уравнения (1) модели захлопки; T – интервал исследования.
Задача уточнения числового значения коэффициента Kвт решается в два этапа. На первом этапе подбирается значение, соответствующее участку траектории, на котором не задействован демпфер. Минимизируя функционал (2) при начальных условиях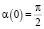 
и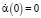 
решения уравнения (1), находим значение коэффициента Kвт, которое будет учитывать коэффициент вязкого трения и сопротивление истечению жидкости из полости гидроцилиндра в дренажную линию. В результате решения для данного участка получено следующее оптимальное значение: K*вт = 13605. На этом же этапе определяется скорость закрытия захлопки и значение угла на момент времени, соответствующий началу демпфирования, которые будут являться начальными значениями для нахождения решения уравнения (1) при минимизации функционала (2) на втором участке. Для данного участка K*вт = 2102062. Таким образом,
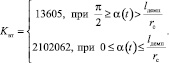(3)
На рис. 5 представлены результаты моделирования для (3) при различных перепадах давления пара на захлопке, из которых видно, что построенная математическая модель для сделанных допущениях с приемлемой точностью описывает протекающие процессы при закрытии клапана-захлопки.
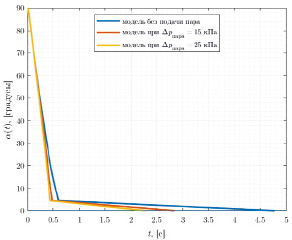
Рис. 5. Графики изменения угла открытия захлопки от времени
Заключение
Построенная математическая модель с учётом сделанных допущений является упрощенной и поэтому может быть использована для предварительной оценки времени закрытия клапана-захлопки, и тем самым можно оценить соответствие рассматриваемого объекта предъявляемым в техническом задании требованиям. В дальнейшем планируется повысить адекватность построенной модели путем учёта дополнительных факторов, в частности моделей демпфера и истечения жидкости из полости гидроцилиндра в дренажную линию, с последующим уточнением числовых значений параметров модели по экспериментальным данным. Конечной целью является исследование влияния и оптимизация размеров отверстия и поршня демпфера с точки зрения обеспечения наискорейшего и безударного закрытия (посадки на седло). Оно будет проведено на последующих этапах работы.
Библиографическая ссылка
Чубаров Ф.Л., Акименко Д.А., Сизов А.Н., Никитин А.В. РАЗРАБОТКА МАТЕМАТИЧЕСКОЙ МОДЕЛИ КЛАПАНА-ЗАХЛОПКИ ДЛЯ ОПТИМИЗАЦИИ ЕГО ДЕМПФИРОВАНИЯ ПРИ ЗАКРЫТИИ // Современные наукоемкие технологии. – 2019. – № 6. – С. 119-125;URL: https://top-technologies.ru/ru/article/view?id=37560 (дата обращения: 21.11.2024).