Подвеска является одним из наиболее ответственных узлов автомобиля, определяющим совокупность эксплуатационных свойств – плавность движения, устойчивость и управляемость, среднюю и максимальную скорость, долговечность ряда деталей и узлов. Вместе с шинами подвеска является основным конструктивным элементом, защищающим автомобиль от динамических воздействий со стороны дороги до уровня, приемлемого в соответствии с требованиями нормативных документов и прочности элементов конструкции. Правильно спроектированная подвеска позволяет снизить расходы на техническое обслуживание и ремонт, расширить эксплуатационные возможности автомобиля.
Вопросы проектирования подвесок автомобилей изучены достаточно подробно, однако выбор оптимального конструктивного варианта с учетом многочисленных факторов, влияющих не только на отдельных показатели, но и и в целом на эксплуатационные свойства автомобиля, во многих случаях затруднителен.
Особенностью практических методов проектирования является их узкая направленность, позволяющая решать отдельные задачи без учета последствий принятых решений на достаточно широкий спектр эксплуатационных свойств автомобиля. Для принятия эффективных конструкторских решений необходима разработка методики проектирования подвески, которая будет обеспечивать возможность многокритериальной оптимизации параметров и характеристик её функциональных элементов и обеспечивать очевидность принятых решений в отношении их влияния на основные эксплуатационные свойства автомобиля, определяющие безопасность и потребительскую привлекательность автомобиля.
Материалы и методы исследования
На эксплуатационные свойства автомобиля существенно влияют следующие параметры и характеристики подвески.
Жесткость подвески с механическим упругим элементом для многих конструктивных вариантов остается постоянной или меняется дискретно при изменении нагрузки, практически мало влияя на показатели плавности движения.
Демпфирующие свойства амортизатора существенно влияют на показатели плавности движения автомобиля. Обеспечивая гашение относительных колебаний подрессоренных и неподрессоренных масс автомобиля, амортизатор, жестко связанный с несущей системой и неподрессоренной частью автомобиля, способствует передаче дополнительного усилия на кузов.
При проектировании подвески целесообразно оценить возможные интервалы изменения k и степень влияния на величину оптимального значения kо параметров: приведенной жесткости подвески – Cп, скорости движения автомобиля – Vа, массы автомобиля – M и средних квадратичных значений неровностей микропрофиля – σq.
Относительные перемещения неподрессоренных масс опосредовано влияют на траекторную и курсовую устойчивость автомобиля. Учитывая, что величина нормальной реакции на колесо определяет силу трения (сцепления) колеса с дорогой и зависит от деформации упругого элемента и относительной скорости перемещения подрессоренной и неподрессоренной масс, целесообразно оценить влияние на характер контакта колеса с дорогой характеристик упругих элементов и амортизаторов.
Кинематические характеристики подвески полностью определяются конструктивными особенностями направляющих устройств подвесок. При моделировании динамики автомобиля должно быть учтено влияние деформации упругого элемента подвески на углы установки колес и на колею колес. Динамический анализ кинематических характеристик подвески при моделировании в реальных дорожных условиях позволяет учесть дополнительные факторы и нагрузки, которые могут влиять на показатели устойчивости курсового движения и управляемость автомобиля при экстремальных режимах, например связанных с экстренным торможением или резким поворотом.
Устойчивость подвески как динамической системы может существенно влиять на курсовую устойчивость автомобиля. При неудачном сочетании параметров (масс, размеров, жесткости, демпфирования, моментов инерции) динамической системы, состоящей из подвески в совокупности с поворотным узлом и колесом, в определенных интервалах скоростей движения, в результате управляющего воздействия на колеса возможны их колебания относительно оси поворота, называемые автоколебаниями.
В общем случае, для формирования возмущения от дорожной поверхности необходимо учитывать, что возмущение (входной сигнал) определяется распределением ординат микропрофиля по правой qп(t) и левой qл(t) колеям поверхности движения, а расчетная модель автомобиля должна иметь количество входов, соответствующих количеству колес (или пар колес). Для решения широкого круга задач динамики автомобиля могут быть использованы пространственные модели разной степени сложности, например математическая модель, расчетная схема которой представлена на рис. 1. Пространственная модель автомобиля состоит из пяти твердых тел: несущей системы (подрессоренная масса, кузов) и четырех колес (неподрессоренная масса). Кузов соединен с колесами вязко-упругими опорами, обладающими линейными или нелинейными характеристиками. Колеса (шины) автомобиля обладают вязко-упругими свойствами, неподрессоренные массы передней и задней подвесок отнесены к соответствующим колесам. Подобные модели используются для исследования динамики движения колесных машин по опорным поверхностям в прямолинейном или криволинейном движениях [1].
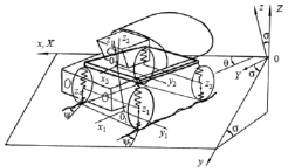
Рис. 1. Пространственная математическая модель колесной машины
При исследовании динамики подвески в качестве считаем, что действующие возмущения в основном формируются характером случайного распределения высот неровностей «q» микропрофиля поверхности дороги. Свойства микропрофиля дороги исчерпывающе описываются известными статистическими параметрами и характеристиками – средним значением ординат mср, средним квадратическим отклонением qq или дисперсией ординат Dq и спектральной плотностью дисперсий Sq(θ).
Исчерпывающей характеристикой любого случайного процесса является спектральная плотность дисперсий. Общепринятыми методами представления неровностей микропрофиля дорожной поверхности как у нас в стране, так и за рубежом являются аппроксимации спектральной плотности дисперсий, характеризующие плотность распределения дисперсии процесса по частотам, содержащую одновременно информацию о частотном и амплитудном составе случайного процесса [2].
В микропрофиле дороги содержатся неровности различной длины, которые могут вызывать возмущения разной частоты. Указанные параметры связаны соотношениями
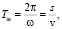 (1)
(1)
где Tω – время проезда неровности, с; ω – частота воздействия дорожных неровностей, рад/с; v – скорость автомобиля, м/с; s – длина неровности, м.
В практике расчетов целесообразно выбирать интервал длин неровностей (ограничивать максимальную длину неровности) в зависимости от установленного частотного диапазона исследуемого процесса и скорости движения автомобиля. Наиболее длинными неровностями smax можно считать такие, при проезде которых частота воздействия ωsmax примерно равна
ωsmax = 0,5ω0, (2)
где ω0 – собственная минимальная частота колебаний подрессоренной массы.
С учетом выражения (1) циклическая частота колебаний равна
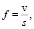 (3)
(3)
где f – циклическая частота, ω = 2πf [с-1].
Например, при собственной минимальной частоте подвески f0 = 1 Гц, проезд наиболее длинной неровности smax должен вызывать возмущение частотой не менее 0,5 Гц. При этом для скорости движения равной 100 км/ч (27,8 м/с) и минимальной длине неровностей 0,4 м, максимальная длина неровности, учитываемой при исследовании динамической системы, должна быть не менее s = 27,8/0,5 = 55,6 м, а верхняя граница частотного диапазона возмущений не менее fmax = 27,8/0,4 = 69,5 Гц (при исследовании с помощью третьоктавных фильтров 63,5 или 80 Гц).
При аналитических исследованиях динамических систем используют понятия частота по времени и частоте дороги (путевая частота), связанные зависимостями
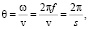 (4)
(4)
где θ – путевая частота [м-1].
С учетом выражения (4) циклическая частота процесса равна
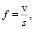 (5)
(5)
где f – циклическая частота ω = 2πf [с-1].
При расчетах приходится переходить от случайной функции q(x) к случайному процессу q(t) и от спектральной плотности дисперсии путевой частоты Sq(θ) к спектральной плотности частоты воздействия Sq(θ), связанных зависимостью
S(θ) = v Sq (ω). (6)
Таким образом, для перехода от зависимости Sq(θ)к Sq(ω) необходимо изменить масштабы по осям абсцисс и ординат так, чтобы выполнялось соотношение
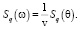 (7)
(7)
Такая замена не влияет на величину дисперсии, определяемую выражением
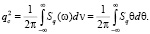 (8)
(8)
Ординаты микропрофиля находятся в относительно узком интервале значений, определяемом функцией распределения.
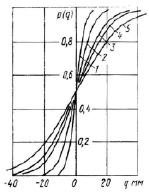
Рис. 2. Функции распределения ординат микропрофиля дорог: 1, 2 – цементобетонных, 3 – асфальтобетонной, 4 – грунтовой, 5 – булыжной
На рис. 2 показаны функции распределения ординат микропрофиля некоторых дорожных поверхностей [3]. Между высотой неровности и её длиной существует статистическая взаимосвязь. Средние квадратические значения ординат микропрофиля для цементно- и афальтово-бетонных покрытий удовлетворительного качества составляют 0,45–1,4 см2, для булыжных покрытий в зависимости от вида 2,5–3,3 см2. Функции распределения ординат микропрофиля поверхностей автомобильных дорог позволяют сделать вывод о том, что с вероятностью 90 % среднее квадратическое значение ординат микропрофиля не превышает 12 мм для цементобетонных дорог и 18 мм для асфальтовых, а ординаты микропрофиля находятся в достаточно узких интервалах значений. Вид функций распределения соответствует нормальному закону, в результате может быть использовано известное правило определения практически возможного значения ординаты микропрофиля (вероятность превышения которого составляет не более 0,3 %).
qmax ≈ 3qc. (9)
При расчетах колебаний автомобиля необходимо моделировать возмущение, создаваемое микропрофилем дороги. Основными способами математического описания параметров микропрофиля дороги являются:
– аналитическое выражение функции единичных неровностей и отдельных гармонических составляющих макропрофиля;
– задание экспериментально определенных ординат неровностей в зависимости от длины пути в виде массива данных;
– генерирование случайного микропрофиля поверхности дороги по статистическим характеристикам.
В настоящее время разработан ряд методов моделирования стационарных случайных процессов с заданными статистическими характеристиками: математическим ожиданием, дисперсией, корреляционной функцией или спектральной плотностью. Методы основаны на построении соответствующего вычислительного алгоритма, обеспечивающего получение реализаций случайных процессов. Методы могут быть классифицированы по степени точности [4]:
– точные методы (метод рекуррентных алгоритмов, дискретизации);
– приближенные (метод формирующего фильтра, скользящего суммирования).
Простейшие способы моделирования возмущения дороги основаны на детерминистических представлениях и реализуются с использованием аналитических зависимостей. Считается, что шина сглаживает очертания неровностей, что позволяет принять допущение о синусоидальной форме профиля неровности, симметричном относительно её среднего значения. Такой способ моделирования возмущения целесообразно использовать для исследования динамики автомобиля с помощью простых математических моделей, обеспечивающих удовлетворительную оценку динамических характеристик в переходном и установившемся режимах на начальных этапах проектной работы. Способ может быть использован и для формирования непрерывного гармонического возмущения.
Моделирование случайного возмущения дороги в виде числовой последовательности предполагает, что в общем случае микропрофиль дороги представляет случайную функцию, подчиняющуюся распределению Гаусса. Генерирование микропрофиля дороги [5] ставит целью получение реализации случайного процесса в виде числовой последовательности ординат функции, удовлетворяющей свойствам стационарности, эргодичности, распределенных по нормальному закону и имеющую корреляционную функцию экспоненциально-косинусного вида.
Алгоритм получения ординат микропрофиля дороги состоит из операций: формирование псевдослучайной равномерно распределенной числовой последовательности, формирование из равномерной числовой последовательности нормально распределенной, получение псевдослучайной числовой последовательности с заданными особенностями спектра из нормально распределенной числовой последовательности. Для получения псевдослучайной числовой последовательности с равномерным распределением в заданном интервале используется стандартный генератор или рекуррентная процедура.
Полученная таким способом случайная величина будет иметь равное нулю математическое ожидание и дисперсию, равную σ2. Для получения нормально-распределённой числовой последовательности ξ[n] с корреляционной функцией заданного типа используют моделирующий алгоритм, зависящий от вида корреляционной функции, реализуемый в соответствии с определенным алгоритмом. Моделирование случайного возмущения микропрофиля дороги рядом Фурье основано на предположении, что случайная функция q(s), имеющая ограниченную вариацию и непрерывная, может быть представлена в виде суммы тригонометрического ряда Фурье, состоящего из бесконечного множества гармонических составляющих функций. Ряд, состоящий из синусоидальных и косинусоидальных составляющих функций с амплитудами θ1n и θ2n дает наименьшую ошибку и является наилучшим приближением к функции q(s). С увеличением числа суммируемых членов ряда «n» точность представления функции увеличивается. Ряды Фурье позволяют использовать амплитудные спектральные диаграммы для определения дисперсии Dq. Использование рядов Фурье целесообразно для аналитического представления обособленных и групповых неровностей произвольной формы. Моделирование случайного возмущения в виде интеграла на практике возможно только при определенных допущениях в отношении количества гармонических составляющих случайного процесса, которое не может быть бесконечным. Генерирование случайного возмущения микропрофиля дороги методом формирующего фильтра основано на возможности формирования функции микропрофиля как случайного процесса по спектральной плотности его дисперсий. Наиболее значимым нормативным документом, классифицирующим дорожные поверхности, можно считать ISO 8608 [5]. Аппроксимации спектральной плотности дорожного воздействия зависят от угловой частоты процесса Ψ(ω). Для получения дискретных значений высоты микропрофиля в зависимости от времени при установленном шаге дискретизации, необходимо построить формирующий фильтр – динамическую систему, преобразующую случайный процесс ω(t) вида «белого шума» в случайный процесс zR(t) с заданными статистическими характеристиками. Вид (форма) передаточной функции формирующего фильтра определяется в соответствии с аппроксимацией спектральной плотности профиля дорожного полотна.
Результаты исследования и их обсуждение
Реализация вышеуказанной задачи выполняется методом блочного имитационного моделирования в программном комплексе MATLAB/Simulink. На рис. 3 приведена блок-схема разработанной модели. Блок Band-Limited White Noise (генератор белого шума) служит для создания шумового сигнала с заданной мощностью, равномерно распределенной по частоте. Генератор характеризуется мощностью шума Noise Power, эталонным временем Sample time и числом Seed, служащим для инициализации генератора случайных чисел. Генератор фактически является квантователем непрерывного сигнала, представляющего белый шум.
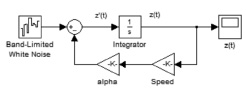
Рис. 3. Блок-схема Simulink-модели
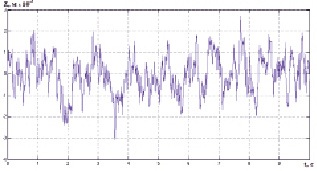
Рис. 4. Случайный процесс воздействия микропрофиля, V=60 км/ч, тип дороги – изношенность средняя
На рис. 4 представлен пример графической интерпретации результатов моделирования возмущения микропрофиля.
Авторами предложен метод генерирования случайного возмущения микропрофиля дороги по его спектральной плотности методом суммирования гармонических составляющих, базирующийся на известных представлениях о возможности представления случайного процесса с заданными характеристиками суммой гармонических составляющих. Подобная форма представления случайного возмущения микропрофиля дороги используется в некоторых работах по исследованию динамики подвески [6]. При решении практической задачи формирования непрерывного случайного возмущения в виде суммы гармонических составляющих в настоящей работе предлагается учитывать корреляцию амплитуд волн дорожных неровностей с их длинами, выявляемую с помощью характеристики спектральной плотности дисперсии микропрофиля. При моделировании возмущения используют спектральные характеристики микропрофиля, полученные любым из известных методов [2–6]. Частоты гармонических составляющих случайного процесса возмущения могут выбираться на линейной шкале с заданной степенью дискретизации или соответствующими центральным частотам октавных или третьоктавных диапазонов. Амплитуда гармонической составляющей определяется в соответствии со значением дисперсии для заданного частотного диапазона спектральной характеристики.
Дисперсия ординат микропрофиля в пределах выделенного частотного диапазона вычисляется в зависимости от формы представления (метода определения) спектральной плотности по соответствующим формулам. Частота гармонического возмущения может приниматься равной начальной или средней частоте выделенного диапазона, амплитуда синусоидальной волны неровности рассчитывается в соответствии с выражением
q0 = 1,43qс. (10)
На рис. 5 показана схема формирования возмущения от микропрофиля дорожной поверхности с использованием метода суммирования гармонических составляющих процесса. График характеристики дисперсии ординат микропрофиля как функции длины волны (неровности) разбивается на составляющие с кратными интервалами путевой частоты или длины волны.
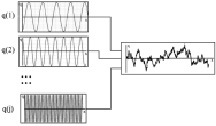
Рис. 5. Схема моделирования возмущения микропрофиля дороги
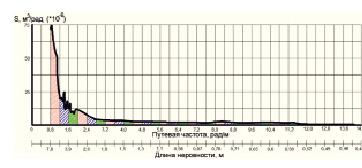
Рис. 6. Спектральная плотность булыжной дороги ровного замощения
На рис. 6 показана спектральная плотность булыжной дороги ровного замощения полигона «Березовая пойма». Частота каждого из выделенных интервалов соответствует частоте одной из гармонических составляющих. Текущие значения ординат гармонической составляющей возмущения могут задаваться с помощью аналитического выражения функции микропрофиля характерной синусоидальной формы.
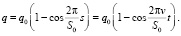 (11)
(11)
Для вывода выражений коэффициента демпфирования и динамической жесткости шины необходимо составить дифференциальное уравнение затухающих колебаний масс системы. В рассматриваемой колебательной системе энергия колебаний масс расходуется на работу против сил сопротивления и сил внутреннего трения в шине.
Считаем, что сила сопротивления, действующая при колебаниях, пропорциональна скорости
Fc = –rv, (12)
где r – коэффициент сопротивления; v – вектор скорости.
На рис. 7 показана модель микропрофиля булыжной дороги ровного замощения, реализованная в соответствии с описанным методом. Сравнение результатов моделирования и реальных замеров показало правомерность применения данного метода [8].
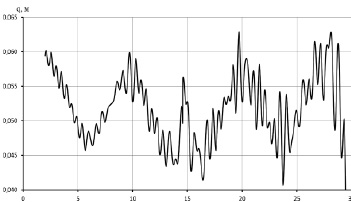
Рис. 7. Модель микропрофиля булыжной дороги ровного замощения
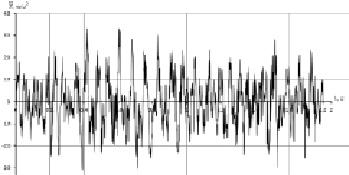
Рис. 8. Вертикальные ускорения на лонжероне, ровный булыжник, скорость 30 км/ч
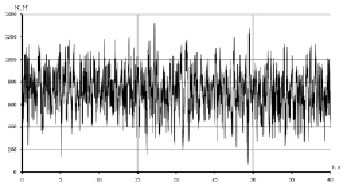
Рис. 9. Нормальная реакция на переднем колесе, ровный булыжник, скорость 30 км/ч
В результате расчетов с использованием модели автомобиля (рис. 1) и модели неровностей микропрофиля булыжной дороги ровного замощения получены случайные процессы вертикальных ускорений на лонжероне автомобиля над осью передних колес (рис. 8) и нормальной реакции на переднем колесе (рис. 9) [9].
Заключение
В результате проделанной работы можно сделать вывод о высокой эффективности использования компьютерного моделирования при анализе динамики подвески. Однако особое внимание следует уделить формированию возмущения от дорожной поверхности. Предложенный в данной статье способ отличается от остальных тем, что в его основе лежит реальная спектральная характеристика дороги (булыжник ровного мощения). Основной задачей для дальнейшего исследования является получение данных характеристик для других типов дорог.
Исследования выполнены при финансовой поддержке Министерства науки и высшего образования России в рамках проекта «Создание высокотехнологичного производства безопасных экспортоориентированных автомобилей ГАЗ с элементами автономного управления и возможностью интеграции с электроплатформой на базовых компонентах российского производства» по договору № 03.G25.31.0270 от 29.05.2017 г. (постановление Правительства Российской Федерации от 09 апреля 2010 г. № 218).
Библиографическая ссылка
Малеев С.И., Огороднов С.М., Степанов Е.В., Пинчин А.В. АНАЛИТИЧЕСКИЕ ИССЛЕДОВАНИЯ ДИНАМИКИ ПОДВЕСКИ // Современные наукоемкие технологии. 2019. № 6. С. 88-95;URL: https://top-technologies.ru/ru/article/view?id=37555 (дата обращения: 13.03.2026).
DOI: https://doi.org/10.17513/snt.37555



