Человеко-машинные системы находят все более широкое применение в различных отраслях промышленности и производства, при этом значительные средства вкладываются в разработку технологий коллективной робототехники и в решения связанных с ними специфичных проблем, одной из которых является распределение задач между автоматизированными процессами на различных уровнях систем управления и планирования [1], методики решения которой схожи с решениями сложных комбинаторных проблем [2]. Анализ публикаций показал, что для подобных задач часто используются искусственные нейронные сети [3–5], методы перебора [6], графовые методы [7], методы математического и динамического программирования [8].
Широкое использование вышеперечисленных подходов при распределении задач в процессах с высокой динамикой (характерно для коллективной робототехники) ограничивается их вычислительной сложностью, а эффективная реализация – ресурсами и быстродействием бортовых устройств мобильных роботов (требование миниатюризации габаритов и снижение энергопотребления роботов – агентов коллектива, что не позволяет размещать на мобильной платформе высокопроизводительные вычислительные устройства). Распределение задач в группе мобильных роботов – нетривиальный процесс, направленный на определение и оперативную оптимизацию ресурсов группы, обеспечивающих достижение групповой цели. Для принятия решений по распределению задач необходимо построение причинно-следственных связей между событиями, возникающими в группе. Одним из классических подходов решения данной задачи является использование методов классической оптимизации, предусматривающих исследование непрерывной функции многих переменных на экстремум, для анализа приращений значений происходящих событий по отношению к множеству приращений индикаторов процесса. Но решение при помощи подобного подхода не всегда является целесообразным из-за чрезмерных вычислительных затрат и высокого количество итераций, обусловленных большой размерностью вектора состояния исследуемого процесса. В качестве альтернативного подхода решения подобных задач является использование аппарата искусственных нейронных сетей [3–5].
Целью работы является разработка интеллектуального метода распределения задач в группе мобильных роботов на основе нейронных сетей, с помощью которого возможно эффективно реализовать процесс распределения и обеспечить надежность функционирования роботов в условиях дефицита ресурсов. Для решения поставленной цели предлагается использовать современные методы моделирования, теории управления и искусственного интеллекта на основе нейронных сетей.
Рассмотрим задачу выполнения заданий роботами на рабочем поле размером N×N. Пусть задано n роботов, которым необходимо выполнить задачи Vi из массива заданий V, при этом задачи не связаны между собой. Для каждого робота определим его функциональные возможности Fi. В начальный момент времени роботы располагаются в точках с координатами (xi, yi), где i = 1, 2, …, N. Примем, что показателем качества qi выполнения задания является функционал
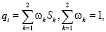
где ωk = const ∈ [0, 1] – весовые коэффициенты, Sk – функции соответствия, вычисляемые для оценки степени соответствия потенциального решения k-му критерию.
Функция S1 характеризует критерий качества выполнения задания в соответствии с длиной траектории:
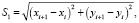
где (xi+1, yi+1) – координаты точки, в которой необходимо выполнить задание.
Функция S2 характеризует критерий качества выполнения задания в соответствии с функционалом робота:
S2 = Fi.
Процесс оптимального распределения задач будет заключаться в поиске критерия Q:
Q = min {q1, q2,…, qn}.
Найденное решение Q обеспечивает минимизацию пройденного расстояния и выбор робота в соответствии с требуемым функционалом, что будет способствовать экономии и оптимизации ресурсов.
Рассмотрим группу гетерогенных мобильных роботов, выполняющих операции на некотором участке рабочего пространства. При этом каждый из них имеет возможность выполнить ограниченный набор операций (для некоторых роботов часть запланированных задач является невыполнимой). Также следует учесть, что некоторые простые задачи нецелесообразно назначать роботам, которые имеют расширенный набор функций, при наличии на равном с ними удалении роботов с меньшим набором функций. Например, если на некоем расстоянии от объекта располагаются два робота R1 и R2, при этом робот R1 может выполнять измерения, расчеты, видеосъемку и анализ состояния объекта, а робот R2 – только видеосъемку объекта. При таком расположении роботов в группе, если ставится задача провести видеосъемку, целесообразнее использовать робота R2, так как в последующий момент времени может возникнуть задача, которую способен выполнить только R1, но не сможет выполнить R2. В противном случае задача не будет выполнена или появится необходимость привлекать третьего робота R3, который может находиться на значительном удалении, что, в итоге, приведет к нецелесообразной трате ресурсов. Задачи, решаемые роботами как потенциальными агентами, могут частично дублироваться, но если один из них функционально перегружен, а другой выполняет лишь одну функцию (например, видеосъемку), его использование может являться целесообразным по показателям надежности или массогабаритным характеристикам.
Роботы получают сигналы управления из командного центра, который принимает решение о распределении задач и выборе робота для их выполнения. В процессе взаимодействия с командным центром используется специализированный протокол, в соответствии с которым роботы сообщают о начале, окончании и о невозможности выполнения задачи, а также координаты своего местонахождения. В соответствии с данным протоколом робот при изменении своего статуса или окружающей обстановки отправляет сообщение в центр управления, например отправляется сообщение «задача выполнена» после отработки определенного задания или «координаты местонахождения X, Y» при перемещении робота в новую точку рабочего пространства в соответствии с поставленным заданием.
В ходе выполнения операций основными функциями командного центра являются анализ данных и распределение задач в соответствии со следующими условиями:
1) задача (последовательность операций) должна быть выполнена;
2) временные затраты для выполнения задачи должны быть минимальны;
3) материальные (энергетические) затраты должны быть минимальны;
Необходимо синтезировать алгоритм распределения задач в соответствии с перечисленными условиями (ограничениями) и критериями оптимальности. В качестве решения предлагается использовать нейронную сеть прямого распространения, которая позволяет реализовать однонаправленную передачу сигналов из командного центра отдельным роботам группы. Использование такой сети обусловлено простотой реализации, быстротой выработки сигналов управления, а также гарантированным получением ответа после прохождения данных по слоям. Выбранная нейронная сеть функционирует в режиме без обратной связи и формирование команд происходит при помощи прямых каналов связи с явным заданием значения команды.
Реализация алгоритма
Синтезируется нейронная сеть, имеющая классическую структуру персептрона – входные, скрытые и выходные нейроны, связанные между собой синапсами, имеющими определенный вес. Структура сети состоит из элементов трех типов: S-элементов, A-элементов и одного R-элемента. Вес синапса задается при начальном обучении нейронной сети в зависимости от того, какой робот передает информацию входному нейрону. В предлагаемом варианте нейронной сети веса будут распределены таким образом:
1) W1, W2, …, Wk где Wk – вес, назначенный синапсу, соединяющему первый из тройки входной и скрытый нейрон, отвечающий за набор функций, где k – максимальное значение набора функций, то есть полный ее набор;
2) S1, S2, …, Sn, где Sn – вес, назначенный синапсу, соединяющему второй из тройки входной и скрытый нейрон, отвечающий за удаленность от места выполнения задачи, n в данном случае – максимальная удаленность;
3) A1, A2 – веса, назначенные синапсам, соединяющим третий из тройки входной и скрытый нейрон, отвечающий за возможность выполнения задачи, где A1 – возможность выполнения задачи, A2 – невозможность выполнения задачи.
Q – это вес, назначенный синапсу, соединяющему скрытый и выходной нейроны, и являющийся показателем целесообразности назначения задачи тому или иному роботу по заданному алгоритму, описанному ниже; R – вес, назначенный синапсу, соединяющему выходной нейрон и центр управления, указывающий, какой из скрытых нейронов обслуживает робота, которому целесообразно назначить текущее задание.
Входные нейроны разделены по группам: первая отвечает за сбор данных о наборе функций робота; вторая – за сбор данных о его позиции в системе координат; третья – за сбор данных о возможности или невозможности выполнения задачи. Роботы, находящиеся в рабочем пространстве, могут перемещаться, соответственно, они будут прикрепляться к другим, обслуживающим их, тройкам входных нейронов и будет происходить переобучение входных синапсов. Каждый робот обслуживается тремя нейронами входной группы, при этом входные нейроны изменяют состояние (вес) синапса, исходящего от них в зависимости от данных, полученных от соответствующего робота. Далее вычисляется вес синапса, исходящего из скрытого нейрона:
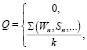
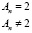 ,
,
где k – количество суммируемых весов.
В качестве примера для первого робота выберем: W1 = 5, S1 = 3, A1 = 1. Выполняется условие Аn ≠ 2, соответственно Q1 в сети на участке, обслуживающем его, будет равняться (3 + 5)/2 = 4. Для второго робота W2 = 7, S2 = 2, A2 = 1. Выполняется условие Аn ≠ 2, поэтому Q2 = (2 + 7)/2 = 4,5. Для третьего робота W3 = 1, S3 = 1, A3 = 2. Т.к. Аn = 2, робот не способен выполнить поставленную задачу.
Далее информация поступает на выходной нейрон, вес синапса которого формируется исходя из наименьшего веса входящих в него синапсов. В настоящем алгоритме вес синапса, соединяющего выходной нейрон с входными, будет равен среднему арифметическому весов, входящих в скрытый нейрон. Так как Q1 = 4, Q2 = 4,5, Q3 = 0, то в результате, если наименьший вес входящего синапса скрытого нейрона будет равен 1, то вес синапса выходного нейрона R = 1.
Фактически нейронная сеть, состоящая из входных, скрытых и выходных нейронов, будет обучаться анализу текущей обстановки и формированию выводов о целесообразности назначения конкретному роботу текущей задачи. Тройки входных нейронов в режиме реального времени получают от роботов информацию об их местонахождении, текущей функциональности и возможности выполнения конкретной задачи. В предлагаемом варианте параметры нейронной сети могут также корректироваться администратором путем назначения дополнительных коэффициентов. В этом случае Q1, для которого выполняется условие Аn ≠ 2, может быть вычислен по формуле
Q1 = wW1 + sS1 + aA1,
где w, s, a – дополнительные коэффициенты.
Дополнительные коэффициенты позволяют скорректировать значимость того или иного критерия, что предоставляет оператору возможность компенсировать небольшие изменения окружающей среды и снижение эффективности роботов в процессе эксплуатации без полного переобучения нейросети.
Обучающая выборка для предлагаемого варианта нейронной сети представляет собой упорядоченный набор значений удаленности робота от места выполнения задачи, его функциональности и рассчитанного показателя качества Q.
Целью алгоритма является поиск робота, который выполнит поставленную задачу при минимально возможном значении показателя качества Q (вес выходного синапса).
На вход нейронной сети подаются данные в десятичном виде (в аппаратной реализации – импульсы определенной формы), которые являются обучающей выборкой. Используемая в настоящем исследовании нейронная сеть обладает свойством обучения без учителя, в качестве обучающей выборки выступают предобработанные данные. Для оптимальной работы персептрона все входные сигналы нормализованы в промежутке [0; 1]. Обучение нейронной сети происходит за счет перемещения роботов по участкам, каждый из которых закрепляется за конкретным нейроном входного слоя. Также у отдельных роботов могут изменяться параметры функционирования без изменения координат, – например, изменение функционала Fi в результате возникновения неисправности или другой нештатной ситуации с потерей определенной функции. В этом случае значение функционала меняется на Fi-1 и происходит переобучение нейронной сети.
Программная модель и результаты
Для реализации предложенного подхода был разработан вычислительный алгоритм в среде Matlab на примере группы, состоящей из четырех роботов. Каждый робот имеет свой уникальный набор функций, при этом для части роботов некоторые задачи являются невыполнимыми. Сигналы управления поступают из командного центра, осуществляющего анализ данных и распределение задач. Роботы могут передвигаться, выполняя задания, назначаемые командным центром на дискретном рабочем поле, каждая задача характеризуется номером и координатами клетки, в которой она должная быть выполнена.
Исходные данные для моделирования приведены в табл. 1, 2.
Таблица 1
Конфигурация роботов на рабочем поле
|
Робот, № |
Координаты |
Функционал |
|
1 |
(2; 3) |
1,2 |
|
2 |
(5; 3) |
1,2 |
|
3 |
(3; 7) |
3 |
|
4 |
(6; 5) |
4 |
Таблица 2
Конфигурация целевых точек на рабочем поле
|
Целевая точка, № |
Координаты |
Функционал в точке |
|
1 |
(6; 8) |
1 |
|
2 |
(1; 6) |
2 |
|
3 |
(3; 1) |
3 |
|
4 |
(7; 2) |
4 |
На рисунка в графической форме показана исходная конфигурация рабочего поля, где обозначено Рk(i) – расположение k-го робота с набором функций i; Цk(i) – расположение целевой точки, в которой необходимо выполнить задание роботом с функционалом i.
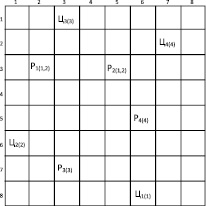
Исходная конфигурация рабочего поля
Модель персептрона реализована со следующими параметрами:
– количество нейронов в скрытом слое: 5;
– число итераций: 500;
– длина тестовой выборки: 50;
– размерность обучающей выборки: 328.
В табл. 3 приведены результаты работы программы с количественными характеристиками значений показателя качества Qk распределения задач для k-го робота.
Таблица 3
Количественные характеристики распределения задач
|
Цель 1 |
Цель 2 |
Цель 3 |
Цель 4 |
|
|
Q1 |
3,16 |
1,08 |
– |
– |
|
Q2 |
2,53 |
2,94 |
– |
– |
|
Q3 |
– |
– |
2,6 |
– |
|
Q4 |
– |
– |
– |
0,95 |
Из табл. 3 согласно условию выбора Qi = min(Q1, Q2, Q3, Q4) распределение задач осуществляется в следующем порядке: целевая задача № 1 выполняется роботом № 2, целевая задача № 2 – роботом № 1, целевая задача № 3 – роботом № 3, целевая задача № 4 – роботом № 4.
Таким образом, разработанная программа реализует структуру нейронной сети и позволяет провести программные эксперименты по моделированию процесса распределения задач для различных входных данных и наборов параметров (критериев), при этом результаты моделирования представляются как в текстовой (директивной) форме, так и в графическом окне, отражающем расположение роботов в рабочем пространстве.
Нейронная сеть способна выявлять скрытые связи между входными и выходными переменными, что позволяет находить решение сложных задач, которые эксперт и тем более аналитические методы решают недостаточно точно. Поэтому в дальнейшем предложенный алгоритм планируется модифицировать с использованием дополнительных критериев оптимальности со скрытыми связями между входными и выходными переменными.
Заключение
В статье рассмотрена методика синтеза интеллектуального алгоритма распределения задач в группе мобильных роботов. В качестве примера рассмотрена группа из четырех роботов. Следует отметить, что центр управления способен обслуживать достаточно большие группы роботов, размер которых ограничен его вычислительными мощностями и доступными объемами запоминающих устройств. Предлагаемая нейронная сеть также не ограничивает количество групп роботов, на которые будет распространяться процесс управления.
Несомненным преимуществом данной методики является то, что администратор сети может на этапе ввода обучающей выборки назначить повышающий или понижающий коэффициент одному из весов, тем самым указать, насколько важен для распределения задачи тот или иной параметр. Также стоит отметить, что данный метод отличается универсальностью, в рамках его реализации могут быть добавлены другие критерии, на основе которых будет производиться распределение задач.
Работа поддержана грантом РФФИ № 16-29-04165-офи_м и Программой Президиума РАН № I.29П.
Библиографическая ссылка
Даринцев О.В., Мигранов А.Б. ИНТЕЛЛЕКТУАЛЬНОЕ РАСПРЕДЕЛЕНИЕ ЗАДАЧ В ГРУППЕ МОБИЛЬНЫХ РОБОТОВ // Современные наукоемкие технологии. 2019. № 5. С. 30-34;URL: https://top-technologies.ru/ru/article/view?id=37515 (дата обращения: 01.03.2026).



