Создание эффективных математических моделей сигналов, распространяющихся в каналах передачи информации, подверженных случайным воздействиям, в настоящее время весьма актуально. Эти модели необходимы для предсказания ожидаемых искажений в пространственной и временной структуре сигналов и для мониторинга состояния каналов по характеристикам пробных зондирующих сигналов. Рассматривая канал как возмущенную динамическую систему, можно получить приближенные аналитические соотношения между флуктуационными характеристиками сигнала и параметрами случайных воздействий. Последующая алгоритмизация этих соотношений позволяет выполнить численное моделирование статистических характеристик сигнала при распространении в канале. Используя универсальность численных алгоритмов [1] и простоту получения приближенных аналитических соотношений, можно проводить исследование характеристик сигнала в широком классе возмущений параметров информационного канала. С другой стороны, обращение функциональных соотношений между характеристиками сигнала и параметрами канала позволяет получить оперативную информацию о состоянии канала.
В работе [2] нами была предложена схема оперативной алгоритмизации численно-аналитических расчетов флуктуаций фазы и направления распространения сигнала в стохастическом неоднородном канале. Для прогнозирования оптимальных условий прохождения сигнала через возмущенный канал важно также иметь информацию о флуктуациях его групповой задержки. Ранее в работе [3] были получены аналитические выражения для пространственных автокорреляционных функций группового пути и времени группового запаздывания сигнала, распространяющегося в ионосферном радиоканале, средняя диэлектрическая проницаемость которого изменялась по линейному закону. Для решения ряда практических задач необходимо, чтобы функция диэлектрической проницаемости невозмущенного канала могла быть описана более общими аналитическими моделями высотных профилей. Также для практики требуется использование моделей, которые задают диэлектрическую проницаемость канала в виде дискретных данных с последующей сплайн-интерполяцией этих данных для обеспечения непрерывности производных первого и второго порядка, необходимых в расчетах.
Цель работы заключается в создании оперативной схемы алгоритмизации численно-аналитических расчетов флуктуаций группового времени задержки сигнала при распространении в случайно-неоднородном канале, средний высотный профиль диэлектрической проницаемости которого задан произвольной аналитической функцией.
Вывод основных теоретических соотношений
В лучевом приближении групповую задержку сигнала можно определить, вычисляя стохастический интеграл по траектории, связывающей корреспондентов [4]:
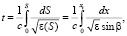 (1)
(1)
где ε – случайная функция диэлектрической проницаемости канала, с – скорость света в вакууме, β – угол рефракции луча, dS – элемент дуги, xt – координата пункта приёма сигнала. Определим флуктуацию групповой задержки сигнала в первом приближении метода возмущений [5, 6]. Введем разложения:
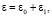 (2)
(2)
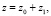 (3)
(3)
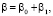 (4)
(4)
где ε0, z0, β0 – соответственно диэлектрическая проницаемость и траекторные характеристики сигнала в невозмущенном канале; ε1, z1, β1 – возмущение диэлектрической проницаемости канала и флуктуации траекторных характеристик сигнала.
Считая 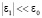 , решение (1) будем искать в виде: t = t0 + t1. Подставляя разложения (2)–(4) в формулу (1) и проводя асимптотические разложения, в первом приближении для флуктуации групповой задержки получаем
, решение (1) будем искать в виде: t = t0 + t1. Подставляя разложения (2)–(4) в формулу (1) и проводя асимптотические разложения, в первом приближении для флуктуации групповой задержки получаем
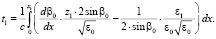 (5)
(5)
Важно отметить, что флуктуация траектории z1(x), входящая в подынтегральное выражение (5), должна удовлетворять двухточечным краевым условиям: z1(0) = z1(xt) = 0. Сделаем в (5) замену переменной 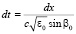 . С учетом формы лучевых уравнений [2], получаем
. С учетом формы лучевых уравнений [2], получаем
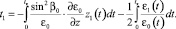 (6)
(6)
где tк – групповая задержка сигнала в невозмущенном канале в пункте приема xt.
Для вычисления (6) используем выражение для флуктуации траектории, полученное при решении двухточечной траекторной задачи [2]:
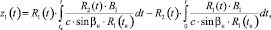 (7)
(7)
где βн – угол входа луча в канал (относительно вертикали),
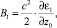
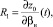
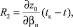 (8)
(8)
Подставляя формулу (7) в (6), имеем
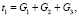 (9)
(9)
где
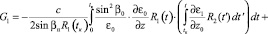 (10)
(10)
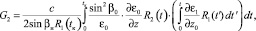 (11)
(11)
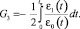 (12)
(12)
Интегралы (10), (11) вычислим методом интегрирования по частям [7]. Учитывая двухточечные краевые условия для флуктуаций траектории, получаем
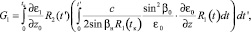 (13)
(13)
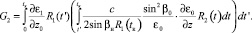 (14)
(14)
Подставляя (12)–(14) в (9), имеем:
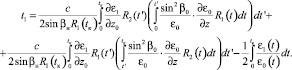 (15)
(15)
Введём переобозначения:
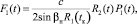 (16)
(16)
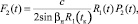 (17)
(17)
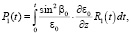
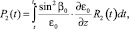
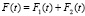 . (18)
. (18)
С учетом (16)–(18), формула (15) принимает вид
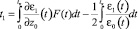 . (19)
. (19)
Заметим, что выражение (19) удобно для составления статистических моментов флуктуации времени группового запаздывания сигнала, поскольку функция F(t) не содержит флуктуаций траекторных характеристик сигнала и случайных возмущений диэлектрической проницаемости канала. В частности, используя (19), для дисперсии групповой задержки имеем
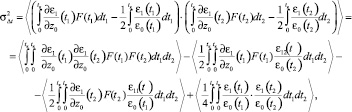 (20)
(20)
где 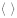 – знак усреднения по ансамблю неоднородностей.
– знак усреднения по ансамблю неоднородностей.
Для вычисления (20) необходимо задать функцию пространственной корреляции флуктуаций диэлектрической проницаемости канала. Используя метод суммарно-разностного интегрирования [4], в случае квазиоднородного случайного поля неоднородностей канала и гауссова корреляционного эллипсоида получаем
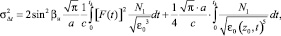 (21)
(21)
где a – масштаб неоднородностей, N1 – неоднородная часть корреляционной функции, а интегрирование проводится по суммарной переменной t = (t1 + t2)/2. При выводе (21) предполагалось, что функция N1 меняется медленно по сравнению с изменениями гауссова корреляционного эллипсоида.
Полагая предел tк переменной величиной, интегральное выражение (21) можно представить в дифференциальной форме. Объединяя полученные дифференциальные уравнения с системой невозмущенных лучевых уравнений [2], продифференцированной по свободному параметру βн, а также с самой системой невозмущенных лучевых уравнений, получаем полную систему дифференциальных уравнений для одновременного расчета средней траектории и дисперсии группового времени задержки сигнала в информационном канале:
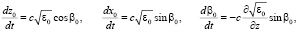
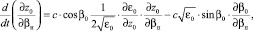
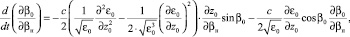
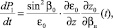
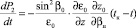
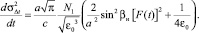 (22)
(22)
Результаты математического моделирования и их обсуждение
Для демонстрации работы предложенной схемы алгоритмизации на рис. 1, 2 приведены результаты численных расчетов на основе системы (22) среднеквадратичного отклонения группового пути сигнала 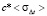 , связанного с дисперсией групповой задержки соотношением:
, связанного с дисперсией групповой задержки соотношением: 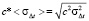 . Расчеты представлены в зависимости от рабочей частоты и угла входа сигнала в ионосферный декаметровый радиоканал (
. Расчеты представлены в зависимости от рабочей частоты и угла входа сигнала в ионосферный декаметровый радиоканал (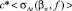 ). Модель ε0 задавалась в виде
). Модель ε0 задавалась в виде
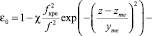
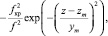 (23)
(23)
где zme, zm, yme, ym, fкре, fкр – высоты максимумов электронной концентрации, полутолщины и критические частоты ионосферных слоев E и F2 соответственно; f – рабочая частота; параметр χ позволяет включить (исключить) слой E. Неоднородная часть корреляционной функции представлялась зависимостью: 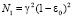 , где γ2 – интенсивность неоднородностей электронной концентрации. Параметры моделей составляли: zme = 125 км, yme = 25 км, fкре = 3 МГц, zm = 300 км, ym = 100 км, fкр = 6 МГц, γ2 = 0,008, а = 10 км, f = 6÷30 МГц. Параметр χ принимал значения 0 и 1. Из рис. 1 следует, что в частотно-угловых зависимостях среднеквадратичного отклонения группового пути сигнала при распространении в однослойном (χ = 0) ионосферном радиоканале имеются области повышенных значений. Возрастание флуктуаций группового пути связано с увеличением ионосферного участка рассеяния сигнала при отражении вблизи максимума ионизации слоя F2. На более высоких рабочих частотах максимумы
, где γ2 – интенсивность неоднородностей электронной концентрации. Параметры моделей составляли: zme = 125 км, yme = 25 км, fкре = 3 МГц, zm = 300 км, ym = 100 км, fкр = 6 МГц, γ2 = 0,008, а = 10 км, f = 6÷30 МГц. Параметр χ принимал значения 0 и 1. Из рис. 1 следует, что в частотно-угловых зависимостях среднеквадратичного отклонения группового пути сигнала при распространении в однослойном (χ = 0) ионосферном радиоканале имеются области повышенных значений. Возрастание флуктуаций группового пути связано с увеличением ионосферного участка рассеяния сигнала при отражении вблизи максимума ионизации слоя F2. На более высоких рабочих частотах максимумы 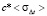 смещаются в область больших углов входа сигнала в канал, так как условия пробоя ионосферы возникают уже внутри канала на высотах ниже уровня максимальной ионизации. Уменьшение максимальных значений флуктуаций на высоких частотах связано с дисперсионными свойствами ионосферы. Учет нижележащей ионизации ионосферы (χ = 1) приводит к дополнительному максимуму среднеквадратичного отклонения группового пути сигнала (рис. 2), так как появляется возможность пробоя сигнала сквозь ионосферный слой E.
смещаются в область больших углов входа сигнала в канал, так как условия пробоя ионосферы возникают уже внутри канала на высотах ниже уровня максимальной ионизации. Уменьшение максимальных значений флуктуаций на высоких частотах связано с дисперсионными свойствами ионосферы. Учет нижележащей ионизации ионосферы (χ = 1) приводит к дополнительному максимуму среднеквадратичного отклонения группового пути сигнала (рис. 2), так как появляется возможность пробоя сигнала сквозь ионосферный слой E.
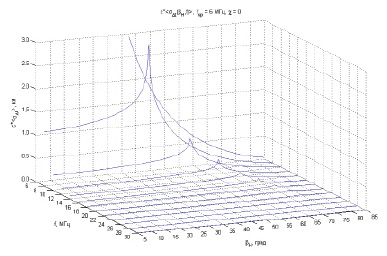
Рис. 1. Частотно-угловые зависимости среднеквадратичных отклонений группового пути сигнала в случайно-неоднородном ионосферном радиоканале с диэлектрической проницаемостью, заданной однослойной моделью
Рис. 2. Среднеквадратичные отклонения группового пути сигнала в ионосферном радиоканале с учетом нижележащего слоя Е
Заключение
Предложена схема алгоритмизации расчетов стохастического интеграла по траектории для флуктуаций группового времени задержки и группового пути сигнала в случайно-неоднородном информационном канале. На основе метода возмущений получена аналитическая интегральная формула для отдельной реализации флуктуаций групповой задержки сигнала в канале. В отличие от расчетов флуктуаций фазы сигнала, когда в первом приближении метода возмущений интегрирование проводится по невозмущенной траектории, при расчетах флуктуаций группового запаздывания учтены флуктуации траектории. Для расчета траекторных флуктуаций, входящих в интегральную формулу, использованы результаты решения стохастической траекторной задачи с двухточечными краевыми условиями. Выполнены аналитические преобразования, позволяющие привести стохастический интеграл к виду, удобному для составления статистических моментов групповой задержки сигнала. Для описания поля случайных неоднородностей канала использованы представления о пространственном корреляционном эллипсоиде. Получено интегральное выражение для дисперсии флуктуаций группового времени задержки в канале передачи сигнала. Выражение для дисперсии задержки сведено к системе обыкновенных дифференциальных уравнений первого порядка. Получена полная система дифференциальных уравнений для одновременного численного расчета дисперсии групповой задержки и средней траектории сигнала в случае произвольного высотного профиля средней диэлектрической проницаемости случайно-неоднородного канала. Показана эффективность предложенной схемы алгоритмизации расчетов стохастического интеграла по траектории в задаче моделирования частотно-угловых зависимостей среднеквадратичных отклонений группового пути сигнала в ионосферном радиоканале.
Библиографическая ссылка
Агеева Е.Т., Афанасьев Н.Т., Ким Д.Б., Медведева О.И., Чудаев С.О. ЧИСЛЕННО-АНАЛИТИЧЕСКАЯ АЛГОРИТМИЗАЦИЯ РАСЧЕТОВ ФЛУКТУАЦИЙ ГРУППОВОГО ВРЕМЕНИ ЗАДЕРЖКИ В КАНАЛАХ ПЕРЕДАЧИ СИГНАЛОВ // Современные наукоемкие технологии. 2019. № 5. С. 9-14;URL: https://top-technologies.ru/ru/article/view?id=37511 (дата обращения: 31.01.2026).



