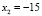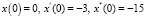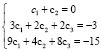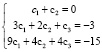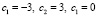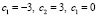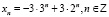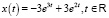Линейные дифференциальные и рекуррентные уравнения – едва ли не единственный класс уравнений, для которых имеется полная теория. Эта теория является ветвью линейной алгебры и излагается в том или ином объеме во всех технических вузах. Однако ее преподавание проводится, как правило, в разных дисциплинах. Целью настоящей статьи является анализ возможностей и особенностей реализации единого подхода преподавания теории дифференциальных и рекуррентных уравнений в курсе высшей математики в двух последовательно идущих темах. В центральной части статьи дается краткий обзор основных положений общей теории, отмечаются аналогии и возможные подходы к изложению элементов теории. В заключении обсуждаются методические особенности изложения материала и педагогическая целесообразность такого подхода.
Линейные однородные уравнения
Рассмотрим для начала линейное однородное рекуррентное уравнение с постоянными коэффициентами k-го порядка
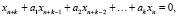 (1)
(1)
здесь 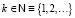 – фиксировано,
– фиксировано, 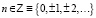 , которое также будем называть дискретным, и линейное однородное дифференциальное уравнение с постоянными коэффициентами k-го порядка
, которое также будем называть дискретным, и линейное однородное дифференциальное уравнение с постоянными коэффициентами k-го порядка
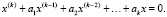 (2)
(2)
В уравнениях (1) и (2) a1, a2,.., ak – постоянные вещественные числа (коэффициенты). В уравнении (2) 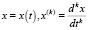 .
.
Замечание 1. Следует отметить, что во многих учебных пособиях полагают 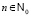 , что является не совсем точным по отношению к линейному однородному уравнению с постоянными коэффициентами. Полагая
, что является не совсем точным по отношению к линейному однородному уравнению с постоянными коэффициентами. Полагая 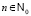 , мы определяем только положительную траекторию, а не целую, которая получается при
, мы определяем только положительную траекторию, а не целую, которая получается при 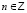 .
.
Замечание 2. Уравнения вида (1) в технических приложениях часто записывают в виде
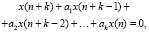
тем самым подчеркивается факт зависимости переменной x от дискретного времени t = n.
Как хорошо известно, решением уравнения (1) называется функция 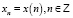 , т.е. числовая последовательность, удовлетворяющая при всех целых значениях аргумента
, т.е. числовая последовательность, удовлетворяющая при всех целых значениях аргумента 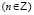 уравнению (1). Решением уравнения (2) называется функция x(t) вещественного аргумента
уравнению (1). Решением уравнения (2) называется функция x(t) вещественного аргумента 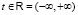 , обращающая уравнение (2) в тождество. Заметим при этом что уравнения (1) и (2) всегда имеют тривиальные (нулевые) решения
, обращающая уравнение (2) в тождество. Заметим при этом что уравнения (1) и (2) всегда имеют тривиальные (нулевые) решения
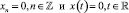 .
.
Уравнения (1) и (2) обладают следующими свойствами:
Если xn – решение (1), то 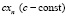 – решение (1). Если x(t) – решение (2), то сx(t) – также решение (2). Если
– решение (1). Если x(t) – решение (2), то сx(t) – также решение (2). Если 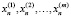 – решения (1), то
– решения (1), то 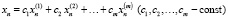 – решение (1). Если
– решение (1). Если 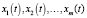 – решения (2), то
– решения (2), то 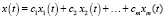 – решение уравнения (2).
– решение уравнения (2).
В теории уравнений (1) и (2) важное место занимают следующие утверждения, формулируемые обычно в виде лемм, т.е. вспомогательных утверждений.
Лемма 1. Если 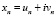 – комплексное решение рекуррентного уравнения (1), то вещественные числовые последовательности un и vn – будут решениями (1).
– комплексное решение рекуррентного уравнения (1), то вещественные числовые последовательности un и vn – будут решениями (1).
Аналогичное утверждение имеет место для уравнения (2).
Лемма 2. Если 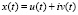 – комплексное решение дифференциального уравнения (2), то вещественные функции u(t) и v(t) – будут решениями (2).
– комплексное решение дифференциального уравнения (2), то вещественные функции u(t) и v(t) – будут решениями (2).
Фундаментальную роль в теории уравнений (1) и (2) играют следующие теоремы.
Теорема 1. Если решения уравнения (1) 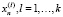 – линейно независимы (это понятие мы здесь не обсуждаем, считая его известным [1]), то во множестве всех решений они образуют базис, то есть все решения (1) находятся в формуле
– линейно независимы (это понятие мы здесь не обсуждаем, считая его известным [1]), то во множестве всех решений они образуют базис, то есть все решения (1) находятся в формуле
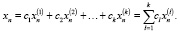 (3)
(3)
Здесь 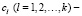 произвольные числа.
произвольные числа.
Теорема 2. Если решения 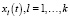 – линейно независимы, то во множестве всех решений уравнения (2) они образуют базис и все решения уравнения (2) находятся в формуле
– линейно независимы, то во множестве всех решений уравнения (2) они образуют базис и все решения уравнения (2) находятся в формуле
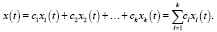 (4)
(4)
Таким образом, как в случае уравнения (1), так и в случае уравнения (2), для нахождения общего решения требуется найти фундаментальную систему решений 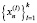 или
или 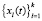 . Главное, что объединяет уравнения (1) и (2), это общая структура совокупности всех решений, называемая общим решением, а также понятие базиса в пространстве решений. Обращаем внимание, что размерность этого базиса равна порядку исходного уравнения, то есть k. Из сказанного вытекает следующая фундаментальная теорема.
. Главное, что объединяет уравнения (1) и (2), это общая структура совокупности всех решений, называемая общим решением, а также понятие базиса в пространстве решений. Обращаем внимание, что размерность этого базиса равна порядку исходного уравнения, то есть k. Из сказанного вытекает следующая фундаментальная теорема.
Теорема 3. Совокупность всех решений однородного рекуррентного (дифференциального) уравнения образует линейное пространство.
Поиск фундаментальных систем решений уравнений (1) и (2) обнаруживает много аналогий, на которые следует обратить внимание. Ненулевые решения уравнений (1) и (2) разыскивают соответственно в видах
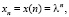 (5)
(5)
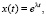 (6)
(6)
где λ – число подлежащее определению. Подстановка (5) и (6) в (1) и (2) приводит к одному и тому же алгебраическому уравнению, которое называется характеристическим:
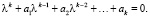
Часто корни характеристического уравнения называются в первом (дискретном) случае мультипликаторами, во втором (непрерывном) – характеристическими числами.
Как известно, характеристическое уравнение может иметь как вещественные (простые и кратные), так и комплексные (простые и кратные) корни (всего с учетом кратности k штук).
Пусть для определенности λ0 – простой вещественный корень. Ясно тогда, что решениями уравнений (1) и (2) будут функции
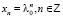 , (7)
, (7)
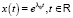 . (8)
. (8)
В общих решениях (3), (4) этим функциям будут отвечать соответственно слагаемые
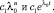
Если λ0 – вещественный корень кратности m, то, как известно, решениями будут следующие совокупности функций
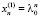 ,
, 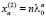 , … ,
, … , 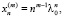 (9)
(9)
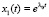 ,
, 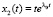 , … ,
, … ,
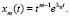 (10)
(10)
Точно так же как и в случае простого корня, в случае кратного корня λ0 в общем решении уравнений (1) и (2) будут отвечать слагаемые
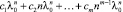
и
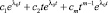
соответственно.
Аналогичным образом будет обстоять дело и в случаях комплексных кратных корней.
Пусть теперь 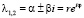 – простые комплексные корни характеристического уравнения. Тогда, применяя формулу Муавра и леммы 1, 2, получаем, что вещественными решениями уравнений (1) и (2) будут функции, структура которых следующая
– простые комплексные корни характеристического уравнения. Тогда, применяя формулу Муавра и леммы 1, 2, получаем, что вещественными решениями уравнений (1) и (2) будут функции, структура которых следующая
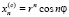 ,
, 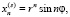 (11)
(11)
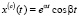 ,
, 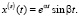 (12)
(12)
Для кратных корней 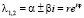 вещественными решениями уравнений (1) и (2) будут
вещественными решениями уравнений (1) и (2) будут
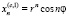 ,
, 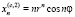 , … ,
, … ,
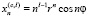 ,
,
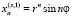 ,
, 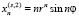 , …. ,
, …. ,
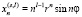 (13)
(13)
и
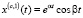 ,
, 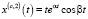 ,…,
,…,
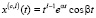 ,
,
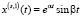 ,
, 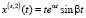 ,…,
,…,
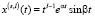 (14)
(14)
соответственно. Здесь l – кратность корней 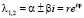 .
.
Совокупности решений (13) рекуррентного уравнения (1) в общем решении (3) будет соответствовать слагаемое
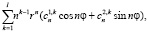
а совокупности решений (14) дифференциального уравнения (2) в общем решении (4) – соответственно слагаемое
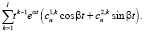
В последних формулах 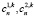 – произвольные постоянные.
– произвольные постоянные.
Для уравнения (1), так же как и для уравнения (2), ставится начальная задача (задача Коши): найти решение (частное решение), удовлетворяющее начальным данным:
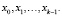 (15)
(15)
Для уравнения (2) начальные условия задаются k равенствами вида
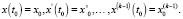 (16)
(16)
Здесь 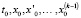 – заданные числа (начальные данные).
– заданные числа (начальные данные).
Поиск этих частных решений уравнений (1) и (2) приводит к решению линейных алгебраических систем относительно неизвестных c1, c2,…, ck, при этом в первом (дискретном) случае мы сталкиваемся с определителями Ван-дер-Монда и его обобщением – определителем Казорати и определителем Вронского.
Следует обратить внимание студентов, что начальная задача для уравнения (1) может быть поставлена с более общими начальными данными, например: 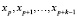 и обосновать это положение. Здесь p – любое число из множества
и обосновать это положение. Здесь p – любое число из множества 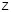 , играющее роль t0 в условиях (16). Учитывая постоянство коэффициентов однородных уравнений (1) и (2), можно всегда считать величины p и t0 нулями. Кроме того, номера
, играющее роль t0 в условиях (16). Учитывая постоянство коэффициентов однородных уравнений (1) и (2), можно всегда считать величины p и t0 нулями. Кроме того, номера 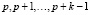 последовательности xn можно заменить любыми другими, главное, чтобы они были все различные и их количество равнялось k:
последовательности xn можно заменить любыми другими, главное, чтобы они были все различные и их количество равнялось k:
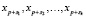 ,
,
где 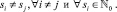
Пример 1. Рассмотрим теперь в параллель две модели (подобный наглядный пример необходимо рассмотреть в обязательном порядке):
|
Рекуррентное уравнение |
Дифференциальное уравнение |
|
|
|
|
Характеристическое уравнение |
|
|
|
|
|
Фундаментальная система решений |
|
|
|
|
|
Общее решение |
|
|
|
|
|
Начальные условия |
|
|
|
|
|
⇓ |
⇓ |
|
|
|
|
⇓ |
⇓ |
|
|
|
|
Решение задачи Коши |
|
|
|
|
Линейные неоднородные уравнения со специальной правой частью
Рассмотрим теперь линейные неоднородные уравнения
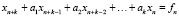 , (17)
, (17)
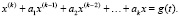 (18)
(18)
Здесь fn = f(n) – заданная числовая последовательность, g(t) – заданная функция 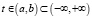 . Основное утверждение здесь определяется следующей теоремой.
. Основное утверждение здесь определяется следующей теоремой.
Теорема 4. Структура общих решений уравнений (17), (18) дается формулами
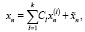 (19)
(19)
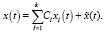 (20)
(20)
Здесь  – частные решения уравнений (17), (18) соответственно. Заметим при этом, что универсального метода нахождения частного решения
– частные решения уравнений (17), (18) соответственно. Заметим при этом, что универсального метода нахождения частного решения 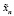 в формуле (19) нет, в отличие от метода нахождения решения
в формуле (19) нет, в отличие от метода нахождения решения 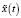 в (20).
в (20).
Хорошо известно, что в курсе дифференциальных уравнений в обязательном порядке рассматривается интегрирование уравнения (18) со специальной правой частью:
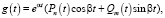
где Pn(t), Qm(t) – алгебраические полиномы степеней n и m; α и β – заданные константы (в приложениях такие функции играют огромную роль). При этом частное решение уравнения (18) разыскивают в виде
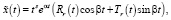
где Pr(t), Tr(t) – многочлены с неопределенными коэффициентами степени r = max{n, m}, а s = 0, если число α + βi не является корнем характеристического уравнения, если же α + βi является корнем характеристического уравнения, то s – кратность этого корня.
В теории рекуррентного уравнения (17) также можно рассмотреть несколько случаев специальной правой части с известными способами нахождения частных решений. Ограничимся здесь одним случаем (с другими можно ознакомиться по книге [2]):
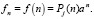
Здесь Pj(n) – заданный полином от n степени j, a – заданное число. Частное решение 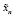 при этом разыскивают в виде
при этом разыскивают в виде
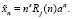
Обобщениями уравнений (17) и (18) являются уравнения
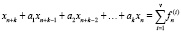 , (21)
, (21)
(здесь 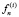 – заданная числовая последовательность с номером i),
– заданная числовая последовательность с номером i),
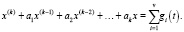 (22)
(22)
Теорема 5 (принцип суперпозиции). Общие решения уравнений (21), (22) имеют вид
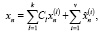 (23)
(23)
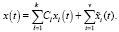 (24)
(24)
Здесь 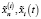 – частные решения (17), (18) с правыми частями
– частные решения (17), (18) с правыми частями 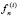 и gi(t) соответственно.
и gi(t) соответственно.
Таким образом, задача нахождения общих решений уравнений (21) ((22)) сводится к нахождению общего решения однородного уравнения и ν частных решений.
Замечание 3. Утверждение теоремы 5 играет фундаментальную роль в теории линейных колебаний, а также физике [3]. Это свойство линейных систем существенным образом отличает их от нелинейных.
Устойчивость тривиальных решений
Как уже отмечалось, однородные уравнения (1) и (2) имеют тривиальные решения, которым часто отвечают рабочие режимы функционирования технических систем. Эти решения обладают при определенных условиях на коэффициенты уравнений свойством притяжения всех других (нетривиальных) решений при n → +∞ и t → +∞. Отмеченное свойство называется асимптотической устойчивостью нулевого решения. Строгие определения мы здесь не приводим, отсылая читателя к специальной литературе [4]. Отметим при этом большое теоретическое значение теории устойчивости и ее значимость для приложений в современной технике. Справедлива следующая
Теорема 6 (об устойчивости). Если все корни характеристического уравнения находятся внутри единичного круга комплексной плоскости (рисунок, a), то все решения уравнения (1) обладают свойством xn > 0(n > +∞), то есть решение xn = 0 – асимптотически устойчиво; если в левой полуплоскости комплексных чисел (рисунок, б), то все решения уравнения (2) стремятся к нулю: x(t) > 0(t > +∞), то есть решение x(t) = 0 – асимптотически устойчиво.
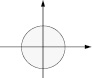
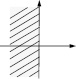
а) б)
Комплексные плоскости λ: a) рекуррентного уравнения; б) дифференциального уравнения
Линейные системы однородных уравнений
Изложенная выше теория естественным образом распространяется на системы линейных рекуррентных и дифференциальных уравнений с постоянными коэффициентами.
Рассмотрим для начала однородные линейные системы, записанные в векторной форме:
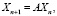 (25)
(25)
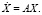 (26)
(26)
Здесь
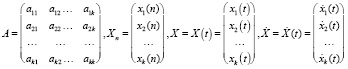 .
.
Непосредственная подстановка убеждает, что решениями систем (25) и (26) являются векторные функции
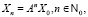 (27)
(27)
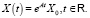 (28)
(28)
Здесь X0 – вектор начальных данных, eAt – матричная экспонента
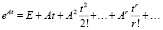 .
.
Совокупность всех решений векторных уравнений (25), (26) (общие решения) даются формулами 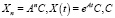 – произвольный постоянный k-мерный вектор.
– произвольный постоянный k-мерный вектор.
Замечание 3. Обращаем внимание, что если матрица А не особая 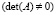 , то существует обратная A-1 и решением (25) будет
, то существует обратная A-1 и решением (25) будет 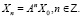
Замечание 4. Несмотря на то, что векторное уравнение (25) и его общее решение (27) имеют весьма простой вид, к такого рода уравнениям сводится достаточно широкий круг линейных задач, описывающих дискретные системы автоматического регулирования [5].
Заметим, что уравнения (1) и (2) могут быть записаны в виде систем (25), (26), при этом
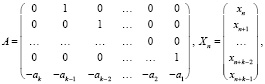

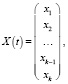 где
где 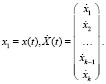
Найдем теперь базисные решения уравнений (25) и (26). Их будем разыскивать в виде
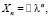 (29)
(29)
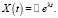 (30)
(30)
Здесь 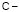 произвольный к-мерный вектор. Подстановка (29), (30) в (25), (26) приводит к уравнению
произвольный к-мерный вектор. Подстановка (29), (30) в (25), (26) приводит к уравнению
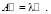 (31)
(31)
Таким образом, как в случае рекуррентной, так и в случае дифференциальной системы мы приходим к задаче на собственные значения и собственные векторы. Как известно, система уравнений (31) имеет нетривиальные решения при условии
 (32)
(32)
Уравнение (32) – характеристическое уравнение k-го порядка.
Далее мы ограничимся рассмотрением простейшего случая и наиболее важного с точки зрения приложений – случаем простого спектра матрицы A (спектром матрицы A называется совокупность ее собственных значений, спектр называется простым, если все корни характеристического уравнения (32) λ1, λ2,.., λk – различны).
Обозначим далее собственные векторы матрицы A, отвечающие собственным значениям λ1, λ2,.., λk через 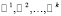 . Тогда справедлива следующая
. Тогда справедлива следующая
Теорема 7.
1. Векторные последовательности 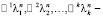 являются линейно независимыми решениями уравнения (25).
являются линейно независимыми решениями уравнения (25).
2. Совокупность всех решений уравнения (25) находится в формуле
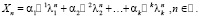 (33)
(33)
3. Векторные функции 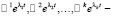 являются линейно независимыми решениями уравнения (26).
являются линейно независимыми решениями уравнения (26).
4. Совокупность всех решений уравнения (26) находится в формуле
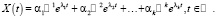 (34)
(34)
В (33) и (34) 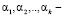 произвольные постоянные.
произвольные постоянные.
Пример 2. Следующее дискретное уравнение впервые было рассмотрено Леонардо Пизанским, более известным, как Фибоначчи, в начале XIII в.
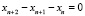 .
.
Последовательность, которая генерируется этим уравнением с начальными данными 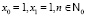 , носит сегодня его имя и описывает эволюционный процесс. Заметим, что в XIII веке не существовало отрицательных целых чисел, а физический смысл этой задачи был связан с образованием потомства от пары кроликов (c историей этой задачи можно ознакомиться в [6], а также многими интересными следствиями, которые можно вывести из этого уравнения). С другой стороны, наше уравнение, как нетрудно заметить, допускает в качестве решения двухстороннюю числовую последовательность вида: … –13, 8, –5, 3, –2, 1, –1, 0, 1, 3, 5, 8, 13, 21, … Таким образом, при определении всех решений уравнения Фибоначчи необходимо допустить, что
, носит сегодня его имя и описывает эволюционный процесс. Заметим, что в XIII веке не существовало отрицательных целых чисел, а физический смысл этой задачи был связан с образованием потомства от пары кроликов (c историей этой задачи можно ознакомиться в [6], а также многими интересными следствиями, которые можно вывести из этого уравнения). С другой стороны, наше уравнение, как нетрудно заметить, допускает в качестве решения двухстороннюю числовую последовательность вида: … –13, 8, –5, 3, –2, 1, –1, 0, 1, 3, 5, 8, 13, 21, … Таким образом, при определении всех решений уравнения Фибоначчи необходимо допустить, что 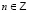 . Заметим при этом, что формула
. Заметим при этом, что формула
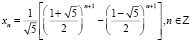 .
.
дает в качестве решения двухстороннюю числовую последовательность, приведенную выше.
Используя язык теории динамических систем, можно сказать, что последовательность 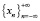 определяет целую траекторию, последовательность
определяет целую траекторию, последовательность 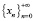 – положительную траекторию, а
– положительную траекторию, а 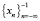 – отрицательную траекторию. Обозначим теперь
– отрицательную траекторию. Обозначим теперь
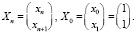
Тогда уравнение Фибоначчи можно записать в виде системы (25) с матрицей 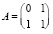 , решением которой будет векторная последовательность
, решением которой будет векторная последовательность
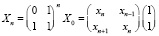 .
.
Линейные системы неоднородных уравнений
Рассмотрим теперь неоднородные системы с постоянными коэффициентами
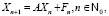 (35)
(35)
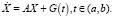 (36)
(36)
Здесь
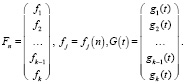
Решениями этих векторных уравнений будут функции
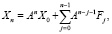 (37)
(37)
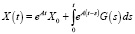 , (38)
, (38)
в чем легко убедиться простой подстановкой формул (37), (38) в уравнения (35), (36). Обратите внимание на единую структуру формул (37), (38).
Заключение
Хорошо известно, что, излагая тот или иной материал, преподаватель стремится постоянно поддерживать интерес к своему предмету, выбирать такую методику изложения, при которой достигается максимальный образовательный эффект. Когда учащиеся видят общность вводимых понятий, алгоритмов решения, единство подходов при изучении разных теорий, у них повышается интерес, расширяется кругозор и формируется настоящее знание. Опыт чтения лекций и проведения практических занятий по темам «Линейные дифференциальные уравнения с постоянными коэффициентами» и «Линейные рекуррентные уравнения» автором настоящей статьи привел его к заключению, что этот материал можно изложить последовательно в одном курсе. Для доказательства этого тезиса выше были приведены в конспективном виде основные положения из этих двух разделов математики, высказанные на общей теоретической платформе. Методика изложения указанных разделов должна быть общей и заключаться в строгом и последовательном использовании одинаковых обозначений и одних и тех же лексических понятий, к каковым относятся понятия: характеристическое уравнение, спектр, фундаментальная система решений, пространство решений и т.д. Таким образом, если реализовать указанную выше последовательность преподавания, эффект успешного усвоения этой общей теории будет значительно выше, чем при изложении этих вопросов разными преподавателями в разных курсах и с использованием разной лексики. Изложенный материал, естественно, не следует читать по приведенной выше схеме, т.е. буквально параллельно, так как это вызовет обратную реакцию – потерю интереса и непонимание в принципе несложных вещей. Обращаем также внимание на роль примеров при изложении материала, ибо сходство приемов нахождения частных и общих решений рассматриваемых уравнений аналогичны и играют важную разъяснительную роль. Эти аналогии переоценить нельзя и в процессе преподавания необходимо каждый раз их подчеркивать. И, наконец, педагогическая целесообразность такой последовательности изложения материала заключается в том, что многим студентам изучение дискретных структур дается проще, чем непрерывных. Часто преподаватель обнаруживает повышение активности ранее слабоуспевающего студента при изучении им рекуррентных уравнений. Разгадка здесь проста – такой студент осознает понятие дискретного времени лучше, чем непрерывного. Язык последовательностей для него является более естественным. Таким образом он может приобрести большой стимул к обучению и всей математики в целом. Наконец, мы надеемся, что преподаватели самостоятельно примут правильное решение в схеме изложения всего материала и расстановки необходимых дополнительных акцентов.
Библиографическая ссылка
Морозов А.В. ЛИНЕЙНЫE ДИФФЕРЕНЦИАЛЬНЫE И РЕКУРРЕНТНЫЕ УРАВНЕНИЯ ВО ВТУЗЕ // Современные наукоемкие технологии. 2019. № 4. С. 134-141;URL: https://top-technologies.ru/ru/article/view?id=37505 (дата обращения: 05.03.2026).
DOI: https://doi.org/10.17513/snt.37505




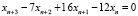
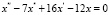
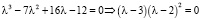
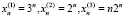
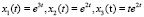
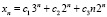
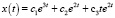
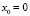 ,
, 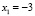 ,
,