Научный журнал

Современные наукоемкие технологии

ISSN 1812-7320

"Перечень" ВАК

ИФ РИНЦ = 0,940

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Заблоцкий В.Р. 1, 2 Луговской А.Е. 2

---

1 Московский государственный технический университет имени Н.Э. Баумана

2 Московский государственный университет геодезии и картографии

Рассмотрены особенности организации учебного курса по программированию на С++ в Московском университете геодезии и картографии (МИИГАиК). Курс по программированию характеризуется: использованием учебных компьютерных программ с геодезической тематикой, изучением языка С++ и общей геодезии в параллельном режиме, разработкой узкоспециализированных программ для учебных целей. Обсуждается код учебной программы для студентов картографов и геодезистов, изучающих основы программирования на языке С++. Программа вычисляет плоские прямоугольные координаты трех точек, заданных на листе топографической карты. Для вычисления координат используется прямая геодезическая задача. Рассчитанные значения координат сравниваются с измеренными координатами, и определяются погрешности Х и Y координат. Программа демонстрирует применение двумерных и одномерных массивов для хранения исходных и рассчитанных величин. Показано, как, используя оператор вычисления остатка от целочисленного деления, получить цикл с перебором всех элементов массива без повторного перезаписывания данных в массиве. Показано использование тригонометрических функций косинуса и синуса в цикле и их взаимное преобразование на основе счетчика цикла. Программа выводит на экран рассчитанные координаты точек и погрешности определения координат. Разработанная программа иллюстрирует решение прямой геодезической задачи для вычисления плоских прямоугольных координат множества заданных точек на основе применения технологии процедурного программирования.

Статья в формате PDF

0 KB

обучение программированию

учебная С++ программа

прямая геодезическая задача

вычисление прямоугольных координат точек

1. Прата С. Язык программирования С++. Лекции и упражнения. М.: ООО «И.Д. Вильямс», 2014. 1248 с.

2. Иванова Г.С. Основы программирования. М.: Изд-во МГТУ им. Н.Э. Баумана, 2014. 416 с.

3. Иванова Г.С., Ничушкина Т.Н., Пугачев Е.К. Объектно-ориентированное программирование. М.: Изд-во МГТУ им. Н.Э. Баумана, 2007. 368 с.

4. Либерти Дж., Кейденхед Р. Освой самостоятельно С++ за 24 часа. М.: ООО «И.Д. Вильямс», 2017. 448 с.

5. Дэвис С. С++ для чайников. М.: ООО «И.Д. Вильямс», 2016. 400 с.

6. Заблоцкий В.Р., Василева С.Ж. Многомодульная учебная программа, моделирующая измерение теодолитом расстояний, горизонтальных и вертикальных углов // Известия высших учебных заведений. Геодезия и аэрофотосъемка. 2018. Т. 62. № 6. С. 632–642.

Отметим некоторые особенности организации учебного курса по программированию на С++ в Московском университете геодезии и картографии (МИИГАиК). Обучение студентов программированию с геодезическим уклоном проводится на младших курсах параллельно с курсом общей геодезии. Поэтому желательно, чтобы компьютерные программы, используемые на занятиях по программированию, соответствовали той последовательности, в которой учебный материал излагается в курсе общей геодезии. Использование программ с решениями геодезических задач, не изученных студентами в базовом курсе геодезии, является малоэффективным. Кроме того, в процессе обучении программированию изучаемые конструкции языка должны рассматриваться в определенной последовательности. Это неизбежно приводит к тому, что преподаватель ограничен узким набором языковых конструкций, особенно на начальном этапе курса. Как результат, некоторые учебные программы содержат решения, реализованные не самым эффективным способом. Если понятие «оператор цикла» в курсе программирования изучается раньше понятия «функция», то в программах, иллюстрирующих циклы, нежелательно использовать функции, например тригонометрические функции или функции округления. Что не очень удобно и желательно учитывать при разработке учебных программ.

Целью данной работы является разработка типовых учебных компьютерных программ и заданий с геодезическим содержанием для обучения студентов – картографов и геодезистов основам программирования на языке С++.

Заметим, что обучение студентов программированию на С++ часто проводится по классическому учебнику С. Прата [1], учебникам Г.С. Ивановой и др. [2, 3], подготовленным в МГТУ им. Н.Э. Баумана, самоучителям Дж. Либерти и С. Дэвиса [4, 5]. Однако в настоящее время отсутствуют учебники по программированию, ориентированные на подготовку картографов и геодезистов. Нашей основной задачей [6] является разработка учебных программ. Эти программы не следует рассматривать как универсальные, предназначенные для обработки исходных геодезических данных в широком наборе комбинаций и при разных условиях. Программы для обучения студентов должны лишь иллюстрировать различные конструкции языка С++ на примере решения конкретных геодезических задач, может, даже и частных задач. Приведем пример, поясняющий сказанное. Известно, что прямая угловая засечка реализуется в геодезической практике, как правило, с дополнительным контрольным пунктом или в виде двукратной прямой засечки с уравниванием полученных данных. Однако если реализовать такую универсальную программу, то её код будет существенно превышать 50 строк и, как следствие, программа станет малопонятной и трудноусваиваемой для первоначального изучения. Поэтому учебные программы должны быть в основном небольшими (объемом до 50 строк), в тоже время охватывающими все разделы современного языка С++.

Материалы и методы исследования

Работа выполнена на персональном компьютере под управлением ОС Microsoft Windows 8.1. Для разработки программы использовалась среда программирования с открытым кодом Code:Blocks и компилятор GCC C++. Созданная программа запускается в командной строке, и результат выводит в командную строку.

В данной работе представлена учебная программа для студентов картографов и геодезистов, демонстрирующая использование прямой геодезической задачи при вычислении плоских прямоугольных координат трех точек, заданных на топографической карте. Рассмотрим геодезическую постановку задачи. Пусть даны три точки на топографической карте А(XА,YА), В(XB,YB) и С(XC,YC). Требуется определить их координаты по карте и вычислить эти же координаты на основе решения прямой геодезической задачи. Также необходимо сравнить вычисленные и измеренные координаты точек. Графическая часть задачи состоит в непосредственных измерениях на карте с помощью геодезического транспортира трех дирекционных углов направлений αA, αB, αC и трех расстояний d1, d2, d3 между точками с помощью линейки. Вычислительная часть задачи заключается в использовании формул для решения прямой геодезической задачи и вычислении по формулам координат точек. Прямоугольные X и Y координаты некоторой точки P вычисляются по формулам 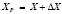и 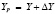, где ΔX и ΔY – значения приращения X и Y координат опорной точки, вычисляемые по формулам: 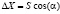, 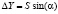и α – дирекционный угол направления. В таблице представлены данные вспомогательных измерений для вычисления координат искомых точек, а также результаты измерения этих же координат по карте. Координаты опорной точки выделены в таблице полужирным шрифтом.

Результаты исследования и их обсуждение

Разработанная программа вычисляет плоские прямоугольные координаты трех заданных на карте точек, используя двумерные и одномерные массивы координат точек, дирекционных углов направлений и расстояний между точками.

01: #include <iostream>

02: #include <iomanip>

03: #define Pi 3.141592653589793L

04:

05: using namespace std;

06: int main (void)

07: {

08: double measuredXYcoordinates[2][3] = {6066785,6067471,6067824,

08: 4311832, 4311549, 4312274};

09: double calculatedXYcoordinates[2][3] = { 0, 0, 0,

09: 0, 0, 0};

10: double errorXYcoordinates[2][3] = { 0, 0, 0,

10: 0, 0, 0 };

11: double gridAzimuth[2][3] = { 337, 63, 203, // градусы

11: 33, 54, 30 }; // минуты

12: double distance[3] = {738, 818, 1131}; // метры

13: double radian[3] = { 0, 0, 0};

14:

15: for(int j = 0; j < 3; j++) {

16: gridAzimuth[0][j] = gridAzimuth[0][j] + gridAzimuth[1][j]/60;

17: radian[j] = gridAzimuth[0][j] * Pi/180;

18: }

19: calculatedXYcoordinates[0][0] = measuredXYcoordinates[0][0];

20: calculatedXYcoordinates[1][0] = measuredXYcoordinates[1][0];

21: for(int i = 0; i < 2; i++)

22: for(int j = 1; j <= 3; j++)

23: calculatedXYcoordinates[i][j%3]=calculatedXYcoordinates[i][j-1]+

23: distance[j-1]*cos(i*Pi/2 - radian[j-1]);

24: for(int i = 0; i < 2; i++)

25: for(int j = 0; j < 3; j++)

26: errorXYcoordinates[i][j] = measuredXYcoordinates[i][j] -

26: calculatedXYcoordinates[i][j];

27: cout << fixed << setprecision(0);

28: char c; int j;

29: for( j = 0, c ='A'; j < 3; j++, c++){

30: cout << endl <<"Point "<< c << "\t\tX\t\t\tY" << endl;

31: for(int i = 0; i < 2; i++){

32: cout <<"Calculated: "<< calculatedXYcoordinates[i][j] << "\t";

33: }

34: cout << endl;

35: for(int i = 0; i < 2; i++){

36: cout <<"Measured: "<< measuredXYcoordinates[i][j] << "\t";

37: }

38: cout << endl;

39: for(int i = 0; i < 2; i++){

40: cout <<"Error:\t\t "<< showpos << errorXYcoordinates[i][j]

40: <<"\t" << noshowpos;

41: }cout << endl;

42: }

43: return 0;

44: }

Рассмотрим код программы. Инициализация массивов значениями координат Х и Y трех точек выполняется в строках 08-09. Причем массив измеренных координат Х и Y инициализируется значениями, считанными с топографической карты, массив вычисленных координат – нулевыми значениями. Эти два массива удобно представить в виде матриц размерности 2*3, в которых первая строка содержит Х-координаты, а вторая строка – Y-координаты точек. Здесь уместно напомнить, что в языках программирования С и С++ нумерация элементов массива начинается с нулевого индекса. Далее в строке 10 массив погрешностей errorXYcoordinates, вычисляемых как разность значений измеренных и вычисленных координат, инициализируется также нулевыми значениями. Массив gridAzimuth[2, 3] инициализируется значениями дирекционных углов, полученных по результатам угловых измерений на карте с помощью геодезического транспортира (строка 11). Данный массив имеет размерность 2*3 и содержит в первой строке матрицы значения градусов, во второй – значения минут дирекционных углов. В строке 12 одномерный массив distance [3] инициализируется значениями расстояний между отмеченными на карте точками, причем эти расстояния уже переведены в метры. В строке 13 одномерный массив radian[3] для дирекционных углов направлений в радианах, инициализируется нулевыми значениями.

Таким образом, пользователь, работая с программой, не вводит никаких данных, все необходимые исходные данные встроены в код программы. Это сделано в учебно-методических целях, поскольку программа предназначена для анализа листинга с кодом и обучения студентов. Так легче проследить в коде программы изменения величин в ходе работы программы и тем самым ознакомиться с особенностями обработки данных, представленных в массивах.

Обработка данных начинается в строке 15, в которой используется цикл for для перебора всех значений массива дирекционных углов. В цикле выполняется сложение значений градусов с минутами, представленными как дробная часть градусов. В результате в первой строке массива gridAzimuth[0][j] (индекс 0) сохраяются дирекционные углы в градусах с дробной частью. Далее полученные значения преобразуются в радианы. Здесь используется именованная константа Pi (определенная ранее в строке 3) и равная π = 3,141592653589793L. Суффикс L в конце записи числа π используется, чтобы сохранить в константе 16 значащих цифр числа «пи». Такая запись означает, что данная числовая константа имеет тип данных long double в отличие от констант типа double, устанавливаемых по умолчанию.

В обработке двумерных массивов используются вложенные циклы – особые управляющие конструкции, например в строках 21–22 вложенные циклы for используются для вычисления Х и Y координат точек. Конструкция, представленная далее, позволяет перебрать все элементы двумерного массива при вычислении Х и Y координат трех точек.

for(int i = 0; i < 2; i++)

for(int j = 1; j <= 3; j++)

calculatedXYcoordinates[i][j%3] =

calculatedXYcoordinates[i][j-1]+distance[j-1]*cos(i*Pi/2-radian[j-1]);

Обращаем внимание читателя на две особенности рассматриваемой конструкции. Первая заключается в том, что счетчик вложенного цикла начинается со значения j = 1 и заканчивается j = 3. Такой выбор начального и конечного значения позволяет при вычислении выражения j %3 получить следующие значения индекса массива: 1, 2 и 0 (остаток от деления 3 %3 = 0). В результате таких манипуляций с индексом нет необходимости выполнять циклический сдвиг элементов массива, чтобы разместить элементы массива в правильной последовательности. Вторая особенность заключается в выражение cos(i*Pi/2-radian[j]), которое используется в инструкции цикла и позволяет вычислять как косинус, так и синус некоторого угла. В этом выражении счетчик цикла i включен в тело внутреннего цикла for и реализует либо функцию косинуса, либо функцию синуса с помощью одной математической формулы. Действительно, при i = 0, данная запись эквивалентна выражению cos(radian[j]), а при i=1, – выражению sin(radian[j]).

Без манипуляции индексами (вида j %3) массива, (если использовать одинаковые начальные индексы для внешнего и внутреннего циклов), потребуется циклическая перестановка элементов массива.

for(int i = 0; i < 2; i++)

for(int j = 0; j < 3; j++)

calculatedXYcoordinates[i][j] =

calculatedXYcoordinates[i][j]+distance[j]*cos(i*Pi/2-radian[j]);

Циклическую перестановку можно осуществить с помощью следующих инструкций:

double temp;

for(int i = 0; i < 2; i++){

temp = calculatedXYcoordinates[i][2];

for(int j = 2; j > 0; j--)

calculatedXYcoordinates[i][j]=calculatedXYcoordinates[i][j-1];

calculatedXYcoordinates[i][0] = temp; }

В данном фрагменте кода вычисленные значения координат записываются в массив с последовательным перебором индексов, Х и Y координаты точки В – в первый столбец двумерного массива с индексом 0, координаты точки С – во второй столбец с индексом 1 и координаты точки А – в третий столбец с индексом 2. Для расчета разностей измеренных и вычисленных координат в цикле for возможно использовать одинаковые индексы в обозначении измеренных и вычисленных координат, принадлежащих одной точке. В этом случае для осуществления циклического сдвига значений координат в массиве используется временная переменная temp. Далее в строках 24-26 выполняется вычисление разностей координат: из измеренных координат вычитаются вычисленные координаты точек, результаты помещаются в двумерный массив errorXYcoordinates[i][j]. Оставшаяся часть кода (строки 27–42) предназначена для форматированного вывода результатов на экран. Поскольку результаты вычислений координат имеют погрешности более 1 м, Х и Y координаты точек выводятся на экран в виде целых чисел, дробная часть не высвечивается. Для этого в строке 27 поток вывода информации переводится в режим fixed и устанавливается точность вывода чисел до целых метров с помощью объекта setprecision (0). Здесь 0 означает вывод с точностью до целых чисел.

В результате работы программа напечатает следующее:

Рассмотренная программа предназначена для первоначального ознакомления студентов с одномерными и двумерными массивами. Данный пример также демонстрирует использование вложенных циклов for для перебора элементов численного двумерного массива (матрицы). Отметим, что массивы, особенно двумерные, традиционно считаются конструкциями языка программирования, требующими внимательного обращения с ними и скрупулёзного разбора процесса изменения индексов.

Выводы

Разработана учебная программа для студентов картографов и геодезистов, изучающих основы программирования на языке С++. Программа демонстрирует вычисление плоских прямоугольных координат трех точек, заданных на топографической карте. Вычисления координат точек проводятся на основе решения прямой геодезической задачи. Подробно описывается код программы и поясняется назначение использованных инструкций. В программе используются двумерные и одномерные массивы, позволяющие хранить значения координат, дирекционных углов и расстояний. На экран координаты точек и погрешности определения координат выводятся с точностью до целых метров. Разработанная программа иллюстрирует использование массивов для решения прямой геодезической задачи и вычисление плоских прямоугольных координат на основе применения технологии процедурного программирования.

Библиографическая ссылка