В работе исследуется многосвязная система автоматического управления (МСАУ), где одновременно осуществляется регулирование нескольких взаимосвязанных координат и наблюдается явление запаздывания. Далее будем рассматривать однотипную МСАУ – многосвязная система с одинаковыми подсистемами.
Задача управления объектами с запаздыванием довольно непростая. Наличие задержки в контуре управления приводит к возрастанию фазового сдвига, что способна спровоцировать неустойчивость замкнутой системы, а именно при наличии небольших коэффициентах усиления регулятора. Проблема еще больше усугубляется, если объект управления многомерный.
Постановка задачи: рассматривается линейная многосвязная система автоматического управления, состоящая из множества однородных сепаратных подсистем и связей через многомерный объект управления:
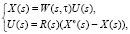(1)
где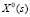 
, X(s), U(s) – векторы задающих, регулируемых, управляющих воздействий соответственно; 
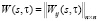– матричная передаточная функция (МПФ) многомерного объекта по управляющим воздействиям, с запаздыванием; 
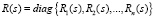– МПФ сепаратных регуляторов.
С целью изучения МСАУ с запаздыванием используется подход, представленный в труде [1], при котором линейная МСАУ описывается на уровне физических подсистем и многомерных элементов связи между ними.
Цель исследования: разработка методов оценки критического значения запаздывания в прямых и перекрестных связях МСАУ с помощью метода декомпозиции, на основе описания системы через характеристики связей и характеристики подсистем [1].
Материалы и методы исследования
Рассмотрим однородную МСАУ с запаздыванием в подсистемах. Поскольку подсистемы однотипные, то их передаточные функции (ПФ) можно представить как
R1W11e-ts = R2W22e-ts = ... = RnWnne-ts = RWe-ts, (2)
а ПФ индивидуальных характеристик подсистем примут вид [1]:
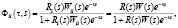
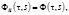
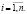(3)
Для полной МСАУ, состоящей из n подсистем и соответствующей системы уравнений (1), характеристика связи (ХС) в общем виде между k подсистемами имеет вид
, 
, 
.
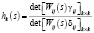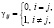
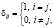
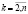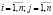Характеристическое уравнение однотипной МСАУ имеет вид
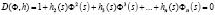. (4)
Перепишем равенство (4) сравнительно разомкнутых подсистем W(t, s) = RWe-ts в общем виде для удобства вычисления критического значения запаздывания tк [2]:
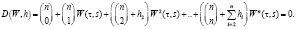(5)
Проанализируем уравнение связей
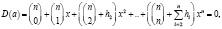(6)
относительно переменной x, что выходит из (5) с помощью подстановки W(t, s) = x, где запаздывание в подсистемах.
Перенеся на комплексную плоскость годограф функции W(jω) c запаздыванием, а также корни характеристического уравнения связи (6)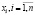 
, можно найти критическое значение запаздывания τiкр [3].
Критическое запаздывание находится в точке пересечения корня уравнения (6)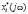 
и годографа подсистемы W(jω). В МСАУ для нахождения критического значения запаздывания tкр необходимо, чтобы годограф W(jω) построенный на одной комплексной плоскости с корнями уравнения (6), проходил через ближайший из них и не охватывал при этом другие корни, то есть МСАУ оказывается на границе устойчивости. Значения ωiср (частота среза) и τiкр определяются из выражения: 
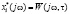. Из этого условия получаем систему из двух уравнений относительно t и ω0 [4]:
|W(t,ω0)| = |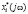
|, arg W(t,ω0) = arg 
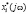. (7)
Минимальным из найденных значений ti является критическое значение запаздывания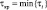 
, 
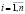[4].
Результаты исследования и их обсуждение
Пример 1. Многосвязная система автоматического управления с запаздыванием в подсистемах.
В качестве примера рассмотрим дву- связную систему. Объектом исследования является многомерный объект с запаздыванием в подсистемах. ПФ разомкнутой подсистемы равна
,
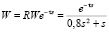характеристика связи h2 = 0,2 [5].
Характеристическое уравнение системы:
.
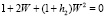Корни уравнения связи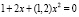 
равны:
x1 = –0,56 + 0,5j; x2 = –0,56 – 0,5j.
C целью расчета значения критического запаздывания используем графоаналитический метод, который эффективен в случае, если нет необходимости в высокой точности решений дифференциальных уравнений низкого порядка. В зависимости от способа построения графиков изменяется достоверность этого метода, которая еще и возрастает при увеличении их масштаба (рис. 1).
Так как годограф с запаздыванием W(jω) пересекает один из корней уравнения связи, следовательно, система на грани устойчивости. С помощью графоаналитического способа найдено критическое значение запаздывания τкр = 0,15 сек.
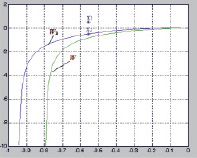
Рис. 1. Годограф МСАУ с критическим значением запаздывания
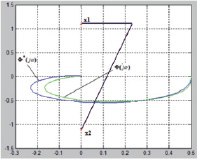
Рис. 2. Годограф МСАУ с запаздыванием в подсистемах, построенный на плоскости корней уравнения связи
Чтобы определить устойчивость МСАУ с запаздыванием в подсистемах, воспользуемся частотным критерием. По характеристическому уравнению (4) получаем уравнение связи
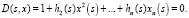(8)
На одной комплексной плоскости строим годограф Ф*(jw,t) (подсистема с запаздыванием) для всех w∈(0, +∞) и корни уравнения связи (8). Согласно критерию устойчивости для многомерных систем необходимо и достаточно, чтобы годограф амплитудно-фазовой характеристики подсистем Ф*(jw,t), для всех w∈(0, +∞), построенный на плоскости корней уравнения связи, не охватывал ни один из его корней (рис. 2). На рис. 2 показана устойчивая МСАУ, где Ф(jw) – годограф без запаздывания.
Многосвязная система автоматического управления с запаздыванием в перекрестных связях
Рассмотрим однородную МСАУ с запаздыванием в перекрестных связях. Для данного вида системы характеристическое уравнение однотипной МСАУ:
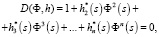
где
, 
,
.
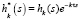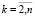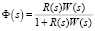Введем переменную Wp, которая обозначает разомкнутую систему, и перепишем относительно нее характеристическое уравнение. Так как Wp = R(s)W(s), следовательно характеристическое уравнение МСАУ примет вид [6]:
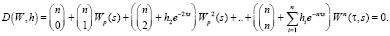(9)
Уравнение связи относительно переменной Wp = x 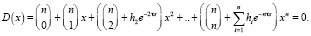(10):
(10)
Решением уравнения связи (10) будут корневые годографы xi(jω) [3, 4].
Пример 2. Рассмотрим МСАУ с двумя подсистемами и запаздыванием в перекрестных связях. ПФ подсистемы равна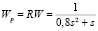 
, характеристика связи 
.
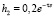Корни уравнения связи (10) при t = 0 в перекрестных связях и w = 0: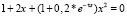 
(10) равны x1 = –0,5611 + 0,5442i; x2 = –0,5509 – 0,4537i.
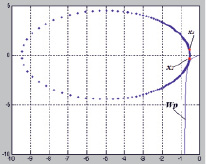
Рис. 3. Годограф МСАУ с запаздыванием в перекрестных связях
При постепенном увеличении значения запаздывания t видим, что корневые годографы xi(jω) не пересекают годографы подсистем. Это означает, что запаздывание не влияет на устойчивость системы (рис. 3). На устойчивость разомкнутой системы можно повлиять, изменив коэффициенты характеристик связей h2.
Как видим, используя метод декомпозиции при построении годографа подсистем и связей, предоставляется возможность применять известные частотные критерии устойчивости и вычислять критические значения запаздывания tкр.
Многосвязная система автоматического управления с запаздыванием одновременно в подсистемах и перекрестных связях
В общем виде характеристическое уравнение МСАУ с однотипными подсистемами и запаздыванием одновременно в подсистемах и перекрестных связях имеет вид
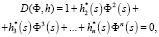
где
, 
,
.
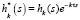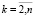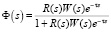Запишем по аналогии характеристическое уравнение МСАУ относительно разомкнутых подcистем:
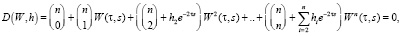(11)
и уравнение связи
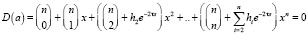. (12)
Далее, если построить на комплексной плоскости годограф разомкнутых подсистем Wр(jω,t) и корневой годограф уравнения связи (12) , то можно найти критическое значение запаздывания τiкр и исследовать систему на устойчивость (рис. 4).
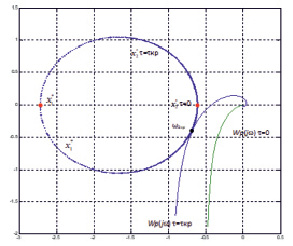
Рис. 4. Годограф МСАУ с запаздыванием в прямых и перекрестных связях
Значения τiкр определяются из выражения
y1 = φо(ω) – ω1срτiкр, τiкр = (φо(ω) – y1)/ω1ср,
где y1 – argx1, φо(ω1ср) – argWp(jw) на частоте ωiср = 1.
Минимальным из найденных значений ti – критическое значение запаздывания τкр = min{τiкр}, i = 1,n. В примере 2 критическое значение запаздывания равно τкр = 0,087 сек.
Заключение
В ходе выполненной работы применен способ оценки критического значения запаздывания в прямых и перекрестных связях МСАУ с помощью метода декомпозиции.
С помощью известного критерия устойчивости для МСАУ рассмотрена ее устойчивость с запаздыванием в подсистеме, перекрестных связях. Также рассмотрен алгоритм определения критического значения запаздывания для МСАУ по разомкнутым и замкнутым подсистемам. Проверена эффективность разработанной методики нахождения критического значения запаздывания tкр. Результаты и проверка системы на устойчивость подтверждены моделированием МСАУ по результатам переходных процессов.
Работа выполнена при поддержке Российского фонда фундаментальных исследований (Гранты РФФИ № 18-08-00702 А, 18-08-01299 А).
Библиографическая ссылка
Ильясов Б.Г., Саитова Г.А., Елизарова А.В. ИССЛЕДОВАНИЕ МНОГОСВЯЗНОЙ СИСТЕМЫ УПРАВЛЕНИЯ С ЗАПАЗДЫВАНИЕМ МЕТОДОМ ДЕКОМПОЗИЦИИ // Современные наукоемкие технологии. – 2019. – № 3-2. – С. 177-181;URL: https://top-technologies.ru/ru/article/view?id=37461 (дата обращения: 21.11.2024).