Деятельность любого предприятия всегда необходимо оценивать, то есть оценивать показатели качества производства и эксплуатации. В предыдущих работах [1, 2] показана важность рассмотрения показателей качества элементов кранового оборудования металлургических предприятий – конструкций мостовых кранов как сложной технической системы. Международный стандарт ГОСТ Р ИСО 9000-2015 [3] предусматривает тщательную разработку измеримых показателей деятельности для облегчения проведения мониторинга оценки деятельности. Согласно ГОСТ Р ИСО 9000-2015 лишь тщательно продуманные показатели облегчают проведение мониторинга и оценки деятельности. Качество объединяет большое множество характеристик и показателей. Поэтому с целью определения наиболее значимых показателей целесообразно произвести снижение размерности пространства разнородных данных.
Таким образом, снижение размерности данных в задачах оценки качества сложных технических систем металлургических предприятий представляет собой актуальную и важную проблему.
Выделение показателей качества, значения которых оказывают существенное влияние на производственную и эксплуатационную деятельность, очень важно в дальнейшем для принятия управленческих решений.
Целью данной статьи является количественное модельное снижение размерности показателей качества элементов конструкции металлургических мостовых кранов.
Материалы и методы исследования
Различают большое количество многомерных методов снижения размерности: компонентный анализ, метод опорных векторов, метод неотрицательной матричной факторизации, метод нелинейного снижения размерности и визуализации многомерных данных t-SNE [4–6]. Однако практически все методы за исключением компонентного анализа требуют больших трудоемких вычислительных затрат. В наиболее выгодном положении здесь оказывается метод главных компонент, потому что имеется дополнительная информация о состоянии рассматриваемых конструкций кранов. В методе главных компонент линейные комбинации случайных величин определяются характеристическими векторами ковариационной матрицы. Главные компоненты представляют собой ортогональную систему координат, в которой дисперсии компонент характеризуют их статистические свойства.
На основе [1, 2, 7, 8] выделим 15 показателей конструкции металлургического мостового крана, известных в процессе эксплуатации металлургического предприятия на протяжении 15 лет, и представим в табл. 1.
Таблица 1
Показатели качества эксплуатации конструкции
|
Показатели качества эксплуатации конструкции |
||
|
Надежность |
1 |
Количество конструкций, шт |
|
2 |
Число наработанных циклов, циклы |
|
|
3 |
Наработка без вынужденных перерывов, % |
|
|
4 |
Уровень ремонтопригодности, % |
|
|
5 |
Показатели надежности, % |
|
|
6 |
Выполнение руководств эксплуатации, % |
|
|
7 |
Экономические показатели, % |
|
|
Безопасность |
8 |
Аварийные события, к-во |
|
9 |
Тяжелонагруженные режимы работы, % |
|
|
10 |
Нарушения стандартов качества эксплуатации, % |
|
|
11 |
Нарушения требований руководств эксплуатации, % |
|
|
12 |
Нарушения технического обслуживания, % |
|
|
13 |
Социальные и индустриальные риски, к-во |
|
|
14 |
Экологические риски, к-во |
|
|
15 |
Техногенные риски, к-во |
|
В показателях надежности учитываются и экономические. Реализуем метод главных компонент [6].
В табл. 2 представлены показатели процессов по годам (г) эксплуатации и их нормированные данные.
Таблица 2
Нормирование показателей эксплуатации конструкции
|
Показатели |
г |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
|
1 |
15 |
18000 |
95 |
90 |
95 |
100 |
100 |
0 |
100 |
1 |
15 |
10 |
0 |
0 |
0 |
|
|
2 |
15 |
19000 |
95 |
90 |
90 |
100 |
99 |
0 |
100 |
1 |
14 |
2 |
0 |
0 |
0 |
|
|
3 |
15 |
20000 |
95 |
85 |
95 |
95 |
99 |
0 |
100 |
1 |
13 |
2 |
0 |
0 |
0 |
|
|
4 |
15 |
17000 |
90 |
85 |
95 |
95 |
100 |
1 |
100 |
5 |
12 |
3 |
1 |
1 |
1 |
|
|
5 |
14 |
16000 |
90 |
85 |
95 |
95 |
99 |
2 |
100 |
6 |
11 |
5 |
2 |
1 |
1 |
|
|
6 |
14 |
18000 |
90 |
70 |
90 |
90 |
100 |
5 |
100 |
7 |
10 |
11 |
5 |
4 |
4 |
|
|
7 |
15 |
18000 |
85 |
75 |
90 |
90 |
100 |
1 |
90 |
8 |
2 |
12 |
1 |
1 |
1 |
|
|
8 |
13 |
19000 |
85 |
80 |
95 |
90 |
100 |
0 |
90 |
2 |
3 |
5 |
0 |
0 |
0 |
|
|
9 |
13 |
20000 |
85 |
85 |
95 |
100 |
90 |
0 |
95 |
1 |
5 |
5 |
0 |
0 |
0 |
|
|
10 |
13 |
18000 |
80 |
75 |
85 |
95 |
80 |
3 |
95 |
1 |
5 |
5 |
3 |
1 |
2 |
|
|
11 |
14 |
18000 |
80 |
80 |
85 |
85 |
85 |
4 |
95 |
1 |
4 |
3 |
4 |
4 |
4 |
|
|
12 |
12 |
18000 |
80 |
80 |
85 |
80 |
80 |
2 |
95 |
5 |
3 |
2 |
2 |
1 |
0 |
|
|
13 |
15 |
18000 |
70 |
70 |
85 |
95 |
80 |
1 |
90 |
3 |
2 |
2 |
1 |
1 |
1 |
|
|
14 |
14 |
18000 |
70 |
60 |
80 |
95 |
80 |
0 |
90 |
1 |
1 |
1 |
0 |
0 |
0 |
|
|
15 |
14 |
18000 |
65 |
60 |
80 |
95 |
85 |
1 |
95 |
2 |
2 |
2 |
1 |
1 |
1 |
|
|
X |
14 |
18200 |
83,667 |
78 |
89,333 |
93,333 |
91,8 |
1 |
95,667 |
3 |
6,8 |
4,667 |
1 |
1 |
1 |
|
|
S |
0,747 |
693,333 |
7,600 |
7,733 |
4,800 |
4,222 |
8,347 |
1,244 |
3,467 |
2,133 |
4,560 |
2,711 |
1,244 |
0,800 |
0,933 |
|
|
Нормированные показатели |
1 |
1,250 |
–0,288 |
1,491 |
1,552 |
1,181 |
1,579 |
0,982 |
–1,071 |
1,250 |
–0,938 |
1,798 |
1,967 |
–1,071 |
–1,250 |
–1,071 |
|
2 |
1,250 |
1,154 |
1,491 |
1,552 |
0,139 |
1,579 |
0,863 |
–1,071 |
1,250 |
–0,938 |
1,579 |
–0,984 |
–1,071 |
–1,250 |
–1,071 |
|
|
3 |
1,250 |
2,596 |
1,491 |
0,905 |
1,181 |
0,395 |
0,863 |
–1,071 |
1,250 |
–0,938 |
1,360 |
–0,984 |
–1,071 |
–1,250 |
–1,071 |
|
|
4 |
1,250 |
–1,731 |
0,833 |
0,905 |
1,181 |
0,395 |
0,982 |
–0,268 |
1,250 |
0,938 |
1,140 |
–0,615 |
–0,268 |
0,000 |
0,000 |
|
|
5 |
–0,089 |
–3,173 |
0,833 |
0,905 |
1,181 |
0,395 |
0,863 |
0,536 |
1,250 |
1,406 |
0,921 |
0,123 |
0,536 |
0,000 |
0,000 |
|
|
6 |
–0,089 |
–0,288 |
0,833 |
–1,034 |
0,139 |
–0,789 |
0,982 |
2,946 |
1,250 |
1,875 |
0,702 |
2,336 |
2,946 |
3,750 |
3,214 |
|
|
7 |
1,250 |
–0,288 |
0,175 |
–0,388 |
0,139 |
–0,789 |
0,982 |
–0,268 |
–1,635 |
2,344 |
–1,053 |
2,705 |
–0,268 |
0,000 |
0,000 |
|
|
8 |
–1,429 |
1,154 |
0,175 |
0,259 |
1,181 |
–0,789 |
0,982 |
–1,071 |
–1,635 |
–0,469 |
–0,833 |
0,123 |
–1,071 |
–1,250 |
–1,071 |
|
|
9 |
–1,429 |
2,596 |
0,175 |
0,905 |
1,181 |
1,579 |
–0,216 |
–1,071 |
–0,192 |
–0,938 |
–0,395 |
0,123 |
–1,071 |
–1,250 |
–1,071 |
|
|
10 |
–1,429 |
–0,288 |
–0,482 |
–0,388 |
–0,903 |
0,395 |
–1,414 |
1,339 |
–0,192 |
–0,938 |
–0,395 |
0,123 |
1,339 |
0,000 |
1,071 |
|
|
11 |
–0,089 |
–0,288 |
–0,482 |
0,259 |
–0,903 |
–1,974 |
–0,815 |
2,143 |
–0,192 |
–0,938 |
–0,614 |
–0,615 |
2,143 |
3,750 |
3,214 |
|
|
12 |
–2,768 |
–0,288 |
–0,482 |
0,259 |
–0,903 |
–3,158 |
–1,414 |
0,536 |
–0,192 |
0,938 |
–0,833 |
–0,984 |
0,536 |
0,000 |
–1,071 |
|
|
13 |
1,250 |
–0,288 |
–1,798 |
–1,034 |
–0,903 |
0,395 |
–1,414 |
–0,268 |
–1,635 |
0,000 |
–1,053 |
–0,984 |
–0,268 |
0,000 |
0,000 |
|
|
14 |
–0,089 |
–0,288 |
–1,798 |
–2,328 |
–1,944 |
0,395 |
–1,414 |
–1,071 |
–1,635 |
–0,938 |
–1,272 |
–1,352 |
–1,071 |
–1,250 |
–1,071 |
|
|
15 |
–0,089 |
–0,288 |
–2,456 |
–2,328 |
–1,944 |
0,395 |
–0,815 |
–0,268 |
–0,192 |
–0,469 |
–1,053 |
–0,984 |
–0,268 |
0,000 |
0,000 |
Нормирование показателей необходимо для последующей обработки данных.
С целью получения нормированных данных по каждому показателю вычислено среднее значение (X), среднее квадратическое отклонение S (стандартное отклонение) (1).
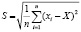, (1)
где X – среднее значение.
С помощью полученных данных произведено нормирование переменных по формуле 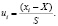(2).
(2)
Далее построена матрица корреляции 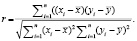(3).
(3)
Во всех случаях воспользуемся стандартными функциями MS-Excel и его надстройкой «Анализ данных».
Затем были найдены собственные значения λ и собственные векторы следующего вида (4).
(4)
Матрица в табл. 3 обозначена как исходная (5) и сформирована симметричная матрица с отрицательными значениями λ (6).
Таблица 3
Матрица корреляции
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
|
|
1 |
1 |
–0,088 |
0,283 |
0,132 |
0,207 |
0,490 |
0,462 |
–0,249 |
0,256 |
0,059 |
0,473 |
0,153 |
–0,249 |
–0,057 |
0 |
|
2 |
–0,088 |
1 |
0,140 |
0,154 |
0,150 |
0,190 |
0,028 |
–0,399 |
0,118 |
–0,534 |
–0,019 |
–0,119 |
–0,399 |
–0,323 |
–0,31 |
|
3 |
0,283 |
0,140 |
1 |
0,847 |
0,847 |
0,224 |
0,817 |
–0,063 |
0,698 |
0,134 |
0,853 |
0,407 |
–0,063 |
–0,086 |
–0,082 |
|
4 |
0,132 |
0,154 |
0,847 |
1 |
0,8 |
0,201 |
0,563 |
–0,211 |
0,571 |
–0,089 |
0,712 |
0,125 |
–0,211 |
–0,227 |
–0,246 |
|
5 |
0,207 |
0,150 |
0,847 |
0,800 |
1 |
0,304 |
0,818 |
–0,253 |
0,477 |
0,152 |
0,66 |
0,38 |
–0,253 |
–0,242 |
–0,233 |
|
6 |
0,490 |
0,190 |
0,224 |
0,201 |
0,304 |
1 |
0,27 |
–0,539 |
0,282 |
–0,41 |
0,457 |
0,006 |
–0,539 |
–0,539 |
–0,377 |
|
7 |
0,462 |
0,028 |
0,817 |
0,563 |
0,818 |
0,270 |
1 |
–0,164 |
0,506 |
0,334 |
0,685 |
0,533 |
–0,164 |
–0,078 |
–0,075 |
|
8 |
–0,249 |
–0,399 |
–0,063 |
–0,211 |
–0,253 |
–0,539 |
–0,164 |
1 |
0,18 |
0,395 |
–0,08 |
0,274 |
1 |
0,927 |
0,924 |
|
9 |
0,256 |
–0,118 |
0,698 |
0,571 |
0,477 |
0,282 |
0,506 |
0,180 |
1 |
0,034 |
0,904 |
0,088 |
0,18 |
0,131 |
0,126 |
|
10 |
0,059 |
–0,534 |
0,134 |
–0,089 |
0,152 |
–0,410 |
0,334 |
0,395 |
0,034 |
1 |
–0,034 |
0,528 |
0,395 |
0,37 |
0,272 |
|
11 |
0,473 |
–0,019 |
0,853 |
0,712 |
0,660 |
0,457 |
0,685 |
–0,080 |
0,904 |
–0,034 |
1 |
0,178 |
–0,08 |
–0,097 |
–0,073 |
|
12 |
0,153 |
–0,119 |
0,407 |
0,125 |
0,380 |
0,006 |
0,533 |
0,274 |
0,088 |
0,528 |
0,178 |
1 |
0,274 |
0,261 |
0,295 |
|
13 |
–0,249 |
–0,399 |
–0,063 |
–0,211 |
–0,253 |
–0,539 |
–0,164 |
1,000 |
0,180 |
0,395 |
–0,080 |
0,274 |
1 |
0,927 |
0,924 |
|
14 |
–0,057 |
–0,323 |
–0,086 |
–0,227 |
–0,242 |
–0,539 |
–0,078 |
0,927 |
0,131 |
0,370 |
–0,097 |
0,261 |
0,927 |
1 |
0,961 |
|
15 |
0,000 |
–0,310 |
–0,082 |
–0,246 |
–0,233 |
–0,377 |
–0,075 |
0,924 |
0,126 |
0,272 |
–0,073 |
0,295 |
0,924 |
0,961 |
1 |
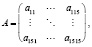(5)
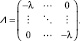(6)
Через определитель (детерминант) суммы матриц ? и А получено выражение (7), правая часть которого является характеристическим уравнением (8), решение которого необходимо для нахождения собственных значений матрицы.
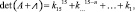(7)
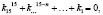(8)
где k – коэффициент, полученный при нахождении определителя.
Корни уравнения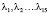 
есть собственные значения матрицы.
После этого для каждого собственного значения (15 значений) построена матрица 9 для последующего нахождения собственных векторов матрицы.
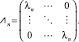(9)
Результаты исследования и их обсуждение
Алгоритм метода главных компонент иллюстрируют табл. 2 и 3.
Затем произведено сложение исходной матрицы (5) с матрицей (9).
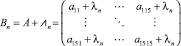(10)
и умножение матрицы (9) на искомый собственный вектор:
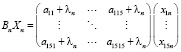. (11)
Полученная матрица представлена в виде системы уравнений 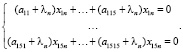(12)
(12)
Выражены корни уравнений через общий множитель c 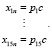(13).
(13)
Далее записаны корни системы уравнений в виде вектора 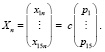(14)
(14)
Где p определяются при операции (10), а c – выбран произвольным положительным минимальным значением, и Xn собственный вектор.
Все вычисления были выполнены в пакете Maple 17: были найдены собственные значения λ и собственные векторы, удовлетворяющие соотношению (4).
Из 15 столбцов (значений λ) выбраны два значения λ, берущие на себя всю информационную нагрузку (два максимальных значения λ).
На основе табл. 4 построен график (рисунок): собственный вектор, соответствующий собственному значению 4,362 (синяя линяя); собственный вектор, соответствующий по величине собственному значению 5,458 (красная линия).
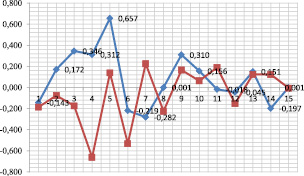
График показателей качества эксплуатации конструкции
Таблица 4
Таблица максимальных собственных значений и собственных векторов
|
Lambda |
|||
|
4,362 |
5,458 |
||
|
Показатели |
1 |
–0,143 |
–0,186 |
|
2 |
0,172 |
–0,076 |
|
|
3 |
0,346 |
–0,173 |
|
|
4 |
0,312 |
–0,662 |
|
|
5 |
0,657 |
0,139 |
|
|
6 |
–0,219 |
–0,533 |
|
|
7 |
–0,282 |
0,225 |
|
|
8 |
0,001 |
–0,225 |
|
|
9 |
0,310 |
0,165 |
|
|
10 |
0,156 |
0,064 |
|
|
11 |
–0,018 |
0,190 |
|
|
12 |
–0,045 |
–0,153 |
|
|
13 |
0,151 |
0,125 |
|
|
14 |
–0,197 |
0,123 |
|
|
15 |
0,001 |
–0,006 |
|
В соответствии с полученным графиком производится отбор показателей, оказывающих наибольшее влияние на качество конструкции.
Максимальные значения в области качества приняли значения «Показатели надежности» (5). Под показателями надежности понимаем безотказность, ремонтопригодность, долговечность. Кроме этого, максимальные значения векторов наблюдаем у показателей безопасности (9) и экономических показателей (7).
Исходя из этого, можно сделать вывод о том, что наибольшее влияние на качество элементов кранового оборудования металлургического предприятия оказывают показатели надежности, безопасности и экономические показатели.
Минимальные значения в области качества имеют показатели, связанные с количеством конструкций (1). Но это говорит лишь о том, что оценка качества каждой конструкции стандартизирована.
После анализа была проверена точность результатов анализа, с помощью формулы (15).
Удельный вклад i-й главной компоненты =
= 
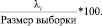(15)
Удельный вклад первой главной компоненты равен 29,1 %, удельный вклад второй главной компоненты равен 36,4 %. Суммарные вклады по двум главным компонентам равны 65,5 %.
Таким образом, доля дисперсии первых двух компонент составляет 65,5 % (из 15 компонент). Следовательно, данные из первых двух компонент могут быть использованы как определяющие, потому что вклад других принимается несущественным, так как составляет менее 40 %. В этом случае анализ методом главных компонент можно считать удовлетворительным.
К наиболее значимым показателям надежности отнесем вероятность безотказной работы конструкции, уровень ее ремонтопригодности и долговечности, а показателям безопасности – режимы работы металлургических мостовых кранов, а также риски, связанные с их эксплуатацией.
Выводы
Оценка качества сложных технических систем представляет собой трудную задачу, потому что это понятие включает большое количество характеристик и показателей. Возникает необходимость выделения основных показателей качества рассматриваемых конструкций.
На сегодняшний день представляется эффективным многомерный метод снижения размерности данных – метод главных компонент.
Применение метода главных компонент структурирует показатели посредством сведения множества переменных к меньшему числу переменных, которые объясняют большую часть вариации в значениях исследуемых данных.
В данном исследовании из 15 показателей (7 показателей надежности и 8 показателей безопасности) были выявлены наиболее значимые 9 показателей, которые оказывают существенное влияние на качество эксплуатации элементов кранового оборудования:
показатели надежности (5 показателей):
– число наработанных циклов (2);
– наработка без вынужденных перерывов (3);
– уровень ремонтопригодности (4);
– показатели надежности (5);
– экономические показатели;
и показатели безопасности (4 показателя):
– тяжелонагруженные режимы работы (9);
– нарушения стандартов качества эксплуатации (10);
– нарушения требований руководств эксплуатации (11);
– социальные и индустриальные риски (13).
Библиографическая ссылка
Извеков Ю.А., Гугина Е.М., Анисимов А.Л., Шеметова В.В. СНИЖЕНИЕ РАЗМЕРНОСТИ В ЗАДАЧАХ ОЦЕНКИ КАЧЕСТВА МОСТОВЫХ КРАНОВ МЕТАЛЛУРГИЧЕСКОГО ПРЕДПРИЯТИЯ // Современные наукоемкие технологии. – 2019. – № 3-2. – С. 171-176;URL: https://top-technologies.ru/ru/article/view?id=37460 (дата обращения: 03.12.2024).