Лесозаготовительными компаниями на транспортно-переместительных операциях используется целый спектр лесовозных автопоездов, оснащенных различными видами трансмиссии: механическими, электрическими, гидромеханическими, гидрообъемными и т.д. В тяжелых условиях работы на вывозке леса, когда автопоезда эксплуатируются не только на дорогах общего пользования и лесовозных дорогах постоянного действия, но и на временных дорогах (усах), а также в сложных условиях эксплуатации, например, на транспортных работах при строительстве линий электропередач, трубопроводов и др., применение автопоездов с гидромеханической трансмиссией предпочтительнее [1, 2].
Ранее в России были разработаны опытные образцы автомобилей с гидромеханической трансмиссией типа НАМИ-076, а также на базе МАЗ-509А и ЗИЛ-131 [3]. В настоящее время Минским заводом колёсных тягачей (фирма VOLAT) выпускается автопоезд-плетевоз МЗКТ-741316+90011 (тягач МЗКТ-741310), оснащенный гидромеханической трансмиссией [4, 5].
Цель исследования: разработать алгоритм и методику расчета для определения скорости и времени движения лесовозных автопоездов на базе автомобилей с гидромеханической трансмиссией.
Материалы и методы исследования
Для определения показателей движения автомобилей (автопоездов) [6–8] с механической трансмиссией получены расчётные зависимости при условии аппроксимации кривой тяговой характеристики в рабочем диапазоне оборотов двигателя семейством кривых вида а – bυ2, (1)количество которых равно числу передач [9, 10].
С использованием этих зависимостей разработаны алгоритмы и программы расчёта показателей движения лесовозных автопоездов [9, 10], которые использовались для решения различных технико-экономических задач на транспорте леса (в частности, для определения оптимальных маршрутов вывозки леса, а также в учебном процессе) и в системах автоматизированного проектирования лесовозных дорог с учётом транспортной составляющей. Проведенными исследованиями доказано, что новые методы тяговых расчётов обеспечивают более высокую точность и адекватность расчётов.
Анализ показал, что зависимость изменения тягового усилия от скорости движения у автомобилей (автопоездов) с гидромеханической трансмиссией принципиально отличается от той же зависимости для автомобилей (автопоездов) с механической трансмиссией. Аппроксимация тяговой характеристики автомобиля с гидромеханической трансмиссией зависимостью (1) приводит к значительным погрешностям.
Достаточная точность определения тягового усилия в зависимости от скорости движения достигается при аппроксимации его по формулам
FT = a + С/υ, (2)
FT = a + С/υ2, (3)
трёхчленным полиномом
FT = a + bυ + сυ2 (4)
и двухчленным полиномом вида
FT = a – bυ1/2. (5)
В зависимостях (2–5) a, b, с – эмпирические коэффициенты.
Результаты исследования и их обсуждение
Для примера в табл. 1 приведены значения тягового усилия в диапазоне допустимых скоростей для третьей передачи КПП для автопоезда на базе МАЗ-509Г при аппроксимации тягового усилия зависимостями (2) и (4). Среднее квадратичное отклонение не превышает 0,3 %, что обеспечивает достаточную точность для практических расчётов.
Таблица 1
Аппроксимация кривой тяговой характеристики автопоезда на базе МАЗ-509 Г
|
υ, м/c |
FT при аппроксимации тягового усилия зависимостью FT = a + b/υ |
FT при аппроксимации тягового усилия зависимостью FT = a + bυ + сυ2 |
|
6,8 |
1041 |
1037 |
|
7,7 |
981,7 |
987,7 |
|
8,8 |
935,3 |
935,9 |
|
9,8 |
898,7 |
897,3 |
|
10,8 |
868,8 |
866,4 |
|
11,8 |
844,0 |
843,4 |
|
12,55 |
829,5 |
831,3 |
В работах [9, 10] путём решения дифференциального уравнения движения получены расчётные зависимости для определения показателей движения автомобилей (автопоездов) с гидромеханической трансмиссией на прямолинейном в профиле участке при условии аппроксимации тягового усилия на каждой передаче зависимостями (2) и (3).
В случае использования для аппроксимации кривой тяговой характеристики гиперболы первой степени дифференциальные уравнения движения имеют следующий вид:
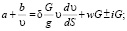(6)
или
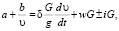(7)
где υ – скорость автопоезда, м/с; δ – коэффициент учета инерции вращающихся масс; S – пройденное расстояние, м; w – коэффициент сопротивления движению; i – уклон.
В случае использования для аппроксимации кривой тяговой характеристики гиперболы второй степени дифференциальные уравнения движения имеют вид
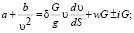(8)
или
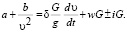(9)
При аппроксимации тягового усилия полиномом второй степени дифференциальное уравнение движения:
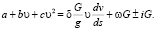(10)
В приведенных зависимостях δ – коэффициент учёта инерции вращающихся масс; ω – основное сопротивление движению (сопротивление качению); i – продольный уклон; G – вес автопоезда, кгс; υ – скорость движения, м/c; s – пройденный путь, м.
В табл. 2 в качестве примера приведены коэффициенты зависимостей, аппроксимирующих тяговую характеристику в виде FT = a + b/υ, коэффициенты учёта инерции вращающихся масс и допустимые по техническим характеристикам автопоезда скорости движения на передачах
Таблица 2
Данные для расчета показателей движения автопоезда на базе МАЗ-509Г+ГКБ8493-10
|
Показатели |
I пер. |
II пер. |
III пер. |
IV пер. |
|
a |
863,83 |
757,143 |
576,0 |
12 |
|
b |
5170,212 |
4039,285 |
3161,2 |
5902,35 |
|
υmin |
1,25 |
3,5 |
6,8 |
11,55 |
|
υmax |
4,5 |
7,8 |
12,55 |
16,85 |
|
δГ |
1,7 |
1,25 |
1,048 |
1,032 |
|
δП |
2,7 |
1,61 |
1,11 |
1,08 |
Чтобы упростить расчетные зависимости, обозначим в формулах (6 )и (7):
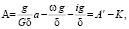(11)
где
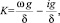
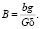(12)
В случае аппроксимации тяговой характеристики на каждой передаче зависимостью A + b/υ решение уравнения получается в следующем виде:
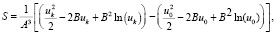(13)
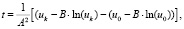(14)
где uk = Aυk + B, u0 = Aυ0 + B.
При аппроксимации гиперболой второй степени:
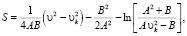(15)
При А < 0: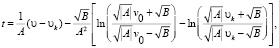 
(16)
При А > 0: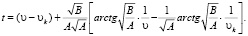 
(17)
Время разгона и замедления определяется по формуле (16), если А < 0, по формуле (17), если А > 0. Полученные уравнения дают возможность определить показатели неустановившегося движения автомобиля (автопоезда) на прямолинейных в профиле участках дороги.
С использованием зависимостей (13) и (14) можно аналитическим методом решать основные задачи тяговых расчетов. Обозначив
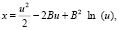(18)
у = и – В? ln(u) (19)
получим
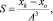(20)
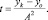(21)
Решение основных четырех задач тяговых расчетов производится следующим образом:
1. Определение расстояния S, пройденного при разгоне или замедлении от начальной скорости υ0 до конечной υк.
Здесь
u0 =(Aυ0 + B) (22)
и
uk = (Aυk + B), (23)
x0 = f(u0) и xk = f(uk),
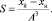
2. Расчет скорости υк в конце участка длиной S при заданной начальной скорости движения. Для заданного уклона определяется величина u0 = (Aυ0 + B); по формуле рассчитывается x0 = f(u0). Вычисляется величина
xk = f(uk) = x0 ± SA3. (24)
При различных значениях υк определяется u = (Aυk + B)и xk = f(u) по формуле (18). Сравнивается значение xk, определенное по формуле (18) и по формуле (24). Для заданной точности расчетов при необходимости производится интерполяция. За искомое значение υk принимается значение, при котором выполняется условие равенства хk, определенных по формуле (18) и (24).
3. Определение времени движения на участке при изменении скорости движения от υ0 до υк. Так же как и при решении второй задачи, определяется uk0 и uк. Определяются y0 = f(u0) и yk = f(uk), а также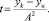 
4. Определение скорости движения, которой достигнет автопоезд за время t при заданной начальной скорости движения υ0. Вычисляется величина u0 = (Aυ0 + B) и y0 = f(u0). Определяется
yk = (tA2 + y0). (25)
При различных значениях υk определяется uk = (Aυk + B), затем сравниваются значения yk, определенные по формуле (25) и формуле (19). Для достижения достаточной точности расчета при необходимости производится интерполяция. За искомое значение υk принимается значение, при котором выполняется условие равенства yk, определенных по формулам (21) и (25).
С использованием зависимостей (20) и (21) достаточно просто определяется расстояние, пройденное автомобилем (автопоездом) с гидромеханической трансмиссией при изменении скорости от υ0 до υк и время движения на участке при изменении скорости в тех же пределах.
Определение же скорости υk, которой автомобиль (автопоезд) с гидромеханической трансмиссией достигнет на определённом расстоянии s, υк или за определенный промежуток времени t, затруднительно, так как для получения достаточно точных результатов требуется производить большой объём итеративных вычислений.
Кроме того, приведенные зависимости могут использоваться лишь при определении показателей движения на прямолинейных в профиле участках дороги. Для определения показателей движения на участках вертикальных кривых на основе решения дифференциального уравнения движения выведены зависимости, обеспечивающие достаточную точность расчетов при поэтапном решении.
Дифференциальное уравнение движения (26) можно представить в следующем виде:
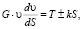(26)
где Т – среднее или среднеинтегральное значение тягового усилия в заданном диапазоне скоростей υ0 – υк, кгс;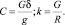 
Среднее значение Т в заданном диапазоне при аппроксимации тягового усилия зависимости F = a + b/υ определяется как средняя величина от значений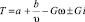 
в начале, середине и в конце диапазона υ0 – υк. Среднее интегральное значение определяется по формуле
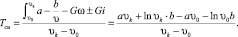(27)
После интегрирования дифференциального уравнения движения (26) получаем зависимости для определения расстояния пройденного автопоездом при изменении скорости движения в диапазоне скоростей υ0 – υк и υк при движении с начальной скоростью υ0 на расстоянии S.
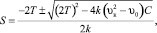(28)
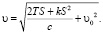(29)
Для определения времени движения решается дифференциальное уравнение движения на участках вертикальных кривых в виде
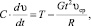(30)
где υср – среднее значение скорости движения в диапазоне υ0 – υк.
Решая уравнение (30), получаем формулу для определения времени движения
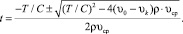(31)
Для расчетов и построения графика скоростей движения вычисленный диапазон скоростей движения на третьей передаче разбивается на интервалы в 1 м/c, для которых рассчитываются суммарные значения уклонов (i) и основного сопротивления движению, величины пройденного расстояния ?S и время движения в заданных интервалах скоростей и суммарные расстояния и время движения. Результаты расчетов сведены в табл. 3.
Таблица 3
Показатели движения автопоезда
|
Диапазон скоростей, м/c |
υр, м/с |
T |
?S, м |
S, м |
i0 + ω |
ik + ω |
?t, сек |
t, сек |
|
7–8 |
8 |
998,75 |
22,08 |
22,08 |
–0,00 |
–0,80552 |
2,96 |
2,96 |
|
8–9 |
9 |
1113,88 |
22,71 |
44,79 |
–0,00552 |
–0,0112 |
2,674 |
5,634 |
|
9–10 |
10 |
1145,39 |
22,35 |
67,65 |
–0,0112 |
–0,01639 |
2,387 |
8,021 |
|
10–11 |
11 |
1349,13 |
23,41 |
91,06 |
–0,01639 |
–0,0227 |
2,23 |
10,251 |
|
11–11,38 |
11,48 |
1544,38 |
8,94 |
100 |
0,0227 |
0,8225 |
0,799 |
11,15 |
При определении показателей движения поэтапно (через заданные интервалы скорости) и сразу на всем заданном участке расхождения, суммарная погрешность не превышает 0,6 %. То есть обеспечивается точность расчетов, достаточная для практических целей. Поэтому поэтапные расчеты целесообразно производить лишь при необходимости построения детального графика скоростей, времени и режимов движения.
Расчет скорости и времени движения по данной схеме с использованием приведенных зависимостей не встречает затруднений, если в начальной точке выпуклой кривой Т > 0, а в начальной точке вогнутой кривой T < 0, при выполнении этого условия в первом случае увеличение скорости движения, а во втором – снижение скорости будет происходить на всем протяжении вертикальной кривой.
При невыполнении этих условий на определенном расстоянии от начала расчетов вектор изменения скорости движения будет меняться на противоположный (на вертикальной выпуклой кривой υ, снизившись до min значения в определенной точке, при дальнейшем движении будет возрастать, а на вертикальной вогнутой, достигнув max значения, будет снижаться).
В точке экстремума первая производная dυ/dS.
Следовательно
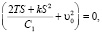
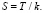(32)
Пример. Определить расстояние до точки экстремума скорости и экстремальное значение скорости при движении автопоезда на базе МАЗ-509Г с полной нагрузкой (G = 30000 кгс) на третьей передаче по вертикальной кривой радиусом – 2500, с начальной скоростью 8 м/c; а = 576, b = 3181,2, i = –0,02, w = 0,02, c = 3204;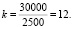 
Так как на первом этапе расчетов конечное значение скорости υ не задано, то определяем ориентировочное значение с использованием значения υ2.
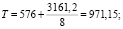
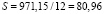м;
м/с.
На втором этапе расчетов определяются уточненные значения T, υ и S.
Среднеинтегральное значение T рассчитано по формуле (27) = 939,9.
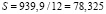м; 
м/с.
Для оценки точности расчетов определим S и υ с использованием результатов второго этапа расчетов: T = 941,63; S = 941,62/17 = 78,47 м; ? = 0,18.
м/с.
Расхождение по расстоянию до точки экстремума составляет 0,19 %, по скорости в точке экстремума 0,05 %. Следовательно, для получения достаточно точных для практических целей результатов достаточно проводить расчеты в 2 этапа.
При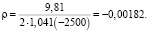 
Время движения на участке:
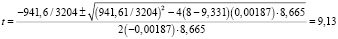с.
Таблица 4
Определение расстояния до точки экстремума скорости
|
Диапазон скоростей, м/с |
Т, кгс |
i0 + ω |
i0 + ω |
S0, м |
Sк, м |
Sэ, м |
|
8–8,5 |
959,7 |
0,000 |
0,00609 |
0 |
15,22 |
79,97 |
|
8,5–9 |
770,4 |
0,0609 |
0,0144 |
15,22 |
37,16 |
64,2 |
|
9–9,5 |
482,1 |
0,0144 |
– |
– |
– |
– |
|
9–9,34 |
492,1 |
– |
– |
37,16 |
78,17 |
41,01 |
Таким образом, при наличии в рассматриваемом диапазоне расстояний и скорости движения точки экстремума скорости следует по формуле (31) и (29) определить расстояние до точки экстремума и экстремальное значение скорости движения, а затем время движения по формуле (31). При необходимости построения детального графика скорости движения автопоезда скорость и время движения определяются поэтапно в промежуточных точках по схеме, приведенной при формировании табл. 4.
При поэтапном расчете, через небольшие интервалы скоростей можно получить более полные результаты. Поделив диапазон скоростей с интервалом 0,5 м/с, определяем по формуле (27) значения T, соответствующие им значения i. Затем по формуле (28) определяется расстояние, которое пройдет автопоезд до достижения максимальной скорости в заданном интервале и по формуле (32) рассчитывается расстояние до точки экстремума.
Если расстояние до точки экстремума больше, чем расстояние, пройденное автопоездом в заданном интервале скоростей, то это означает, что экстремальное значение скорости при заданных условиях находится на большем расстоянии от начала движения. Расчеты следует продолжить для последующих заданных интервалов скоростей до выполнения условия υmax (максимальное в заданном диапазоне скоростей) > υэк (экстремальное значение скорости движения). Результаты расчета сведены в табл. 4.
В интервале скоростей 9–9,5 м/c при расчетном значении Т определение расстояние S до точки, в которой достигается максимальное значение скорости 9,5 м/c (по формуле (28)), не представляется возможным, так как подкоренные значения в формуле имеют отрицательную величину. Следовательно, υэ находится в интервале 9–9,5 м/c. Расстояние до точки экстремума скорости от точки, где скорости имеют минимальное в заданном интервале значение 9 м/c, определяется по формуле (32) и равно 41,01 м/c, экстремальное значение скорости движения – 9,34 м/c. Расстояние от точки начала движения со скоростью 8 м/c до точки, где достигается экстремальное значение скорости движения 78,17 м/c.
Затем показатели движения определяются в оставшейся части вертикальной кривой за точкой экстремума.
Заключение
Выведенные зависимости и методика расчетов позволяют определять показатели движения автопоездов с гидромеханической трансмиссией с учетом особенностей изменения тягового усилия от скорости движения. На основе предложенной методики и выведенных зависимостей предложен алгоритм и разрабатывается программа для моделирования движения автопоездов с таким видом трансмиссии на ПЭВМ.
Библиографическая ссылка
Скрыпник В.И., Кузнецов А.В., Питухин Е.А. ВЫВОД РАСЧЁТНЫХ ЗАВИСИМОСТЕЙ ДЛЯ ОПРЕДЕЛЕНИЯ СКОРОСТИ И ВРЕМЕНИ ДВИЖЕНИЯ ЛЕСОВОЗНЫХ АВТОПОЕЗДОВ НА БАЗЕ АВТОМОБИЛЕЙ С ГИДРОМЕХАНИЧЕСКОЙ ТРАНСМИССИЕЙ // Современные наукоемкие технологии. – 2019. – № 3-1. – С. 70-76;URL: https://top-technologies.ru/ru/article/view?id=37444 (дата обращения: 19.04.2024).