Научный журнал

Современные наукоемкие технологии

ISSN 1812-7320

"Перечень" ВАК

ИФ РИНЦ = 0,940

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Истомин А.Л. 1 Бадеников А.В. 1 Истомина А.А. 1

---

1 ФГБОУ ВО «Ангарский государственный технический университет»

Приведены математические модели задачи нахождения оптимальной структуры системы физической защиты периметра охраняемого объекта топливно-энергетического комплекса с помощью физических барьеров. В качестве критерия эффективности системы защиты периметра объекта принято время, затраченное нарушителем на преодоление физических барьеров. В первой модели находится такое количество физических барьеров различного типа на каждом рубеже охраны периметра объекта, при котором время преодоления физических барьеров периметра объекта внешним нарушителем достигает максимума. Модель второй задачи позволяет найти такую структуру системы защиты периметра объекта, при которой время преодоления нарушителем физических барьеров системы защиты не меньше заданного значения, а суммарная стоимость физических барьеров системы защиты периметра достигает минимального значения. Расчетными по моделям являются: время преодоления физических барьеров внешним нарушителем; оптимальная структура физических барьеров на каждом рубеже охраны периметра объекта; стоимость системы физических барьеров. Обе задачи сформулированы как задачи линейного программирования и могут быть решены симплексным методом линейного программирования. Приведены примеры решения задач с подробным выводом уравнений моделей оптимизационных задач и анализом полученного решения.

Статья в формате PDF

323 KB

система физической защиты

защита периметра объекта

модель системы физической защиты

защита топливно-энергетических объектов

1. Федеральный закон Российской Федерации от 12 февраля 2016 г. № 256-ФЗ «О безопасности объектов топливно-энергетического комплекса» [Электронный ресурс]. URL: http://base.garant.ru/12188188 (дата обращения: 12.01.2019).

2. Методические указания ОАО «НК «Роснефть «Оборудование объектов компании инженерно-техническими средствами охраны» П3-11.01 М-0003 версия 2.00. М., 2014. 114 с.

3. Степанов Б.П., Годовых А.В. Основы проектирования систем физической защиты ядерных объектов. Томск: Изд-во ТПУ, 2009. 118 с.

4. Истомин А.Л., Бадеников А.В. Определение оптимальной структуры системы физической защиты охраняемых объектов ТЭК // Экономика и менеджмент систем управления. 2018. Т. 27. № 1. С. 72–78.

5. Белоусов Е.Ф., Гордин Г.Т., Ульянов В.Ф. Основы систем безопасности объектов. Пенза: Изд-во ПГУ, 2000. 98 c.

В соответствии с Федеральным законом от 21 июля 2011 г. № 256-ФЗ «О безопасности объектов топливно-энергетического комплекса», одним из требований является обязанность субъектов топливно-энергетического комплекса (ТЭК) на стадиях проектирования и строительства объектов ТЭК предусматривать обязательное моделирование систем защиты будущих объектов в целях противодействия противоправным действиям, в том числе террористическим актам или покушениям на его совершение, угрожающие их безопасному функционированию. В результате моделирования должна быть предложена эффективная структура системы физической защиты (СФЗ), включающая инженерно-технические средства защиты и обнаружения несанкционированных действий, оптимальное количество постов и маршрутов охраны, требуемый штат охраны и его дислокация [1–3]. Проблемам проектирования систем физической защиты посвящены ряд работ [4, 5], однако вопросы эффективной защиты периметра территории охраняемых объектов в них отражены недостаточно.

Объекты ТЭК относятся к категории критической важности и повышенной опасности, имеют большие территории, которые должны быть защищены от доступа посторонних лиц и проникновения нарушителей с целью совершения хищения имущества или террористических актов. Поэтому одной из задач при проектировании CФЗ объектов ТЭК является эффективная защита периметров охраняемых объектов.

Защита периметра объекта – комплексная задача, для эффективного решения которой важно оптимальное сочетание физических барьеров (механических препятствий) – пассивного ограждения, затрудняющего и замедляющего проникновение нарушителя с техническими средствами обнаружения, обеспечивающими наиболее раннее установление попытки или факта преодоления периметра. В работе исследуется система защиты периметра объекта от внешнего нарушителя с помощью инженерно-технических средств защиты или физических барьеров (ФБ) с целью максимально замедлить движение нарушителя к цели. В этой связи в качестве критерия эффективности системы защиты периметра объекта принято время, затраченное нарушителем на преодоление физических барьеров. Математические модели задачи нахождения оптимальной структуры системы физической защиты сформулированы как задачи линейного программирования.

Математические модели задачи

Практически все физические барьеры сертифицированы по времени их преодоления. Следовательно, задача нахождения оптимального варианта защиты объектов физическими барьерами может быть сформулирована в виде, представленном ниже.

Модель 1. Пусть для защиты периметра объекта требуется организовать m рубежей защиты. Имеются n видов физических барьеров.

Обозначим через xij количество ФБ i-го вида на j-м рубеже, а через τij – время преодоления i-го вида барьерана j-м рубеже внешним нарушителем.

Тогда суммарное время преодоления физической защиты внешним нарушителем определяется как

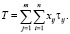(1)

Если затраты на сооружение (установку) одной единицы i-го вида барьера на j-м рубеже равны sij, то стоимость всех физических барьеров защищающих периметр объекта определяется как 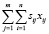. Поскольку построение СФЗ осуществляется в условиях ограниченных средств, то справедливо неравенство

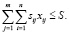(2)

Ограничениями в этой задаче могут быть требования, чтобы количество барьеров i-го вида на j-м рубеже было не меньше заданного значения Nij:

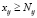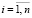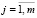, , . (3)

Кроме того, при построении ФБ могут существовать условия по комплектованию ФБ разных видов, например, если устанавливается внешнее предупредительное ограждение, оно обязательно дополняется капитальным ограждением с козырьком из армированной колючей ленты (АКЛ) или противоподкопным заглублением и т.п.

Эти условия могут быть представлены в виде

, ,

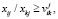
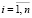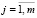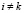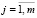, (4)

или после несложных преобразований в виде

, ,

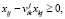
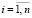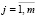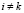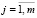, . (5)

Очевидно, что число ФБ разных видов не может быть отрицательной величиной

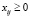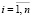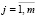, , . (6)

Таким образом, задача нахождения наилучшей структуры инженерно-технических средств защиты периметра объекта заключается в следующем: необходимо найти такие значения xij, 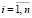, , 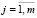при которых достигает максимума функция

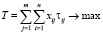(7)

и выполняются следующие ограничения

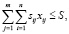(8)

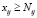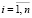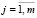, , , (9)

, ,

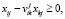
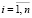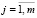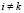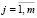, , (10)

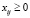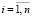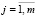, , . (11)

Требуется найти такие значения xij, удовлетворяющие ограничениям (8)–(11), при которых функция (7) будет максимальной.

Математическая модель задачи (7)–(11) относится к задачам линейного программирования и может быть решена симплексным методом линейного программирования.

Пример 1. Для защиты периметра объекта имеются следующие виды инженерно-технических средств: заграждение из сетки сварной, заграждение из сетки сварной с козырьком из АКЛ, бетонное капитальное заграждение, бетонное капитальное заграждение с козырьком из АКЛ, бетонное капитальное заграждение с козырьком из АКЛ с противоподкопным заграждением.

К системе физической защиты предъявляется требование организации не менее двух рубежей защиты периметра объекта, с не менее чем двумя заграждениями на каждом рубеже.

В таблице показаны стоимость защиты рубежа из заграждений различных видов и время их преодоления проломом внешним нарушителем [5].

Требуется определить оптимальный вариант защиты периметра объекта физическими барьерами из условия, что суммарные затраты на их оборудование и установку не должны превышать 11 млн руб.

Составим математическую модель задачи.

Если xij – количество ФБ i-го вида на j-м рубеже, а τij – время преодоления i-го вида барьера на j-м рубеже внешним нарушителем, то суммарное время преодоления физической защиты внешним нарушителем определяется как

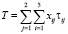(12)

или

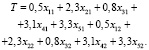(13)

Поскольку затраты на установку физических барьеров не должны быть больше заданных, запишем ограничение

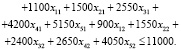(14)

В соответствии с требованиями к системе защиты на каждом рубеже должно быть не меньше двух заграждений.

Это условие для каждого рубежа можно записать в следующем виде:

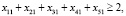(15)

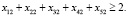(16)

В связи с тем, что число ФБ разных видов не может быть отрицательной величиной,

x11 ≥ 0, x21 ≥ 0, x31 ≥ 0, x41 ≥ 0, x51 ≥ 0,

x12 ≥ 0, x22 ≥ 0, x32 ≥ 0, x42 ≥ 0, x52 ≥ 0. (17)

Требуется найти такие значения xij, 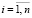, , 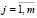удовлетворяющие ограничениям (14)–(17), при которых функция (13) будет максимальной.

Оптимальное решение: x11 = 0; x21 = 1; x31 = 0; x41 = 0; x51 = 0; x12 = 0; x22 = 1; x32 = 0; x42 = 2; x52 = 0.

Таким образом, первый рубеж следует укрепить заграждениями из сетки с козырьком из АКЛ и бетонным заграждением с козырьком из АКЛ, а второй рубеж – двумя рядами бетонных заграждений с козырьком из АКЛ. При данном варианте защиты обеспечивается максимальное время преодоления нарушителем защиты периметра объекта, которое составляет 11,6 минут.

Модель 2. Во многих случаях требуется организовать защиту объекта при минимальных расходах на установку физических заграждений. В этих случаях критерием эффективности является общая сумма затрат на систему защиты из физических барьеров, а ограничением является время преодоления нарушителем физических барьеров, которое не должно быть меньше заданного.

Если xij – количество ФБ i-го вида на j-м рубеже, то стоимость всех физических барьеров, защищающих периметр объекта, определяется как

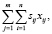(18)

где sij – затраты на сооружение (установку) одной единицы i-го вида барьера на j-м рубеже.

Если τij – время преодоления i-го вида барьера на j-м рубеже внешним нарушителем, тогда суммарное время преодоления физической защиты внешним нарушителем определяется как

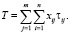(19)

Поскольку ожидаемое время преодоления нарушителем заграждений объекта должно быть не меньше заданного, запишем ограничение:

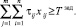(20)

Остальные ограничения остаются как в модели 1. Это и количество барьеров на каждом рубеже, и ограничения по комплектованию ФБ разных видов и т.д.

Тогда задача нахождения наилучшей структуры инженерно-технических средств защиты СФЗ заключается в следующем: необходимо найти такие значения xij, 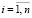, , 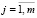при которых достигает минимума функция

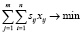, (21)

и выполняются следующие ограничения

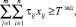(22)

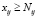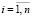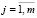, , , (23)

, ,

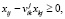
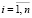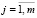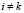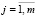, , (24)

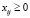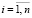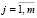, , . (25)

Требуется найти такие значения xij, удовлетворяющие ограничениям (22)–(25), при которых функция (21) будет минимальной.

Пример 2. На основании данных из примера 1 решим задачу нахождения оптимальной структуры СФЗ периметра объекта, при которой затраты на систему минимальны. Будем искать вариант защиты, при которой время преодоления рубежей защиты нарушителем будет не меньше 10 минут.

Остаются ограничения на то, что в системе защиты два рубежа и не менее двух барьеров на каждом рубеже.

Запишем выражение для критерия оптимальности:

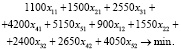(26)

Поскольку время на преодоление рубежей защиты должно быть не меньше 10 минут, запишем ограничение

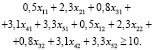(27)

Условия того, что на каждом рубеже должно быть не меньше двух барьеров, записываются в виде

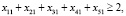(28)

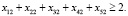(29)

В связи с тем, что число ФБ разных видов не может быть отрицательной величиной,

x11 ≥ 0, x21 ≥ 0, x31 ≥ 0, x41 ≥ 0, x51 ≥ 0,

x12 ≥ 0, x22 ≥ 0, x32 ≥ 0, x42 ≥ 0, x52 ≥ 0. (30)

Требуется найти такие значения xij, 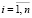, , 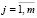удовлетворяющих, ограничениям (27)–(30), при которых функция (26) будет минимальной.

Оптимальное решение: x11 = 0; x21 = 2,34; x31 = 0; x41 = 0; x51 = 0; x12 = 0; x22 = 2; x32 = 0; x42 = 0; x52 = 0. Поскольку значение ограждений не может быть дробным, округлим решение до ближайшего целого значения.

Таким образом, и первый, и второй рубежи следует укрепить двумя заграждениями из сетки с козырьком из АКЛ.

При данном варианте защиты время преодоления заграждений нарушителем составит 9,2 минут, а стоимость заграждений – 6 млн 100 тыс. руб.

Видно, что не выполняется требование, согласно которому время преодоления защиты должно быть не меньше 10 минут. Округлим решение x21 = 2,34 до значения 3. Это значит, что первый рубеж укрепляется тремя, а второй рубеж – двумя заграждениями из сетки с козырьком из АКЛ. В этом случает, время преодоления заграждений нарушителем составит 11,5 минут, а стоимость заграждений – 7 млн 600 тыс. руб.

В целом решение показывает, что за значительно меньшие средства можно обеспечить сходную по показателю эффективности систему защиты. Так, в примере 2 мы нашли оптимальный вариант защиты, при котором время преодоления защиты нарушителем максимально. Оно составило 11,6 минут. Стоимость системы защиты для этого варианта составила 11 млн руб.

В то же время система стоимостью в 7 млн руб. 600 тыс. руб. позволила обеспечить время преодоления 11,5 минут, но ее стоимость на 3 млн 400 тыс. руб. меньше. Фактор стоимости может оказаться решающим, а сэкономленные средства можно направить на средства обнаружения и нейтрализации нарушителя.

Заключение

Представленные математические модели позволяют оценить эффективность СФЗ периметра охраняемого объекта и могут быть использованы для исследования эффективности проектируемой СФЗ. Расчетными по модели являются: время преодоления физических барьеров внешним нарушителем первого типа; оптимальная структура физических барьеров; стоимость системы физических барьеров.

Библиографическая ссылка