Усталостное разрушение – одно из самых распространенных видов замедленного разрушения стали, при котором происходит зарождение и постепенный рост начальных трещин до достижения ими критических размеров. Выявлено, что такой вид разрушения является основной причиной эксплуатационных повреждений большинства современных металлоконструкций и их сварных соединений.
Несмотря на то, что ответственные элементы таких конструкций подлежат периодическому техническому освидетельствованию, их усталостное разрушение часто протекает без видимых признаков. В связи с этим актуальной является проблема прогнозирования усталостного разрушения стальных деталей.
Цель исследования: определить методики, позволяющие оценить напряженно-деформированное состояние материала в докритический период развития усталостных трещин. Ее достижение известными методами современной теории связано со значительными математическими трудностями, в частности с решениями сложных нелинейных уравнений в частных производных. Усталость, как один из механизмов разрушения, является причиной эксплуатационных повреждений подавляющего большинства современных инженерных сооружений. Поэтому проблема сохранения прочности элементов конструкций при действии переменных нагрузок является одной из наиболее актуальных [1].
Материалы и методы исследования
Период докритического роста усталостной трещины определяет остаточную долговечность элемента конструкции. Стадия развития усталостной трещины в зависимости от конструктивных особенностей изделия (режимов его нагрузки, условий эксплуатации и др.) может составлять значительную часть общей долговечности элемента металлоконструкции. Поэтому исследование кинетики распространения усталостных трещин с учетом всех факторов влияния является важной научно-технической задачей и имеет большое практическое значение.
Как показывают экспериментальные исследования [2, 3], подавляющему большинству современных инженерных конструкций и сооружений присуще наличие макроскопических дефектов (трещины, разного рода несплошности, непровары в сварных соединениях, включения и др.), возникающих еще в процессе изготовления этих конструкций или появляющихся в процессе их эксплуатации.
В результате действия циклической нагрузки эти дефекты могут развиваться путем распространения трещин до полного разрушения элемента металлоконструкции, причем этот процесс может происходить при значительно меньшем предельном уровне нагрузки и характеризуется длительным накоплением необратимых повреждений в материале, что приводит к зарождению, развитию трещин и полному разрушению тела. Такое разрушение при циклической, то есть переменной во времени, нагрузке называется усталостным разрушением. Как правило, усталостное разрушение происходит непредсказуемо, часто без признаков поврежденности на поверхности металла элемента конструкции.
В сложном процессе усталостного разрушения достаточно четко просматриваются отдельные его стадии, отличающиеся необратимыми изменениями в материале. Общепринято разделять этот процесс на три основные стадии:
- инкубационный период, который характеризуется неоднородной концентрацией микропластических оползней, главным образом в поверхностных слоях деформируемого тела вследствие их повышенной технологической дефектности и пониженного сопротивления текучести;
- период зарождения субмикротрещины, слияния и образования минитрещин – нарушение структуры материала на уровне его блоков, зерен, включений, а в поверхностном слое – образование ступенек экструзии и интрузии;
- период распространения трещины, который начинается в тот момент, когда одна из микротрещин становится доминантной и перерастает в макротрещину. Контролирующим фактором распространения трещины является величина циклической пластической деформации в области пластической зоны у вершины трещины.
Исследование процессов, происходящих при усталостном развитии трещин, в первую очередь базируется на анализе напряженно-деформированного состояния (НДС) в месте расположения трещины. В границах механики разрушения, которая базируется на принципах идеальной упругости рассматриваемого тела и понимает трещину как разрез с толщиной равной нулю с поверхностью, на которой отсутствует напряжение, такая задача решается как краевая задача теории упругости [3].
Общий случай распределения изменений в радиусе произвольной точки О (рис. 1) границ трещины можно показать в виде трех видов изменений (рис. 2), которые находятся в соответствии главным видам смещений на поверхности этой трещины: нормального отрыва (I), поперечного (II) и продольного (III) смещения [4, 5].
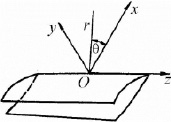
Рис. 1. Локальная система координат у вершины трещины
Первый представленный вид – это смещение верхних слоев трещины в разновекторных направлениях (симметрично к поверхностям ху и хz). Второй вид – это скольжение, в случае которого верхние слои трещины перемещаются один по другому в направлении, которое будет перпендикулярным по отношению к их фронту. Третий вид демонстрирует перемещение одного слоя трещины по-другому в направлении, параллельном фронту такой трещины.
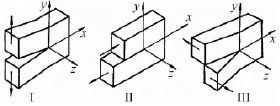
Рис. 2. Схема основных макромеханизмов распространения трещины
Согласно исследованиям А.Е. Андрейкива [4, 5] при реализации каждого из упомянутых типов деформирования распределение напряжений в окрестности контура трещины запишется в виде (1), (2), (3).
Для нормального отрыва [4, 5]:
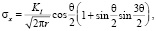
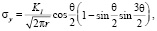(1)
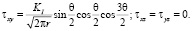
Для поперечного смещения [4, 5]:
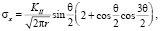
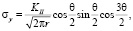(2)
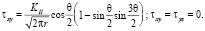
Для продольного смещения [4, 5]:
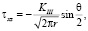
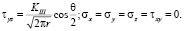(3)
Дополнительно в соотношениях (1), (2) необходимо принять σz = 0 для плоского напряженного состояния и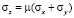 
для плоской деформации.
Таким образом, коэффициенты интенсивности напряжений являются основными расчетными характеристиками линейной механики разрушения, однозначно определяют НДС в зоне предразрушений.
При циклической нагрузке тела с трещиной анализ реальной механической ситуации в зоне предразрушения осложняется еще больше. Сложные процессы постепенного накопления повреждений во времени, сопровождающиеся непрерывным изменением реологических и прочностных свойств материала в этой зоне, практически не поддаются математическому описанию и могут быть смоделированы только в общих чертах.
Существование неупругих (пластичных) деформаций приводит к тому, что при разгрузке металлического материала, непосредственно у вершины трещины возникают остаточные напряжения сжатия, которые в свою очередь вызывают обратное пластическое течение материала. Таким образом, в некоторой части начальной зоны пластичности формируется область, где при циклических нагрузках происходит реверсивное течение, что приводит к накоплению пластических деформаций. Эта область и является, по сути, циклической пластической зоной.
Согласно некоторым качественным оценкам [4], ее размеры примерно в четыре раза меньше размеров пластической зоны при статической нагрузке. Наличие у вершины трещины зоны пластической деформации приводит к несоответствию настоящего НДС такому, что предполагается соотношениями, полученными при решении задачи для упругих тел.
Однако, если зона нелинейного поведения свойств материала достаточно мала, то существует область, которая по размерам является промежуточной между размерами пластической зоны и длиной трещины или размерами тела, в которой асимптотическое решение (1)–(3) еще описывает истинное распределение напряжений.
А поскольку в этом случае значения коэффициентов интенсивности напряжений полностью определяют поле напряжений вне зоны пластичности, то тем самым они контролируют напряженное состояние материала в середине этой области, а именно – интенсивность процессов разрушения, которые в ней происходят.
Таким образом, критерии линейной механики разрушения сохраняют свою прогнозирующую способность и в реальных ситуациях, если только выполняются условия малости пластических зон (условия квазихрупкого состояния). Необходимые ограничения, при которых указанные условия имеют место, устанавливаются специальными математическими соотношениями – условиями автомодельности [5].
Эти соотношения, в частности, являются основным критерием выбора оптимальных размеров образцов, при испытании которых разрушение происходит квазихрупким механизмом и тем самым обеспечивается адекватное определение характеристик трещиностойкости. Следует отметить, что развитие усталостных трещин происходит при сравнительно низких уровнях действующих напряжений и сопровождается меньшими, чем в статике, пластическими зонами.
Поэтому возможности применения коэффициентов интенсивности напряжений как расчетных параметров для описания усталостного разрушения значительно шире, чем при однократной (монотонной) нагрузке. Они могут быть эффективно использованы при расчете многих реальных инженерных объектов. В тех случаях, когда условия квазихрупкого разрушения не обеспечиваются, для расчета нужны более точные методы, учитывающие наличие развитых пластических зон у вершины трещины.
Для всех реальных материалов, при напряжениях превышающих σT, линейная связь между напряжениями и деформациями нарушается и дальнейшая нагрузка сопровождается пластическим течением. В результате этого перед концом трещины всегда существует пластическая зона определенных размеров. Для расчета этой зоны необходимо исследовать распределение напряжений и деформаций у вершины трещины в упруго-пластической постановке, что связано со значительными математическими трудностями.
Рассчитать в ней локальные напряжения возможно с помощью компьютерного математического моделирования напряженно-деформированного состояния методом конечных элементов (МКЭ).
Суть метода конечных элементов заключается в том, что тело представляется в виде некоторого каркаса, состоящего из элементов прямоугольной или треугольной формы. Совокупность элементов образует законченную решетку, внешняя форма которой соответствует форме тела.
Распределение напряжений в теле рассчитывают, рассматривая равновесие сил в общих точках или узлах решетки, а распределение деформаций – принимая во внимание перемещение обоих узлов.
Результаты исследования и их обсуждение
Авторами [6, 7] была разработана схема создания математической модели образца с надрезом, согласно которой исследуемый объект – идеализированная расчетная схема – система линейных алгебраических уравнений.
Непосредственный переход к расчетной схеме дает возможность естественно формулировать граничные условия, произвольно располагать узлы сетки элементов, сгущая ее в местах ожидаемого большого градиента напряжений и деформаций. Используемая модель позволяет рассчитывать напряжения, в том числе и в пластической зоне перед надрезом, с учетом эффекта упрочнения. Конечно-элементная сеть строится посредством стыковки любого числа фрагментов.
Графический образ сетки конечных элементов вблизи концентратора напряжений представлен на рис. 3.
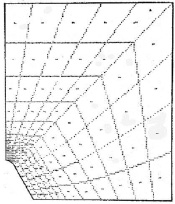
Рис. 3. Графический образ сетки конечных элементов вблизи концентратора напряжений [6]
Входные характеристики программы: предел текучести, модуль Юнга, показатель и коэффициент упрочнения определяется из испытаний на растяжение гладких образцов МРГ-3. В результате расчетов с помощью МКЭ определяется напряженно-деформированное состояние во всех узлах сетки конечных элементов.
С помощью этой методики можно определить локальные напряжения в зоне зарождения трещины по известному пределу текучести стали [7].
Выводы
Для любой заданной нагрузки можно определить локальное напряжение до и после образования пластически деформированной зоны разрушения.
Использование приемов математического моделирования напряженно-деформированного состояния стали и стальных деталей в местах формирования микротрещин предоставляет возможность диагностировать критические напряжения в местах зарождения трещин. Метод конечных элементов можно применять для определения докритического периода развития усталостных трещин.
Библиографическая ссылка
Шиховцов А.А., Михеев Г.В., Владимиренко А.С., Вербицкий Д.О. ОПРЕДЕЛЕНИЕ НАПРЯЖЕННО-ДЕФОРМИРОВАННОГО СОСТОЯНИЯ СТАЛИ ПРИ УСТАЛОСТНОМ РАЗРУШЕНИИ // Современные наукоемкие технологии. – 2019. – № 2. – С. 148-152;URL: https://top-technologies.ru/ru/article/view?id=37425 (дата обращения: 23.11.2024).