Углеродные ткани, ленты и волокна широко используются в ракетно-космическом производстве, авиастроении, автомобилестроении, что обусловлено их высокими удельными характеристиками [1, 2], хорошей стойкостью к воздействию повышенных температур, высокими антифрикционными характеристиками и т.д. Необходимость совершенствования эксплуатационных характеристик существующих углепластиков и других типов полимерных композитов на основе тканных армирующих материалов, приводит к необходимости расширения комплекса их свойств [3, 4]. Для придания углепластикам специальных (или, как полагают авторы работ [5, 6], функциональных свойств) используются технологии нанесения на поверхность углеродных тканей тонких металлических покрытий. Основной целью металлизации является изменение микроструктуры и физико-химических свойств поверхности тканей [7–9], что позволяет регулировать их реакционную способность, износостойкость, тепло- и электрофизические свойства, биосовместимость [10, 11] и др.
Авторами работ [5, 6] показано, что при использовании металлизированных углеродных лент в качестве армирующих материалов при изготовлении бандажей при ремонте поврежденных металлических трубопроводов в условиях отрицательных температур имеет место повышение механической прочности и долговечности. В работах [12, 13] приведены данные по повышению адгезионной прочности углепластиков при межслоевом сдвиге при использовании углеродной ленты с металлическим покрытием из нержавеющей стали. Авторы работ [14–16] показали, что после нанесения на технический текстиль тонких слоев металлических покрытий имеет место улучшение комплекса свойств, в том числе повышаются на 15–20 % показатели прочности, улучшаются характеристики драпируемости, износостойкости и др. Таким образом, металлизация углеродных тканей позволяет улучшить свойства углепластиков, однако в технической литературе отсутствуют данные по оптимальным значениям толщин металлических покрытий.
Целью настоящей работы является разработка методики и алгоритма оптимизации толщины металлического покрытия.
Материалы и методы исследования
В качестве объекта исследований использовалась отечественная однонаправленная углеродная лента ЛУП, на которую методом магнетронного распыления наносили металлическое покрытие из нержавеющей стали марки 12Х18Н10Т, титана ВТ1-0 и меди М1.
Перед нанесением металлического покрытия проводили плазмохимическую обработку углеродной ленты. Толщину покрытия определяли непосредственно на элементарной нити с помощью атомно-силового микроскопа марки SOLVER47PRO.
Механические испытания элементарных нитей проводили на разрывной машине марки Zwick//Roell.
Модель элементарной нити строили в программе SiemensNX, расчеты проводили в программном комплексе NX/Nastran. При построении геометрической модели принимали, что диаметр элементарной нити равен 6 мкм. К модели прикладывали нагрузку в виде распределенной растягивающей силы. С противоположной стороны образца использовалась заделка.
Результаты исследования и их обсуждение
Оптимизацию толщины металлического покрытия проводили методом последовательных уступок [17, 18] на основании результатов теоретических и экспериментальных исследований. В качестве критериев были использованы следующие характеристики: значения перемещений; линейная плотность; адгезионная прочность системы, элементарная нить-эпоксидная матрица и себестоимость покрытий при условии их нанесения методом магнетронного распыления на лабораторных установках. Оптимизацию проводили методом взаимных уступок. Характеристика адгезионной прочности принята за главный критерий, для которого определялось его экстремальное значение, и назначалась уступка. В соответствии с используемой «уступкой» задача решается еще раз, но при использовании второго по значимости критерия при условии, что отклонение первого критерия от его оптимального значения не превзойдет величины «уступки». Далее назначается «уступка» для второго критерия и т.д.
Алгоритм оптимизации толщины металлического покрытия показан на рисунке.
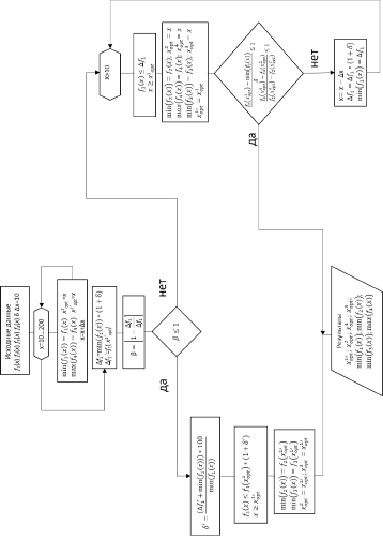
Алгоритм оптимизации толщины металлического покрытия
В работе использованы следующие обозначения: где: х – толщина металлического покрытия на углеродной ленте; δ – уступка; f1(x) – функция изменения величины деформационных свойств (перемещений) в зависимости от толщины металлического покрытия; x1opt – значение толщины покрытия, соответствующее оптимальному изменению перемещения; f4(x) – функция изменения адгезионной прочности; x4opt – значение толщины покрытия, соответствующее оптимальной величине адгезионной прочности; f2(x) и f3(x) – функции изменения плотности и себестоимости соответственно, которым соответствуют их оптимальные значения x2opt и x3opt.
Значения экстремальных величин и уступок по всем использованным критериям приведены в табл. 1.
Таблица 1
Значения показателей, используемых при оптимизации покрытия из нержавеющей стали 12Х18Н10Т
|
Толщина покрытия, нм |
Критерии |
Показатели |
|
|
Экстремальное значение |
Уступка, % |
||
|
10 50 70 100 150 200 |
Максимальные перемещения, мм |
0,265 0,252 0,247 0,241 0,232 0,225 |
7,1 |
|
10 50 70 100 150 200 |
Линейная плотность, текс×10-2 |
4,8 5,7 6,1 6,5 7,2 8 |
18,8 |
|
10 50 70 100 150 200 |
Адгезионная прочность, МПа |
90 110 115 120 100 85 |
0 |
|
10 50 70 100 150 200 |
Себестоимость руб/м2 |
190 230 250 270 310 350 |
22,9 |
Расположим критерии в порядке повышения их значимости: перемещения, плотность, адгезионная прочность, себестоимость. Определим минимальное значение главного критерия. Выберем уступку для главного критерия, приняв ее равной δ1 = 10 %.
Исходя из уступки δ1 минимальное значение перемещения будет равно
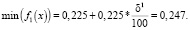
Что налагает следующее ограничение для второстепенных критериев:
f1(x) ≤ 0,247, т.е. x1opt1 ≥ 70.
Минимальное значение плотности при таком ограничении будет равно 6,1 и в 86 раз превосходит проигрыш по главному критерию, что доказывает правомочность выбранной уступки. Выигрыш по себестоимости также превосходит проигрыш по перемещению во много раз. Поскольку направленность критериев себестоимости и линейной плотности одинаковые, то нет необходимости выбирать уступку для себестоимости по линейной плотности, можно использовать то же самое значение x2opt и для определения себестоимости, которая составит 250.
С учетом уступки δ1 значение адгезионной прочности будет равно 115 МПа, что является проигрышем относительно максимального его значения 120 МПа при толщине 100 нм. Однако если рассматривать адгезионную прочность в качестве главного критерия и выбрать его оптимальное значение 120 МПа, то проигрыш по критерию перемещения составит 7,1 %. При такой уступке значение перемещения будет равно 0,241, что хуже первоначального значения перемещения (0,247) в 1,02 раза. Значение уступки уменьшится до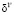 
= 7,1 %.
С учетом величины уступки (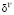
) будет иметь место следующее ограничение:
f1(x) ≤ 0,21;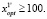 
При таком ограничении значение линейной плотности будет равно 6,5. Выигрыш по линейной плотности будет в 68 раз превышать проигрыш по перемещению. Значение себестоимости будет равно 270, а выигрыш по себестоимости также во много раз превосходит проигрыш по перемещению.
Таким образом, оптимальные значения перемещения – 0,241, плотности – 6,5, адгезионной прочности – 120 и себестоимости – 270 будут при толщине покрытия – 100 нм.
Поскольку характер изменения адгезионной прочности от толщины покрытия – нелинейный, а в его экстремуме значения остальных критериев лучше, чем при первоначальной уступке (10 %), рекомендуется вначале определять максимальное значение адгезионной прочности, при этом оценивая величину уступки по перемещению. Если модуль отношения значения перемещения при оптимуме адгезионной прочности к значению оптимума по перемещению будет меньше 1 (|β|<1), то можно использовать оптимальное значение толщины покрытия при максимальной адгезионной прочности. Иными словами, в этом случае мы получаем смещение оптимума в сторону адгезионной прочности, при котором мы не проигрываем по перемещению. В противном случае (при |β|>1) необходимо проводить оптимизацию методом уступок по первоначальной последовательности критериев: перемещение – линейная плотность – адгезионная прочность – себестоимость.
Для полученных значений показателей адгезионная прочность является главным критерием оптимизации. Соответственно, критерии оптимизации в порядке повышения их значимости будут располагаться следующим образом: адгезионная прочность, перемещения, плотность, себестоимость.
Аналогичным образом проведем расчеты для углеродной ленты ЛУП с покрытием из титана и меди (табл. 2).
Таблица 2
Значения показателей, используемых при оптимизации покрытия из титана ВТ1-0 и меди М1
|
Толщина покрытия, нм |
Критерии оптимизации |
Показатели |
|||
|
Экстремальное значение |
Уступка, % |
||||
|
Титан |
Медь |
Титан |
Медь |
||
|
10 50 100 150 200 |
Максимальные перемещения, мм |
0,273 0,264 0,256 0,250 0,245 |
0,274 0,265 0,257 0,251 0,246 |
4,49 |
4,47 |
|
10 50 100 150 200 |
Линейная плотность, текс×10-2 |
5,1 5,5 5,9 6,3 6,6 |
5,0 5,9 6,6 7,3 8,3 |
13,5 |
32 |
|
10 50 100 150 200 |
Адгезионная прочность, МПа |
80 95 105 90 85 |
88 105 115 100 85 |
0 |
0 |
|
10 50 100 150 200 |
Себестоимость руб/м2 |
210 260 300 340 380 |
200 240 280 320 360 |
30 |
40 |
Сравнение результатов, приведенных в табл. 1 и 2, показывает, что по всем исследуемым показателям (перемещение, плотность, адгезионная прочность и себестоимость) они близки между собой и поэтому использование дискретных критериев не приводит к изменению оптимального значения толщины. Для всех исследуемых материалов покрытий (нержавеющая сталь, титан и медь) она составляет 100 нм. При уменьшении толщины имеет место снижение адгезионной прочности, а при увеличении повышается себестоимость и плотность. Если задавать значения критериев в виде функций, то это позволило бы для каждого исследованного покрытия определить значение толщин более точно. Однако данный подход приведет лишь к увеличению продолжительности вычислений, но не изменит характера получаемых закономерностей.
Выводы
Приведены алгоритм и методика оптимизации толщины металлического покрытия на элементарных нитях, из которых изготовлена углеродная однонаправленная лента ЛУП методом взаимных уступок по критериям максимальной адгезионной прочности и минимальным значениям плотности, себестоимости и перемещениям. Для нанесения металлического покрытия использовался метод магнетронного распыления, с предварительной очисткой углеродной ленты. Для расчетов использовали результаты экспериментальных и теоретических исследований. Величины адгезионной прочности, себестоимости и плотности определяли экспериментально. Значения перемещений находили расчетным путем. В результате проведенных расчетов установлено, что при использовании в качестве покрытия всех исследуемых материалов (нержавеющей стали, титана и меди) оптимальным является покрытие толщиной 100 нм.
Результаты настоящей работы получены в рамках проекта по теме «Научные исследования по разработке композиционных материалов со структурой управляемого хаоса и их применение в высокотехнологичном производстве» по заданию № 11.7291.2017/БЧ.
Библиографическая ссылка
Нелюб В.А., Городецкий М.А. АЛГОРИТМ ОПРЕДЕЛЕНИЯ ОПТИМАЛЬНОЙ ТОЛЩИНЫ МЕТАЛЛИЧЕСКОГО ПОКРЫТИЯ ПРИ ИЗГОТОВЛЕНИИ УГЛЕПЛАСТИКОВ // Современные наукоемкие технологии. – 2019. – № 2. – С. 123-127;URL: https://top-technologies.ru/ru/article/view?id=37420 (дата обращения: 23.11.2024).