Для быстрого расчета доступности сетей, например, в специализированных САПР, необходимо получить модели сетевых устройств, позволяющие практически мгновенно получать необходимые характеристики задержек. Авторы предлагают «свёрточный» подход к моделированию, основанный на идентификации «импульсной характеристики» сетевого устройства (абстрактного обслуживающего прибора). Данная работа содержит метод, опубликованный ранее в [1], однако подвергнутый доработке, в частности, восстановление сигнала происходит не просто операцией свёртки, а посредством метода Гиллемина. Таким образом, отмеченный в [1] эффект падения амплитуды сигнала на выходе был компенсирован без введения в схему компенсирующего звена.
Рассматриваемую в исследовании систему можно описать с точки зрения теории стохастического управления. Для этого необходимо изучение непосредственно самого обслуживающего прибора, который представляет собой линейную одномерную систему. Одномерными являются системы с одной регулируемой величиной [2]. На вход устройство получает поток пакетов, которые генерируются через случайные интервалы времени. В качестве выходного сигнала имеется поток обработанных заявок. Некоторый оператор X преобразует входящий трафик и описывает функциональную зависимость между входным и выходным потоками заявок.
Таким образом, цель исследования сводится к определению оператора Х, так как он, действуя на входное распределение определенным способом и преобразовывая его в выходное, характеризует процесс обработки клиентских заявок абстрактным обслуживающим прибором.
Материалы и методы исследования
Под математической моделью объекта понимается описание функциональной зависимости между наблюдаемыми сигналами – оператор связи между функциями входных и выходных сигналов процесса. Построение таких моделей в основном осуществляется двумя способами: аналитическим и экспериментальным, а также путем их комбинаций.
Если из-за недостатка данных аналитическое описание объекта выполнить невозможно, применяют экспериментальные методы, в этом случае для построения модели используются непосредственно экспериментальные данные. В этом случае производится измерение входных и выходных сигналов системы, и модель формируется в результате обработки соответствующих данных [3].
В экспериментальном исследовании объектом изучения является сетевое устройство (маршрутизатор) в качестве линейной одномерной системы, на вход которой подается поток заявок, а на выходе имеется поток обработанных заявок. Поток заявок – это входящий трафик, который поступает на сетевое устройство через случайные промежутки времени. В качестве выходного сигнала рассматриваются временные интервалы между пакетами, прошедшими обработку сетевым устройством. Входящий поток заявок должен представлять собой эталонное воздействие на линейную систему. Для этого необходимо сгенерировать с помощью эталонного генератора случайных чисел набор равномерно распределённых величин – задержек между входящими запросами, которые и будут рассматриваться в качестве «белого шума».
Определение функциональной зависимости между входным и выходным сигналом осуществлялось путем проведения эксперимента. Две ЭВМ с операционной системой «Ubuntu» подключались к портам маршрутизатора (рис. 1).
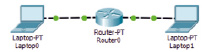
Рис. 1. Схема подключения ЭВМ к маршрутизатору
Далее производилась настройка маршрута обмена пакетами, файрволом блокировались все порты, кроме двух, подключенных к маршрутизатору. При отправке пакетов отправляющая ЭВМ является отправителем, а принимающая – приемником. После проведения каждого опыта данные ЭВМ менялись ролями. Все пакеты отправлялись через случайно сгенерированные промежутки времени в миллисекундах с помощью утилиты «hping». Фиксировались данные интервалы времени в текстовом файле утилитой «smokeping». С помощью утилиты «tcpdump» регистрировалось время получения пакета на принимающей ЭВМ и записывалось каждое новое значение в отдельный текстовый файл.
Далее был произведен расчет количества необходимых опытов. При расчете использовалось распределение Стьюдента, а искомое значение с заданной точностью вычислялось с помощью соотношения
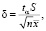(1)
где δ – заданная точность, tα – α-квантиль распределения Стьюдента, S – выборочная оценка стандартного отклонения,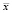 
– выборочная оценка среднего значения, n – число степеней свободы.
В соответствии с таблицей коэффициентов Стьюдента при α = 0,95 и полученного значения было найдено необходимое количество опытов. При коэффициенте Стьюдента равном 2,76 оптимальное количество опытов будет равно 5.
Результаты исследования и их обсуждение
По результатам пяти опытов было получено 10 текстовых файлов, разделенных на 2 группы: к первой группе относятся 5 файлов с находящимися в них 5000 величин – интервалами времени в миллисекундах, за которые генерировался каждый новый пакет. Во второй группе были 5 файлов, содержащие также по 5000 величин, но со значениями задержки каждого пакета маршрутизатором.
Импульсный отклик является важнейшей характеристикой системы и позволяет описать ее как «черный ящик», задав реакцию системы на некоторый простейший эталонный сигнал [4]. Таким образом, входной сигнал должен представлять собой эталонное воздействие на линейную систему, то есть являться «белым шумом». Термин «белый шум» обычно применяется к сигналу, имеющему автокорреляционную функцию, математически описываемую дельта-функцией Дирака по всем измерениям многомерного пространства, в котором этот сигнал рассматривается. Данное статистическое свойство является основным для сигналов такого типа [5]. Величина лага для построения АКФ равна 50. Вид входного сигнала первого опыта и его автокорреляционная функция показаны на рис. 2 и 3 соответственно.
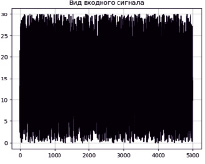
Рис. 2. Вид входного сигнала первого опыта
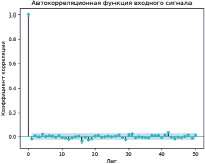
Рис. 3. АКФ входного сигнала первого опыта
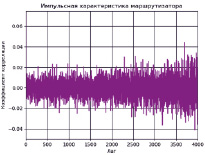
Рис. 4. Импульсная характеристика маршрутизатора
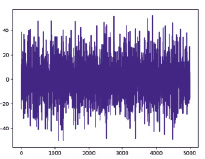
Рис. 5. Восстановленный методом Гиллемина вид выходного сигнала
Полученный график АКФ входного сигнала в некотором приближении напоминает дельта-функцию Дирака. Таким образом, данный сигнал можно рассматривать в качестве белого шума [6].
Взаимная корреляционная функция (ВКФ) двух различных сигналов описывает степень сходства их формы, а также их смещение друг относительно друга по времени. ВКФ представляет собой импульсную характеристику устройства, то есть отклик линейной системы на эталонное воздействие при нулевых начальных условиях.
После проведения 5 опытов было получено две группы наборов задержек: между входными запросами и между заявками, обработанными маршрутизатором. Используя полученные данные, были определены пять ВКФ выходного сигнала. По совокупности пяти ВКФ была вычислена усредненная импульсная характеристика устройства (рис. 4).
Для восстановления вида выходного сигнала был использован метод Гиллемина. Согласно данному подходу, аппроксимирующая частотную характеристику функция или её производные выражаются как последовательность бесконечно коротких импульсов. Данная последовательность представляет собой заданную функцию в квантованной форме. Вероятность ошибки в данном способе восстановления сигнала в основном связана со ступенчатым характером аппроксимирующей функции [7]. Найденная частотная характеристика аппроксимируется кусочно-линейным образом, далее два последовательных дифференцирования сводят аппроксимирующую функцию к последовательности бесконечно коротких импульсов. Окончательное выражение для искомой функции времени f(t) имеет вид
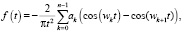(2)
где ak – величина k ступени производной частотной характеристики, wk – координата ступеней на частотной оси.
Тогда восстановленный выходной сигнал будет иметь вид (рис. 5).
Значение эмпирической функции распределения в точке х равно доле результатов наблюдений в выборке, меньших х [8]. Для проверки гипотезы H0 создано много непараметрических методов – критерии Смирнова, типа омега-квадрат (Лемана – Розенблатта), Вилкоксона (Манна – Уитни), Ван-дер-Вардена, Сэвиджа, хи-квадрат и другие. Распределения статистик всех этих критериев при справедливости H0 не зависят от конкретного вида совпадающих функций распределения F(x) °G(x) [9].
Оценка погрешности восстановленного сигнала производилась по критерию согласия Смирнова. Проверяемая нулевая гипотеза имеет вид H0: F1(x) = F2(x) против конкурирующей H0: F1(x) ≠ F2(x) [10].
Статистика критерия Смирнова для сравнения двух эмпирических функций имеет вид
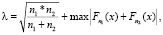(3)
где Fn1(x) и Fn2(x) – эмпирические функции распределения, построенные по двум выборкам c объемами n1 и n2 соответственно. Гипотеза H0 отвергается, если фактически наблюдаемое значение статистики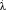 
больше критического 
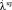, т.е. 
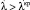, и принимается в противном случае.
При n1, n2 ≥ 50 распределение статистики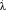 
сводится к распределению Колмогорова для статистики λ. Тогда гипотеза H0 опровергается на уровне значимости a, если фактически наблюдаемое значение 
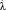больше критического λα, т.е. 
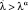, и принимается в противном случае.
Объем каждой выборки 4999 значений. Выборки разбиты на 20 интервалов, начальное значение является минимальным из двух выборок, а конечным – самое большое. Первым шагом является вычисление частот значений в каждом интервале для каждой выборки, n1 и n2 соответственно. Затем необходимо посчитать накопленные частоты двух эмпирических функций для каждого интервала, обозначим их как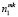 
и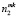 
соответственно. Из полученных частот вычисляются значения их эмпирических функций распределения: 
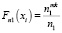и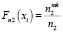 
. Затем производится расчет модуля разницы между ними и находится его максимальное значение по формуле (4) из [10]:
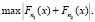(4)
Для данных функций распределения максимальный модуль разницы получился равным 0,136.
Подставляя полученные значения в формулу статистики критерия Смирнова, получаем λ = 6,79 для уровня значимости α = 0,25 λ = 6,8. Так как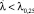 
, то принимается нулевая гипотеза H0, следовательно, обе выборки принадлежат одной и той же функции распределения [11].
Заключение
В ходе данной работы был представлен метод определения импульсной характеристики сетевого устройства. По результатам проведенного эксперимента была найдена импульсная характеристика маршрутизатора, а также выполнено восстановление вида выходного сигнала по частотной характеристике методом Гиллемина. Согласно критерию Смирнова гипотеза справедлива при уровне значимости α = 0,25.
Данная статья подготовлена в рамках выполнения научно-исследовательских работ, поддержанных грантами Российского фонда фундаментальных исследований № 16-47-330055, № 18-07-01109.
Библиографическая ссылка
Монахов Ю.М., Кузнецова А.П., Леткова Н.С., Шобин С.В. О ВОЗМОЖНОСТИ ПРИМЕНЕНИЯ ИМПУЛЬСНОЙ ПЕРЕДАТОЧНОЙ ФУНКЦИИ ДЛЯ МОДЕЛИРОВАНИЯ ПОВЕДЕНИЯ СЕТЕВОГО УСТРОЙСТВА // Современные наукоемкие технологии. – 2019. – № 2. – С. 110-113;URL: https://top-technologies.ru/ru/article/view?id=37418 (дата обращения: 23.11.2024).