В связи с ростом научно-прикладного интереса к тематике применения беспилотных летательных аппаратов (БПЛА) мультироторного типа увеличивается потребность в получении и использовании универсальных математических моделей, описывающих движение БПЛА с различной степенью полноты этих описаний [1]. Большинство авторов предпринимает попытки описания движения БПЛА с помощью систем линеаризованных уравнений, поскольку для нелинейных уравнений затруднен аналитический синтез системы управления [2, 3]. Описание математической модели движения БПЛА с помощью уравнений Ньютона – Эйлера с учетом перекрестных связей представлено в [4–6]. C помощью обобщенных координат и метода Лагранжа формируется математическая модель движения БПЛА в работе [7]. Линеаризованные и упрощенные модели движения БПЛА лежат в основе синтеза регуляторов и фильтров: LQR-регуляторов [8], LQG-регуляторов [9], фильтра Калмана [10], L1-оптимизации [11]; управление со скользящим режимом [12, 13]. В работе [14] рассматривается синтез регуляторов с помощью линеаризации обратной связью.
В большинстве работ после получения систем управления, синтезированных с использованием упрощенных моделей, не выполняется оценка влияния исключенных из рассмотрения факторов. При синтезе систем автоматического управления движением БПЛА с использованием упрощенных моделей необходимо учитывать их адекватность.
Цель работы – получение модели, учитывающей влияние перекрестных связей, и оценка этого влияния на точность модели.
Математическая модель движения БПЛА
На рис. 1 показаны взаимные расположения нормальной земной и связанной систем координат, положительные направления отсчета углов рыскания, тангажа и крена, сила тяги и моменты, создаваемые винтами, направления вращения винтов.
Переход из связанной системы координат (с.к.) в нормальную земную с.к. возможно выполнить с использованием матрицы перехода [15]:
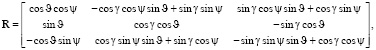
где ϑ – угол тангажа, γ – угол крена, ψ – угол рыскания.
При моделировании БПЛА приняты следующие допущения: БПЛА симметричен; центр масс расположен в начале координат связанной системы; коэффициенты силы тяги винтов равны; коэффициенты моментов, создаваемых винтами, равны. Перекрестные связи представлены гироскопическими моментами, возникающими при вращении БПЛА.
В силу симметрии тензор инерции БПЛА имеет вид
где Ix, Iy, Iz – осевые моменты инерции БПЛА.
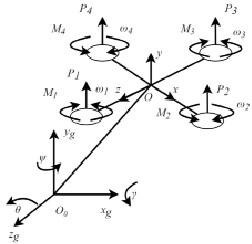
Рис. 1. Системы координат
Сила тяжести в земной с.к.: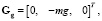 
где m – масса БПЛА, g – ускорение силы тяжести. Сила сопротивления воздуха в земной с.к.: 
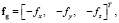где fx, fy, fz – проекции силы сопротивления воздуха в земной с.к. Сила тяги в связанной с.к.:
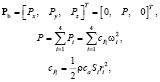(1)
где P – суммарная тяга, Pi – сила тяги i-го винта,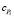 
или ki – коэффициент силы тяги i-го винта, ri – радиус i-го винта, Si – площадь ометаемой лопастями i-го винта поверхности, р – плотность воздуха, ca – коэффициент подъемной силы винта.
Сила тяги в нормальной земной с.к.: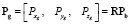 
.
Уравнение динамики движения центра масс БПЛА в нормальной земной с.к.:
.
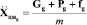Уравнение динамики движения ц.м. БПЛА в нормальной земной с.к. в проекциях на оси этой с.к.:
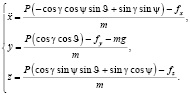(2)
Угловая скорость вращения БПЛА в связанной с.к.: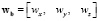 
, где wx, wy, wz – проекции вектора угловой скорости аппарата в связанной с.к. Производная угловой скорости вращения БПЛА в связанной с.к.: 
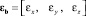, где εx, εy, εz – проекции производной вектора угловой скорости аппарата в связанной с.к.
Вектор кинетического момента: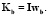 
Производная кинетического момента: 
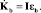Изменение кинетического момента: 
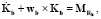где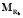 
– результирующий момент в связанной с.к.
Уравнения динамики углового движения в связанной с.к. можно записать в виде
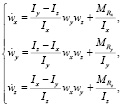(3)
где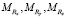 
– проекции результирующего момента.
Результирующий момент состоит из момента, создаваемого винтами, и гироскопических моментов двигателей и винтов. В этой работе инерционность винтов не учитывается.
Проекции результирующего момента с учетом моментов, создаваемых винтами, гироскопических моментов двигателей и винтов и возмущающих моментов определяются как сумма соответствующих проекций:
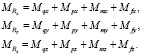(4)
Используя кинематические уравнения Эйлера, изменения углов Эйлера определяются через проекции угловой скорости следующим образом:
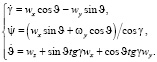(5)
Таким образом, система нелинейных дифференциальных уравнений в форме Коши имеет следующий вид:
(6)
где x1 = x,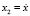 
, x3 = y, 
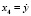, x5 = z, 
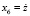, x7 = wх, 
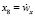, x9 = wy, 
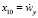, x11 = wz, 
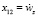, x13 = γ, x14 = ψ, x9 = wy, x15 = ϑ.
Математическая модель БПЛА (6) без учета возмущений и перекрестных связей в связанной системе координат в форме Коши может быть записана следующим образом:
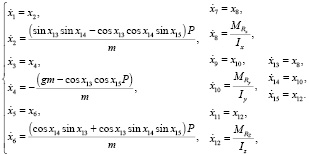(7)
Упрощенная математическая модель (7) может быть записана следующим образом:
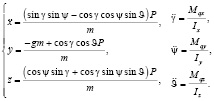(8)
Сила тяги и управляющие моменты для системы уравнений (8):
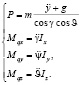(9)
Квадраты угловых скоростей вращения винтов, необходимые для создания управляющих моментов и силы тяги, могут быть выражены следующим образом:
(10)
Таким образом, задача управления БПЛА может быть сведена к задаче определения потребных силы тяги и управляющих моментов.
Выполним линеаризацию математической модели движения БПЛА в пространстве без учета перекрестных связей и возмущений (7) в соответствии с [16]:
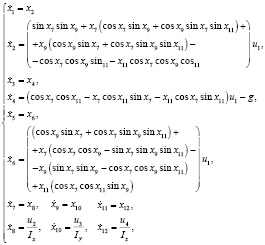(11)
где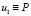 
, 
, 
, 
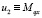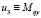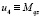; здесь аргументы тригонометрических функций имеют смысл выбранной рабочей точки.
Для нулевой рабочей точки (11) примет вид
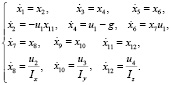(12)
Из анализа (12) следует, что для линеаризованной модели при нулевых начальных условиях возможно выполнить разделение на движение в двух ортогональных вертикальных плоскостях и независимое движение вокруг ц.м. по каналам тангажа, крена и рыскания. При этом для линеаризованной модели канал рыскания не оказывает влияния на движение в вертикальной плоскости и может рассматриваться отдельно.
Математическая модель движения БПЛА в вертикальной плоскости может быть получена из упрощенной математической модели движения БПЛА в пространстве (12).
В силу симметрии аппарата рассмотрим движение вдоль оси x:
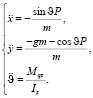(13)
Выполним замену переменных и запишем систему уравнений (13) в форме Коши:
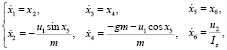(14)
где x1 – боковое перемещение, x2 – скорость бокового перемещения, x3 – высота, x4 – скорость изменения высоты, x5 – угол тангажа, x6 – скорость изменения угла тангажа, u1 – управляющее ускорение (сила тяги), u2 – управляющий момент.
Выполним линеаризацию математической модели движения БПЛА в вертикальной плоскости (14) в соответствии с [17]:
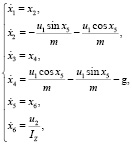(15)
здесь аргументы тригонометрических функций имеют смысл выбранной рабочей точки.
Для нулевой рабочей точки (15) примет вид
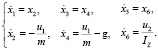(16)
Исходные данные для моделирования
Моделирование выполняется для систем уравнений (6) и (7) для последующего анализа и сравнения движения БПЛА с учетом и без учета перекрестных связей.
При выполнении моделирования используются исходные данные, представленные в табл. 1. Эти данные аналогичные исходным данным в [18]. Аэродинамическое сопротивление при отсутствии возмущений носит диссипативный характер и при моделировании не учитывалось. На управляющие ускорения по каналам крена uγ, рыскания uψ и тангажа uϑ наложены ограничения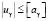 
, 
, 
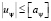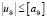соответственно. На желаемое ускорение, создаваемой силой тяги наложено ограничение 
.
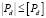Желаемые значения углов тангажа и крена изменялись во времени следующим образом:
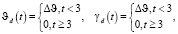(17)
где Δϑ – желаемое значение угла тангажа и крена.
Система управления ориентацией БПЛА построена с использованием двух ПИД-регуляторов для канала крена и тангажа. Для обоих каналов используются коэффициенты: kP = 4, kD = 4. Управление по каналу рыскания не производится.
Желаемые управляющие моменты по каналам крена и тангажа можно определить:
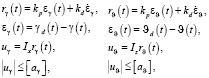
при этом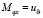 
, 
, 
.
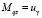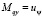Система управления движением ц.м. БПЛА построена с использованием ПД-регулятора для канала высоты: kP = 6, kD = 4,5. Отсюда желаемая сила тяги:
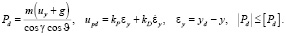
По полученным желаемым управляющим ускорениям и силе тяги по (10) вычисляются необходимые угловые скорости вращения винтов.
Таблица 1
|
Параметр |
Значение |
Размерность |
|
g |
9,81 |
м/с2 |
|
m |
0,468 |
кг |
|
l |
0,225 |
м |
|
k |
2,98•10-6 |
рад |
|
b |
1,140•10-7 |
рад |
|
IM |
3,357•10-5 |
кг×м2 |
|
Ix |
4,856•10-3 |
кг×м2 |
|
Iy |
8,801•10-3 |
кг×м2 |
|
Iz |
4,856•10-3 |
кг×м2 |
|
ωi |
[300, 900] |
рад/с |
|
[aγ], [aψ], [aϑ] |
1 |
рад/с2 |
|
[uy] |
19,62 |
м/с2 |
Моделирование движения БПЛА выполнялось в программном пакете MATLAB. В качестве метода численного интегрирования использовался метод Эйлера с фиксированным шагом 0,001 с.
Результаты моделирования движения БПЛА
На рис. 2 представлены результаты моделирования движения БПЛА с учетом и без учета перекрестных связей.
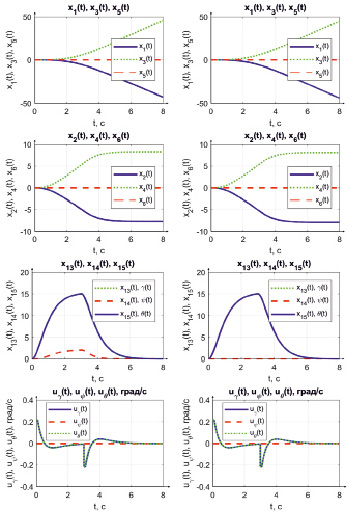
Рис. 2. Результаты моделирования движения БПЛА с учетом перекрестных связей (слева) и без учета перекрестных связей (справа)
Оценка влияния перекрестных связей на движения БПЛА производится по двум критериям: Δψ – значение угла рысканья в конце моделирования для модели, описываемой системой уравнений; Δε – «промах», расстояние между положением БПЛА в горизонтальной плоскости в конце моделирования для моделей, описываемых системами уравнений и соответственно.
Желаемое значение углов тангажа и крена Δϑ изменяется от 0 ° до 25 ° с шагом 1 °.
На рис. 3 представлены: зависимость величины критерия Δψ от Δϑ, зависимость величины критерия Δε от Δϑ и зависимость величины критерия Δε от дальности перелета р в конце моделирования. Зависимости были интерполированы на интервале между точками.
Из анализа рис. 3 следует, что с увеличением желаемого угла тангажа происходит нелинейный рост угла рыскания и нелинейный рост «промаха». При этом при значении желаемого угле тангажа более 10 ° «промах» превышает 1 м на расстоянии 102,1 м от точки (0;0) (11 °– 1,257 м).
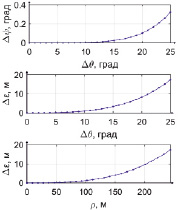
Рис. 3. Оценка влияния перекрестных связей на движение БПЛА
Заключение
Разработана математическая модель БПЛА как объекта управления с учетом и без учета возмущений и перекрестных связей в пространстве. Получена математическая модель движения БПЛА в вертикальной плоскости. Получены линеаризованные математические модели движения БПЛА в пространстве и в вертикальной плоскости. Выполнено моделирование движения БПЛА в пространстве с учетом и без учета перекрестных связей и проведена оценка влияния этих связей.
По результатам моделирования можно сделать рекомендации по использованию полученной системы с учетом перекрестных связей, поскольку данная система повышает точность описания движения квадрокоптера.
Работа выполнена при поддержке гранта ФГБУ «Фонд содействия развитию малых форм предприятий в научно-технической сфере» (Фонд содействия инновациям) (Договор № 12089ГУ2/2016).
Библиографическая ссылка
Карпунин А.А., Титков И.П. УПРОЩЕНИЕ И ЛИНЕАРИЗАЦИЯ МАТЕМАТИЧЕСКОЙ МОДЕЛИ ДВИЖЕНИЯ БЕСПИЛОТНЫХ ЛЕТАТЕЛЬНЫХ АППАРАТОВ В ПРОСТРАНСТВЕ И В ВЕРТИКАЛЬНОЙ ПЛОСКОСТИ // Современные наукоемкие технологии. – 2019. – № 2. – С. 69-77;URL: https://top-technologies.ru/ru/article/view?id=37411 (дата обращения: 23.11.2024).