В современных реалиях активно развиваются подходы к автоматизации химического производства. Сфера образования не стала исключением. За последние несколько лет было разработано и введено в эксплуатацию множество систем, автоматизирующих различные химические задачи: поиск результатов химических реакций, балансировка, расчет концентрации растворов и т.д. Большинство подобных сервисов и систем реализованы в виде Web-приложений и доступны повсеместно в сети Интернет.
При проектировании собственной системы очень важно разработать эффективный алгоритм решения определенной задачи, который был бы одновременно и быстрым и использовал минимум памяти. Такая проблема может возникнуть, например при реализации модуля балансировки химического уравнения.
Химические уравнения играют особую роль как в теоретической, так и в промышленной химии. Каждое химическое уравнение описывает некоторую химическую реакцию. Вещества, первоначально участвующие в реакции, называются реагентами, а вновь образовавшиеся – продуктами.
Процесс балансировки химических уравнений, который заключается в поиске стехиометрических коэффициентов, является одним из важнейших в промышленной химии. Специалисты, занимающиеся балансировкой, в основном используют эвристический метод, который рационален лишь для простых химических реакций [1].
В экспертных системах или сервисах, которые направлены на автоматизацию решения различных химических задач, на смену эвристике приходят математические методы поиска стехиометрических коэффициентов.
Один из математических методов, описанный профессором Хирематом Сурешем из Индийского технологического института Брахмадевадра Мане, предполагает представление химического уравнения в виде системы линейных уравнений и последующего ее решения методом Гаусса [2]. Однако алгоритм, предложенный профессором, не является эффективным для решения задачи на компьютере, так как дальнейший вывод конечного результата усложняет алгоритм.
Метод, основанный на поиске ядра матрицы, который предложил Лоуренс Торн из Сандийских национальных лабораторий, не подходит для реализации на компьютере из-за его сложности [3].
Таким образом, появляется необходимость поиска более эффективного алгоритма для решения задачи. Использование метода Гаусса – Жордана в конечном счете может заменить большинство операций преобразований всего лишь нахождением наименьшего общего кратного знаменателей вектора решений системы.
Цель работы: разработка эффективного алгоритма поиска стехиометрических коэффициентов химического уравнения. Для несбалансированной химической реакции требуется найти стехиометрические коэффициенты, используя метод Гаусса – Жордана.
Алгоритм решения задачи
Пусть дана некоторая несбалансированная химическая реакция:
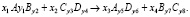(1)
где х1 – х4 – искомые стехиометрические коэффициенты; А, В, С – участвующие в реакции вещества; у1 – у8 – количество атомов каждого вещества в молекулах, участвующих в реакции.
В соответствии с количеством участвующих элементов в реакции, составляются линейные уравнения
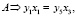
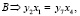(2)
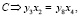
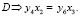
На основе составленных линейных уравнений формируется система
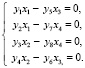(3)
Далее система записывается в виде матрицы и решается методом Гаусса – Жордана. Этот метод предназначен не только для решения систем линейных уравнений, но и для нахождения обратной матрицы [4]. Первый этап метода – прямой ход, он аналогичен методу Гаусса. Второй этап – обратный ход, он заключается в обнулении всех элементов матрицы коэффициентов системы линейных уравнений, выше ведущих элементов [5].
Решением системы будет являться вектор решений, где последний элемент – произвольное действительное число, которому присваивается единица. Каждый элемент вектора решений системы приводится к обыкновенным дробям. Для всех знаменателей дроби ищется наименьшее общее кратное, значение которого затем умножается на каждый элемент вектора. Таким образом полученные значения и будут являться искомыми стехиометрическими коэффициентами химического уравнения.
Предложенный алгоритм можно применить для всех простых химических реакций (мономолекулярные, бимолекулярные, тримолекулярные). Рассмотрим пример для несбалансированной мономолекулярной реакции:
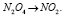(4)
Представим химическую реакцию в математической форме:
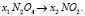(5)
В соответствии с веществами, которые участвуют в реакции, составим два линейных уравнения:
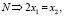
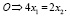(6)
На их основе составим систему линейных уравнений:
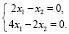(7)
Запишем систему в виде матрицы и решим ее методом Гаусса – Жордана:
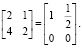(8)
В данном случае будет всего два решения –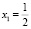 
, x2 – произвольное действительное число, которому присваивается единица, а при переводе в обыкновенную дробь 
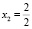. Применив алгоритм НОК для всех знаменателей, получим число, на которое умножим решения системы. В данном случае это число равно двойке. x1 = 1, x2 = 2. Подставив полученные коэффициенты в уравнение, получим сбалансированную реакцию
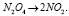(9)
Рассмотрим пример для несбалансированной бимолекулярной реакции
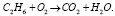(10)
Представим химическую реакцию в математической форме:
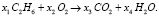(11)
В соответствии с веществами, которые участвуют в реакции, составим три линейных уравнения
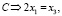
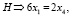(12)
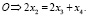
На их основе составим систему линейных уравнений:
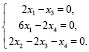(13)
Запишем систему в виде матрицы и решим ее методом Гаусса – Жордана:
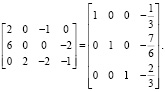(14)
Данная система имеет четыре решения –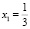 
, 
, 
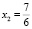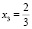, x4 – произвольное действительное число, которому присваивается единица, а при переводе в обыкновенную дробь 
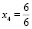. Применив алгоритм НОК для всех знаменателей получим число, на которое умножим решения системы. В данном случае это число равно шести. x1 = 2, x2 = 7, x3 = 4, x4 = 6. Подставив полученные коэффициенты в уравнение, получим сбалансированную реакцию:
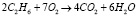. (15)
Рассмотрим пример для несбалансированной тримолекулярной реакции:
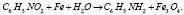(16)
Представим химическую реакцию в математической форме:
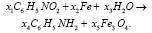(17)
В соответствии с веществами, которые участвуют в реакции, составим пять линейных уравнений:
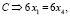
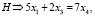
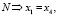(18)
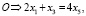
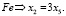
На их основе составим систему линейных уравнений
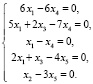(19)
Запишем систему в виде матрицы и решим ее методом Гаусса – Жордана:
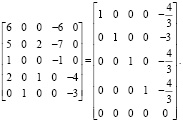(20)
Данная система имеет пять решений – x1, x3,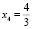 
, x2 = 3, x5 – произвольное действительное число, которому присваивается единица, а при переводе в обыкновенную дробь 
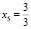. Применив алгоритм НОК для всех знаменателей, получим число, на которое умножим решения системы. В данном случае это число равно трем. x1, x3, x4 = 4, x2 = 9, x5 = 3. Подставив полученные коэффициенты в уравнение, получим сбалансированную реакцию:
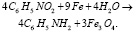(21)
Алгоритм в общем виде, изображенный в виде блок-схемы, представлен на рис. 1.
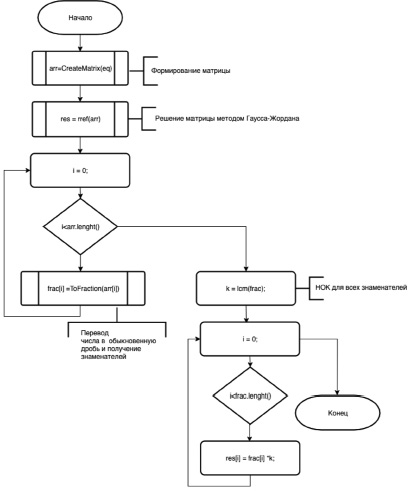
Рис. 1. Блок-схема алгоритма
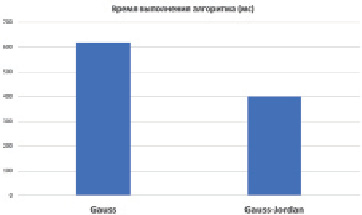
Рис. 2. Сравнение времени выполнения алгоритмов
Анализ результатов
Разработанный алгоритм поиска стехиометрических коэффициентов химического уравнения на основе метода Гаусса – Жордана улучшает метод, предложенный профессором Хирематом Сурешем, и применим для всех простых химических реакций. Реализация алгоритма на компьютере позволит достичь результатов за меньшее количество времени, чем при решении данной задачи методом Гаусса. Сравнение времени выполнения алгоритмов представлено на рис. 2.
Алгоритм протестирован на мономолекулярных, бимолекулярных и тримолекулярных реакциях и может быть использован при разработке сервисов и сложных систем для автоматизации химических задач в сфере образования или на производстве.
Библиографическая ссылка
Николюкин М.С. РАЗРАБОТКА АЛГОРИТМА ПОИСКА СТЕХИОМЕТРИЧЕСКИХ КОЭФФИЦИЕНТОВ ХИМИЧЕСКИХ УРАВНЕНИЙ // Современные наукоемкие технологии. – 2019. – № 1. – С. 99-103;URL: https://top-technologies.ru/ru/article/view?id=37386 (дата обращения: 18.04.2024).