В научно-исследовательской деятельности и в инженерной практике часто возникают задачи, связанные с аналитической обработкой экспериментальных данных. Все задачи такого рода объединяет наличие массивов исходных данных, характеризующих состояние и динамику изменения параметров исследуемых объектов или процессов. Построение математических моделей по экспериментальным данным заключается в определении аналитической зависимости, т.е. подборе такой эмпирической формулы, вычисления значений по которой в максимально возможной степени соответствовали бы данным, полученным опытным путем [1]. При этом должны быть учтены случайные отклонения измеряемых величин. Для решения такого рода задач на первом этапе необходимо установить вид зависимости и, соответственно, определить вид аппроксимирующей функции, зависящей от одной или нескольких переменных в соответствии с имеющимися массивами исходных данных, полученных экспериментальным путем. В случае отсутствия каких-либо теоретических предпосылок для определения вида аппроксимирующей функции, обычно выбирают функциональную зависимость из числа наиболее простых, сравнивая их графики с графиком результатов эксперимента [2]. При этом во многих случаях ограничиваются полиномом. В зависимости от количества параметров, определяемых размерностью массива экспериментальных данных, в качестве аппроксимирующей будет выбрана функция одной или от нескольких переменных.
В настоящее время одним из популярных инструментальных средств, позволяющих эффективно решать такого рода задачи, не прибегая к использованию языков программирования, является табличный процессор, в состав которого включена группа специальных проблемно-ориентированных функций для анализа данных [3].
Цель исследования: повышение эффективности процесса анализа экспериментальных данных в проектах VB.NET посредством интеграции функций табличного процессора MS Excel, что позволит исключить непосредственное программирование алгоритмов их обработки.
Материалы и методы исследования
Аппроксимация экспериментальных данных функцией одной переменной в MS Excel осуществляется путем построения точечного графика (х – имеет конкретные значения) с последующим подбором подходящей аппроксимирующей функции. Для осуществления аппроксимации на диаграмме экспериментальных данных необходимо построить линию тренда, выбрав в контекстном меню пункт «Добавить линию тренда» и в появившемся диалоговом окне указать вид аппроксимирующей функции. Здесь же задается параметр, который позволяет «увидеть» на диаграмме аналитический вид аппроксимирующей функции и достоверность аппроксимации.
В тех случаях, когда аппроксимирующая переменная y зависит от нескольких независимых переменных (y = f(x1, x2,..., xn)), подход с построением линии тренда не дает решения. В таких случаях могут быть использованы специальные функции MS Excel ЛИНЕЙН и ЛГРФПРИБЛ (табл. 1). Функции ЛИНЕЙН и ЛГРФПРИБЛ имеют одинаковые аргументы (табл. 2).
Таблица 1
Специальные функции MS Excel для нахождения аппроксимирующих функций, зависящих от нескольких переменных
|
Название функций |
Назначение |
|
ЛИНЕЙН |
Аппроксимация совокупности заданных точек x1, x2,..., xn линейной функцией вида y = a0 + a1x1 + a2x2 + ...+ anxn с применением метода наименьших квадратов. Позволяет найти неизвестные коэффициенты a0, a1, a2,..., an; коэффициент детерминации (R2) и другие показатели |
|
ЛГРФПРИБЛ |
Аппроксимация совокупности заданных точек x1, x2,..., xn показательными функциями вида y = a0a1x1a2x2...anxn. Позволяет найти неизвестные коэффициенты a0, a1, a2,..., an; коэффициент детерминации (R2) и другие показатели |
Таблица 2
Аргументы функций ЛИНЕЙН и ЛГРФПРИБЛ
|
№ |
Параметр |
Значение |
|
1 |
<Известные_значения_y> |
Множество наблюдаемых значений y1, y2,..., yn |
|
2 |
<Известные_значения_х> |
Множество наблюдаемых значений x1, x2,..., xn |
|
3 |
<Конст> |
Логическое значение, которое указывает, требуется ли вычислять a0: – ЛОЖЬ, если a0 принимается равным нулю для функции ЛИНЕЙН (прямая должна проходить через начало координат) и 1 для функции ЛГРФПРИБЛ; – ИСТИНА, если a0 вычисляется обычным образом |
|
4 |
<Статистика> |
Логическая переменная, которая указывает, требуется или нет вернуть дополнительную статистику по регрессии. Если аргумент имеет значение ЛОЖЬ или опущен, то функция возвращает только найденные коэффициенты |
Функция ЛГРФПРИБЛ работает подобно функции ЛИНЕЙН. Различия между ними состоят лишь в том, что ЛИНЕЙН определяет параметры прямой линии, наилучшим образом аппроксимирующей исходные данные, а функция ЛГРФПРИБЛ – экспоненциальной кривой. Чем больше график экспериментальных данных напоминает экспоненциальную кривую, тем лучше вычисленная кривая будет аппроксимировать данные. Функция ЛГРФПРИБЛ, так же как функция ЛИНЕЙН, возвращает массив, который описывает зависимость между значениями, но функция ЛИНЕЙН подгоняет прямую линию к имеющимся данным, а ЛГРФПРИБЛ подгоняет экспоненциальную кривую.
Для прогнозирования исследуемых значений используются функции MS Excel ТЕНДЕНЦИЯ и РОСТ (табл. 3). Функция ТЕНДЕНЦИЯ рассчитывает прогнозные значения исследуемого показателя в соответствии с линейным трендом. Подобно функции ЛИНЕЙН она с помощью метода наименьших квадратов аппроксимирует прямой линией массивы известных значений y и известных значений x. Однако в отличие от функции ЛИНЕЙН она определяет точки, лежащие на этой линии, и прогнозирует значения y для вновь заданных значений x [4]. При этом функция ТЕНДЕНЦИЯ не приводит математического описания и статистических характеристик самой модели тренда. Функции ТЕНДЕНЦИЯ и РОСТ имеют одинаковые аргументы (табл. 4).
Таблица 3
Специальные функции MS Excel для нахождения значений в произвольных точках на базе экспериментальных значений
|
Название функций |
Назначение |
|
ТЕНДЕНЦИЯ |
Позволяет находить значения полученной линейной функции y в произвольных точках, принадлежащих заданному интервалу |
|
РОСТ |
Используется для предсказания будущих значений y. Позволяет находить значения полученной показательной функции y в произвольных точках, принадлежащих заданному интервалу. Рассчитывает прогнозируемый экспоненциальный рост на основании имеющихся данных. Возвращает значения y для последовательности новых значений x, задаваемых с помощью существующих x- и y-значений |
Таблица 4
Аргументы функций ТЕНДЕНЦИЯ и РОСТ
|
№ |
Параметр |
Значение |
|
1 |
<Известные_значения_у> |
Множество наблюдаемых значений y1, y2,..., yn |
|
2 |
<Известные_значения_х> |
Множество наблюдаемых значений x1, x2,..., xn |
|
3 |
<Новые_значения_х> |
Значения х, для которых необходимо определить соответствующие аппроксимирующие или предсказанные значения у |
|
4 |
<Конст> |
Логическая переменная, принимающая значение: - ЛОЖЬ, если a0 принимается равным 0 при аппроксимации прямой и 1 – при аппроксимации показательной функцией; - ИСТИНА, если a0 вычисляется обычным образом |
Если аргумент <Новые_значения_x> опущен, то предполагается, что его значения совпадают со значениями аргумента <Известные_значения_x>. Эти функции, если не задавать аргумент <Новые_значения_x>, возвращают массив вычисленных значений y для фактических значений x в соответствии с прямой или кривой. Прежде чем использовать функцию ТЕНДЕНЦИЯ можно сначала рассчитать значения y по линейному тренду, а для функции РОСТ – значения y по экспоненциальному тренду.
Использование специальных проблемно-ориентированных статистических функций табличного процессора MS Excel позволяет выполнять обработку данных, полученных в ходе проведения эксперимента. Однако если задачи аппроксимации экспериментальных данных необходимо реализовать в составе «большого проекта» на языке программирования VB.NET, то в этом случае возникает необходимость знания алгоритмов и непосредственного программирования соответствующих методов. Возможности проектов, разрабатываемых в интегрированной среде визуального событийного объектно-ориентированного программирования VB.NET, можно существенно расширить за счет использования функций других пакетов, в частности, функций табличного процессора MS Excel [5].
Метод интеграции функций MS Excel в проекты VB.NET предусматривает создание в проекте ссылки на библиотеку объектов MS Excel помощью команды «Add Reference» меню «Project» (рис. 1).
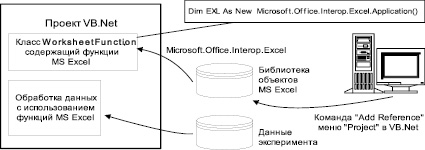
Рис. 1. Подключение и использование библиотеки объектов MS Excel в проекте VB.NET
В открывшемся диалоговом окне, во вкладке .Net, следует выбрать Microsoft.Office.Interop.Excel соответствующей версии. Далее необходимо создать экземпляр класса Excel.Application:
Dim EXL As New Microsoft.Office.Interop.Excel.Application()
После этого становится доступен класс WorksheetFunction, который и содержит все используемые в MS Excel функции [6].
Результаты исследования и их обсуждение
Рассмотрим пример практического использования функций табличного процессора MS Excel, предназначенных для анализа экспериментальных данных, полученных в результате следующего эксперимента [7]. Пусть в жидкость помещен источник радиоактивного излучения. На расстоянии 20, 50 и 100 см от источника расположены датчики. В качестве эксперимента проводились измерения интенсивности излучения через 1, 5 и 10 суток (табл. 5).
Таблица 5
Результаты экспериментального исследования
|
Расстояние до источника X1, см |
20 |
50 |
100 |
20 |
50 |
100 |
20 |
50 |
100 |
|
Периодичность измерения X2, сутки |
1 |
1 |
1 |
5 |
5 |
5 |
10 |
10 |
10 |
|
Интенсивность излучения Y, МРн |
61,2 |
33,6 |
12,3 |
43,6 |
24 |
8,8 |
28,3 |
15,6 |
5,7 |
Таблица 6
Задача обработки экспериментальных данных
|
Расстояние до источника X1, см |
0 |
0 |
0 |
200 |
200 |
200 |
|
Периодичность измерения X2, сутки |
0 |
1 |
3 |
0 |
1 |
3 |
|
Интенсивность излучения Y, МРн |
? |
? |
? |
? |
? |
? |
Таблица 7
Параметры метода WorksheetFunction.LogEst
|
Параметр |
Назначение параметра |
|
arg1 |
множество наблюдаемых значений Y, полученных в результате эксперимента |
|
arg2 |
множество значений X1, X2, для которых проводился эксперимент |
|
arg3 |
логическое значение: 1 – коэффициент a0 вычисляется обычным образом, 0 – устанавливается принудительно равным 1 |
|
arg4 |
логическая переменная: 1 – функция возвращает дополнительную информацию по регрессии, 0 – функция возвращает только коэффициенты регрессии. |
Таблица 8
Параметры метода WorksheetFunction.Growth
|
Параметр |
Назначение параметра |
|
arg1 |
множество наблюдаемых значений Y, полученных в результате эксперимента |
|
arg2 |
множество значений X1, X2, для которых проводился эксперимент |
|
arg3 |
множество значений X1, X2, для которых необходимо определить соответствующие аппроксимирующие или предсказанные значения Y |
|
arg4 |
логическая переменная: 1 – коэффициент a0 вычисляется обычным образом, 0 – устанавливается принудительно равным 1 |
После окончания эксперимента возникла необходимость определить интенсивность излучения возле источника, на расстоянии 200 см, в момент установки источника, через одни сутки и через трое суток (табл. 6).
Для решения данной задачи аппроксимируем совокупность заданных точек показательной функцией, зависящей от двух переменных вида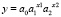 
. Затем сделаем прогноз для тех значений x1 и x2, которые в эксперимент не вошли. Для решения такой задачи в MS Excel используются функция ЛГРФПРИБЛ, позволяющая найти неизвестные коэффициенты a0, a1, a2 и коэффициент детерминации (R2), и функция РОСТ, рассчитывающая прогнозируемые значения функции в произвольных точках на базе экспериментальных данных.
Аналогом функции MS Excel ЛГРФПРИБЛ в VB.NET является метод класса WorksheetFunction.LogEst (табл. 7), а аналогом функции РОСТ в VB.NET – метод WorksheetFunction.Growth (табл. 8).
Результаты работы методов помещаются в соответствующие объекты, к которым можно обращаться так же как к элементам двумерного массива. Для описанного эксперимента это матрицы размерностью 5×3. Фрагмент программного кода, написанный на VB.NET в Visual Studio 2008 представлен на рис. 2.
Рис. 2. Фрагмент программного кода на VB.NET
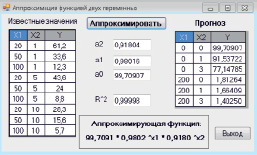
Рис. 3. Результат работы программного кода
Объект LPR(,) содержит результаты работы функции LogEst: значения коэффициентов a2, a1 и a0 помещаются в первую строку, стандартные ошибки для коэффициентов a2, a1, a0 – во вторую строку. В первый столбец третьей строки помещается коэффициент детерминации R2: если R2 >= 0,95, то имеет место высокая точность корреляции с моделью, если коэффициент R2 < 0,6, то уравнение регрессии неудачно и следует выбрать другой вид аппроксимирующей функции. Во второй столбец третьей строки помещается стандартная ошибка. В четвертую строку – значение критерия Фишера (1 столбец) и число степеней свободы (2 столбец). В пятую строку – сумма квадратов регрессии (1 столбец) и остаточная сумма квадратов (2 столбец). Объект Rost(,) содержит результаты работы функции Growth. Его первый столбец – это и есть рассчитанный прогноз. Результат работы программы приведен на рис. 3. Искомая аппроксимирующая функция имеет вид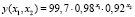 
, точность аппроксимации очень высокая: R2 = 0,99998.
Точно так же можно аппроксимировать экспериментальные данные для n независимых переменных показательной функцией вида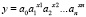 
. В этом случае объект LPR будет иметь размерность 5×(n + 1), его первая строка будет содержать коэффициенты 
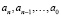. Аналогичным образом можно подключить другие функции MS Excel. Необходимо только знать англоязычный аналог их русифицированного названия, способ передачи параметров функции и как обработать объект, в котором содержится результат ее работы.
Заключение
Решение задачи обработки экспериментальных данных в проектах VB.NET на основе парадигм императивного и аспектно-ориентированного программирования подразумевает разработку алгоритмов и написание исходного кода подпрограмм для реализации соответствующих методов. Описанный метод интеграции функций табличного процессора MS Excel в проекты VB.NET для реализации анализа экспериментальных данных позволяет исключить непосредственное программирование алгоритмов их обработки. Таким образом, метод позволяет снизить затраты на разработку проектов VB.NET и исключить возможные ошибки, которые могли быть допущены при разработке процедур обработки данных.
Библиографическая ссылка
Карчевская М.П., Рамбургер О.Л., Тархов С.В. АНАЛИЗ ЭКСПЕРИМЕНТАЛЬНЫХ ДАННЫХ В ПРОЕКТАХ VB.NET С ИСПОЛЬЗОВАНИЕМ СПЕЦИАЛЬНЫХ ФУНКЦИЙ ТАБЛИЧНОГО ПРОЦЕССОРА MS EXCEL // Современные наукоемкие технологии. – 2019. – № 1. – С. 63-68;URL: https://top-technologies.ru/ru/article/view?id=37380 (дата обращения: 16.04.2024).