В настоящее время методы цифровой обработки сигналов (ЦОС) находят новые сферы своего применения. Так как алгоритмы ЦОС обладают достаточно высокой вычислительной сложностью, то для обеспечения обработки сигналов в режиме реального времени используются спецпроцессоры (СП). Среди методов цифровой обработки сигналов особое место принадлежит ортогональным преобразованиям сигналов, которые используют дискретное преобразование Фурье (ДПФ) и его быстрые алгоритмы. Наиболее наглядно это проявляется в беспроводных системах передачи данных, использующих технологию OFDM. Основными недостатками дискретных преобразований Фурье (ДПФ) с точки зрения цифровой обработки сигналов являются ошибки, возникающие вследствие округления или усечения результатов операций до используемой специализированными процессорами длины слова и наличие двух вычислительных трактов [1, 2]. Причем в конечных полях и кольцах может быть определено преобразование, аналогичное ДПФ и лишенное указанных недостатков [3]. Поэтому разработка алгоритмов ЦОС, использующих преимущества целочисленной арифметики и позволяющих устранить отмеченные недостатки ДПФ, является актуальной задачей.
С точки зрения реализации СП преобразований сигналов на основе ДПФ существует проблема представления словами конечной длины поворачивающих коэффициентов, являющихся иррациональными числами [4, 5]. Одним из направлений решения данной проблемы является использование конечных полей или колец с целью замены операций над действительными числами операциями над целыми числами. В работах [1, 2] предлагается в качестве альтернативы ДПФ использовать теоретико-числовые преобразования (ТЧП). Однако реализация ТЧП характеризуется значительными временными затратами. Поэтому разработка методов реализации теоретико–числовых преобразований сигналов, позволяющих устранить данный недостаток, является актуальной задачей. В работе [6] предложено использовать систолический принцип организации вычислений для повышения скорости выполнения ТЧП и разработан чисто-систолический алгоритм вычисления ТЧП (ЧСМ ТЧП) сигналов. Дальнейшее снижение временных затрат на выполнение ДВП возможно за счет применения многоканальных систолических матриц (МСМ). Поэтому целью работы является повышение скорости выполнения ТЧП за счет разработки алгоритма, использующего параллельно-конвейерные методы на основе многоканальных систолических матриц.
Материалы и методы исследования
Систолический принцип организации вычислений является одним из направлений построения систем ЦОС. Ячейки систолических процессоров (процессорные элементы) имеют, как правило, простую структуру и работают параллельно, выполняя одинаковую для одинаковых типов ячеек базовую операцию. Результаты вычислений предыдущей ячейки являются входными данными для последующей, передача данных осуществляется по всем локальным связям, причем данные в систолическом процессоре обрабатываются по мере выполнения всей необходимой совокупности базовых операций.
В работе [6] рассмотрены чисто-систолические матрицы, реализующие вычисления ТЧП по схеме Горнера. В ходе проведенных исследований было установлено, что перенос подходов, используемых при построении чисто-систолических СП ДПФ из поля комплексных чисел в конечные поля Галуа GF(M) позволяет повысить скорость вычисления ТЧП в 2,5 раза по сравнению с классическим алгоритмом. Рассмотрим возможность использования подходов, применяемых при проектировании многоканальных систолических СП ДПФ для разработки алгоритмов вычисления ТЧП.
ТЧП определяется для последовательностей целых чисел Sk и xn,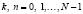 
, как пара преобразований:
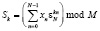, (1)
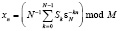, (2)
со структурой, похожей на структуру ДПФ. M, N – взаимно простые целые положительные числа, кроме этого, необходимым условием существования ТЧП является делимость Pi – 1 на N, где Pi – любой из простых сомножителей M, εN – такое число, что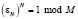 
и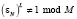 
, 
).
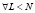В работе [4–1] показано, если εN является степенью двойки, то умножения в (1) и (2) можно осуществить сдвигами кодовых слов и приведением результата по модулю M.
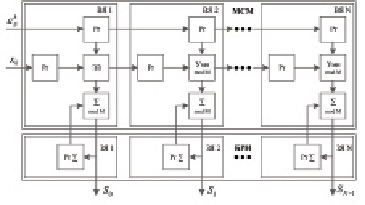
Рис. 1. Многоканальная систолическая матрица с блоком регистров-накопителей для вычисления ТЧП
Перенесем подходы, используемые при построении многоканальных систолических СП ДПФ из поля комплексных чисел в конечные кольца ZM и представим структуру многоканальной систолической матрицы (МСМ) с блоком регистров-накопителей (БРН) для вычисления ТЧП (МСМ ТЧП) на рис. 1. Ячейки БРН содержат накапливающий регистр Рr S, предназначенный для хранения промежуточных значений Sk. Каждая l-я ячейка (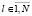
) МСМ ТЧП реализует вычисления Sk по формуле (1) следующим образом:
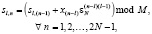(3)
где sl,n – значение накопленной суммы в n-й такт вычислений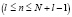 
в l-м регистре Рr S, 
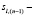то же на (n – 1) – такте, 
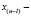значение отсчета исходных данных на n-м такте в l-й ячейке, 
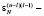значение степени (n – l) (l – 1) элемента порядка N, поступающего на вход l-ячейки в n-й такт.
Из формулы (3) видно, что вычисления sl,n осуществляются в независимых ячейках МСМ ТЧП, причем операции умножения и сложения разделены и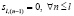 
. На рис. 2 представлена структура отдельной ячейки МСМ.
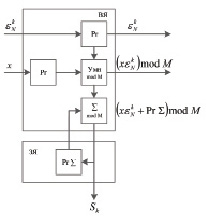
Рис. 2. Структура отдельной ячейки МСМ ТЧП
В каждый такт работы длительностью τ отдельная ячейка МСМ ТЧП (рис. 2) выполняет операции: п/п длительностью τ1 (передача на выход значения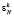 
, поступившего в ячейку на предыдущем такте; передача на выход результата предыдущего умножения; прием новых значений 
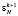и x), Умн mod M длительностью τ2 (умножение 
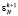на x по mod M), S mod M длительностью τ3 (суммирование результата умножения 
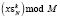с содержимым регистра Рr S), з/c длительностью τ4 (запись результата текущей суммы в Рr S, считывание результата суммирования в выходную шину на (N – 1 + l)-м такте и очистка Рr S l-й ячейки, 
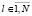) в соответствии с рис. 3.
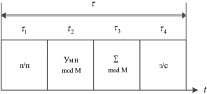
Рис. 3. Такт работы отдельной ячейки МСМ ТЧП
В соответствии с (1) при вычислении S0 отсутствуют операции умножения, поэтому первая ячейка МСМ ТЧП (рис. 1) является вырожденной, элемент задержки (ЭЗ) указанной ячейки синхронизирует микротакты передачи задержкой на время τ2 микротакта умножения. Временная диаграмма работы МСМ ТЧП при N = 5 представлена на рис. 4.
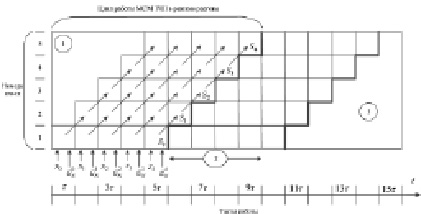
Рис. 4. Временная диаграмма работы МСМ ТЧП: 1 – начальный (холостой) ход при разгоне конвейера; 2 – обработка двух строк исходных данных в соседних циклах; 3 – холостой ход при торможении конвейера
Перед началом вычислений содержимое всех регистров Рr S равно нулю. На первом такте значения x0 и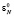 
загружаются в первую ячейку МСМ ТЧП. Через время τ1 + τ2 в соответствии с рис. 3 выполняется суммирование x0 с содержимым Рr S первой ячейки (на первом такте равным нулю) по модулю M. На микротакте τ4 результат суммирования (в нашем случае – x0), записывается в Рr S первой ячейки. На втором такте работы МСМ ТЧП (рис. 4) значения x0 и 
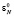передаются из первой ячейки во вторую, значения x1 и 
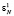загружаются в первую ячейку. На микротакте τ2 второго такта работы МСМ ТЧП – x1 задерживается в элементе задержки, во второй ячейке – x0 умножается на 
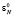по модулю M. Далее, на микротакте τ3 в первой и второй ячейках МСМ ТЧП выполняется суммирование по модулю M, результаты которого записываются в регистры Рr S первой и второй ячеек соответственно. Со второго такта первая и вторая ячейки работают синхронно (рис. 4).
На третьем такте работы МСМ ТЧП значения x0,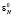 
загружаются в третью ячейку; x1 и 
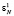– во вторую ячейку; x2 и 
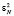– в первую. Далее ячейки l = 1, 2, 3 работают синхронно, на четвертом такте в работу включается четвертая ячейка и т.д. В соответствии с временной диаграммой работы МСМ ТЧП, на N-м такте параллельно работают все ячейки. В конце N-го такта, в результате выполненного первой ячейкой суммирования получается значение S0. На (N + 1)-м такте значение S1 будет сформировано во второй ячейке МСМ ТЧП, на (N + 2)-м, в третьей ячейке и т.д. Холостой ход при торможении конвейера выполняется в случае, если на (N + 1)-м такте в МСМ ТЧП не поступают новые данные. Если на (N + 1)-м такте в МСМ ТЧП поступают новые данные, то происходит совместная обработка двух строк исходных данных в такты с шестого по девятый. МСМ ТЧП переходит в установившийся режим работы, если, начиная с такта 2N, на обработку поступают новые данные. Таким образом, на рис. 4 можно выделить три режима работы МСМ ТЧП: разгон конвейера (первые N тактов); установившийся режим работы; торможение конвейера (последние (N – 1) тактов).
Приведем оценки характеристик вычислительного процесса МСМ ТЧП в установившемся режиме с учетом временной диаграммы работы (рис. 4):
– число тактов в каждом цикле вычислений
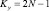; (4)
– число вычислительных тактов
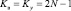; (5)
– число базовых операций, используемых для вычисления коэффициентов ТЧП
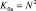; (6)
– производительность МСМ ТЧП в числе базовых операций
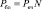, (7)
где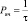 
– производительность одной ячейки (в числе базовых операций), τ = τ1 + τ2 + τ3 + τ4, τ – время выполнения базовой операции (рис. 3);
– производительность ЧСМ ТЧП для вычисления всего ТЧП по формуле (3)
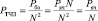; (8)
– время выполнения всего ТЧП в установившемся режиме
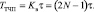(9)
Результаты исследования и их обсуждение
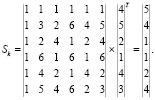
Рассмотрим пример реализации ТЧП по модулю М = 7. Для выполнения ТЧП на основе разработанного алгоритма потребуется 6 ячеек МСМ. В качестве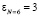 
. С помощью данного числа можно получить все ненулевые вычеты по модулю М = 7. В этом случае получаем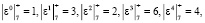 
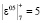. Пусть входной вектор имеет вид равный 
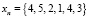. Согласно выражению (1) получаем
Рассмотрим работу МСМ, реализующей ТЧП по модулю М = 7. На первом такте работы на входы ячейки 1 МСМ подаются значения x0 = 4 и коэффициент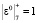 
, которые записываются в соответствующие регистры Рг. Затем значение x0 = 4 попадает на элемент задержки, а потом суммируется по модулю 7, предыдущим содержимым регистра РгS1. В результате в данный регистр записывается результат 
.
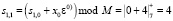На втором такте работы на входы ячейки 1 МСМ подаются значения x1 = 5 и коэффициент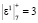 
, которые записываются в соответствующие регистры Рг. Затем число x1 = 5 подается на элемент задержки ЭЗ. А затем суммируется с содержимым регистра РгS1. В результате в данный регистр записывается результат 
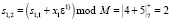. Одновременно с этими операциями из ячейки 1 в регистры Рг. ячейки 2 подаются значение 
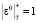и x0 = 4. Умножитель по модулю реализует операцию 
.
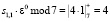Результат умножения подается на сумматор по модулю М = 7 второй ячейки, где выполняется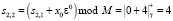 
. Результат записывается в регистр РгS2.
На третьем такте работы на входы ячейки 1 МСМ подаются значения x2 = 2 и коэффициент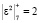 
, которые записываются в соответствующие регистры Рг. Затем число x2 = 2 подается на элемент задержки ЭЗ. А затем суммируется с содержимым регистра РгS1. В результате в данный регистр записывается результат 
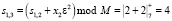. Одновременно с этими операциями из ячейки 1 в регистры Рг. второй ячейки подается значение 
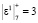и x1 = 5, а из ячейки 2 в регистры Рг. третьей ячейки подается значение 
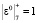и x0 = 4. Умножитель ячейки 2 реализует операцию 
.
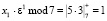Результат умножения подается на сумматор по модулю ячейки 2, где выполняется операция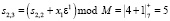 
. Результат суммы записывается в регистр РгS2. Умножитель третьей ячейки по модулю М = 7 реализует 
.
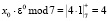Результат умножения подается на сумматор по модулю М = 7 третьей ячейки, где выполняется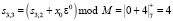 
. Результат записывается в регистр РгS3.
Дальше алгоритм выполняется подобным образом. Спустя 6 тактов с выхода первой ячейки МСМ будет выдаваться результат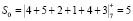 
. На следующих пяти тактах работы будут получены оставшиеся коэффициенты ТЧП 
.
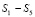Достоинствами МСМ ТЧП являются: 100 % использование оборудования. В работе [6] показано, что длительность вычисления в установившемся режиме равна TТЧП = 2Nτ. Для рассмотренного примера это составит TТЧП = 2Nτ = 12τ. При использовании МСМ для вычисления ТЧП потребуется TТЧП = (2N – 1)τ = 11τ. Таким образом, использование разработанного алгоритма вычисления ТЧП с использованием МСМ позволило повысить скорость вычисления в 1,09 раза по сравнению алгоритмом на основе ЧСМ и в более чем в 3 раза по сравнению с классическим алгоритмом ТЧП.
Заключение
Использование ТЧП вместо ДПФ в задачах ЦОС позволяет устранить ошибки округления результатов операций за счет перехода к целым числам, а также сократить один тракт. Разработанный алгоритм МСМ ТЧП, в отличие от ЧСМ ТЧП, может быть использован для параллельно-конвейерного расчета любого количества спектральных коэффициентов Sk,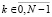 
. В ходе проведенных исследований показано, что использование разработанного алгоритма вычисления ТЧП с использованием МСМ позволило повысить скорость вычисления в 1,09 раза по сравнению алгоритмом ЧСМ и в более чем в 3 раза по сравнению с классическим алгоритмом ТЧП, в поле GF(7).
Исследование выполнено при финансовой поддержке РФФИ в рамках научного проекта № 18-37-00009.
Библиографическая ссылка
Калмыков М.И., Юрданов Д.В., Кононова Н.В., Калмыков И.А., Тынчеров К.Т. РАЗРАБОТКА МНОГОКАНАЛЬНОГО СИСТОЛИЧЕСКОГО АЛГОРИТМА ВЫЧИСЛЕНИЯ ТЕОРЕТИКО-ЧИСЛОВЫХ ПРЕОБРАЗОВАНИЙ СИГНАЛОВ В ПОЛЕ ГАЛУА GF(M) // Современные наукоемкие технологии. – 2019. – № 1. – С. 58-62;URL: https://top-technologies.ru/ru/article/view?id=37379 (дата обращения: 03.12.2024).