Обеспечение длительной прочности различных изделий и конструкций, работающих в условиях неизотермических процессов нагружения, продолжает оставаться актуальной задачей механики деформируемого твёрдого тела. Для оценки длительной прочности таких изделий на первом этапе расчёта необходимо максимально достоверно определить всю историю изменения их напряжённо-деформированного состояния с учётом возникающих упругих и пластических деформаций, развития деформаций ползучести и сопутствующей им деградации механических свойств материала. Тогда, располагая результатами расчёта напряжённо-деформированного состояния изделия, можно в первом приближении выявить опасные зоны и воспользоваться критериями длительной прочности по разрушению для оценки безопасного срока работы изделия [1]. Однако такой подход к оценке длительной прочности изделия, находящегося в условиях сложного и неоднородного напряжённого состояния, носит достаточно упрощённый характер. Для более точного определения долговечности изделия сложной формы в условиях сложного неоднородного напряжённого состояния необходимо использовать более общую постановку задачи, основанную на использовании континуальной механики разрушения, предложенной Ю.Н. Работновым [2, 3]. Этот подход предполагает введение в определяющие уравнения, описывающие напряжённо-деформированное состояние изделия, скалярного параметра повреждаемости материала при ползучести ωC. При этом для описания процессов накопления повреждения в материале используется кинетическое уравнение повреждаемости Ю.Н. Работнова [2]
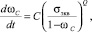(1)
где ωC – скалярный параметр повреждаемости; C и Q – параметры, зависящие от температуры и определяемые по кривым длительной прочности, полученным из испытаний на одноосное растяжение стандартных образцов при фиксированных значениях температуры; σэкв – эквивалентное напряжение, представляющее собой один из критериев длительной прочности.
Для описания истории изменения напряжённо-деформированного состояния изделия необходимо иметь информацию о механических свойствах материала, полученных в результате испытания стандартных образцов:
− на одноосное растяжение при различных фиксированных значениях температур с такой скоростью нагружения, при которой реологические свойства материала не проявляются, с построением на основе этих испытаний кривых мгновенного деформирования материала в пределах диапазона температур, при котором предполагается эксплуатация изделия;
− на ползучесть при различных фиксированных значениях напряжений и температур с построением соответствующих кривых ползучести и диаграмм длительной прочности.
Кроме того, необходимо экспериментальным или расчётным путём получить информацию об изменении температурного поля изделия в процессе его нагружения, а также иметь надёжные методы интерполяции и экстраполяции кривых ползучести и диаграмм длительной прочности по температуре и времени на периоды, соответствующие времени эксплуатации изделия [4, 5].
Как правило, такие задачи решаются численными методами, при этом процесс нагружения изделия разбивается на малые по времени этапы, а само изделие – на малые элементы, напряжённое состояние которых можно считать однородным. По этим данным необходимо для каждого этапа нагружения изделия определить характеристики напряжённо-деформированного состояния и степень повреждённости его элементов. И, таким образом, переходя от этапа к этапу, проследить историю деформирования изделия вплоть до его разрушения.
Цель исследования: анализ известных подходов к описанию обобщенного критерия длительной прочности Писаренко – Лебедева, используемого при определении эквивалентного напряжения, необходимого для описания процессов накопления повреждений в материале с помощью кинетического уравнения повреждаемости Ю.Н. Работнова, выбор способа его конкретизации и проверка достоверности результатов моделирования напряженно-деформированного состояния плоской пластины, получаемых при использовании данного критерия.
Материалы и методы исследования
Определению напряжённо-деформированного состояния изделий с учётом повреждаемости материала при ползучести посвящён целый ряд научных исследований. Некоторые из них приведены в работах [6–8]. При этом одним из важных и сложных вопросов является определение эквивалентных напряжений. Сложность этой задачи связана с большим количеством разработанных критериев длительной прочности и отсутствием чётких рекомендаций по их использованию. Наиболее обоснованным и универсальным, по мнению авторов, является обобщённый критерий длительной прочности Писаренко – Лебедева [9].
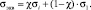(2)
Здесь σэкв – эквивалентное напряжение; χ – коэффициент пластичности материала, характеризующий степень ответственности за макроразрушение сдвиговой деформации, создающей благоприятные условия для разрушения материала и образования трещин [9], σi – интенсивность напряжений, которая при плоском напряженном состоянии определяется выражением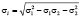 
, σ1 и σ2 – главные нормальные напряжения.
При оценке длительной прочности изделий и конструкций коэффициент χ может быть определён по результатам испытаний на длительную прочность сплошных цилиндрических образцов в условиях одноосного растяжения и сжатия, а также тонкостенных трубчатых образцов, подвергнутых испытанию на кручение. При этом вычисляются данные характеристики по формулам [9, 10]:
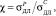(3)
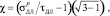(4)
где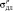 
, 
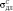, τДЛ – пределы длительной прочности при растяжении, сжатии и чистом сдвиге (кручении).
Проблемой применения данного критерия длительной прочности является отсутствие экспериментальных данных о длительной прочности материалов на сжатие и кручение.
В работах [8, 11] параметр χ является функцией интенсивности касательных напряжений и температуры и определяется из условии совпадения диаграмм длительной прочности при одноосном растяжении σ(t*) и чистом кручении τ(t*), при этом χ находится из выражения
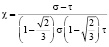, (5)
где напряжения σ и τ выбираются для одного и того же момента времени t*. Для заданного времени t* по диаграммам длительной прочности при растяжении и чистом кручении находятся соответствующие средние значения интенсивности касательных напряжений S. Эта процедура повторяется для различных значений при различных фиксированных температурах T. В результате строится зависимость χ = f(S, T), которая в дальнейшем используется при определении эквивалентного напряжения. Таким образом, данная методика предполагает проведение сложных и длительных испытаний на растяжение и чистое кручение трубчатых образцов, а это не всегда возможно.
Авторы работ [12–14] при использовании обобщённого критерия Писаренко – Лебедева параметр χ определяют как отношение длительной прочности материала на осевое растяжение и сжатие при фиксированном значении температуры. Ввиду больших методических трудностей проведения испытаний на осевое сжатие, характеристики ползучести и длительной прочности при этом виде нагружения в справочной литературе, как правило, отсутствуют. Поэтому и в данном случае становится практически невозможным использование обобщённого критерия длительной прочности.
Металлографические исследования, проведенные при испытании на ползучесть и длительную прочность некоторых металлов и сплавов, показывают, что в условиях высокотемпературной ползучести поликристаллических материалов имеют место три типа разрушения: внутризёренное, связанное со сдвиговыми деформациями в зернах, межзёренное, вызванное возникновением и развитием клиновидных трещин на стыках зёрен; межзёренное, связанное с образованием и развитием пор по границам зёрен [2]. Причём при высоких уровнях напряжений и высоких скоростях деформаций преобладает первый тип разрушения, определяемый уровнем действия касательных напряжений или интенсивности напряжений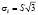 
. Второй и третий тип разрушения, объединённый одним общим названием межзёренное разрушение, проявляются при длительных воздействиях сравнительно малых напряжений и связаны с концентрацией напряжений по границам зёрен, а интенсивность их протекания зависит от уровня действующих нормальных напряжений. В реальных условиях в материале изделия в процессе ползучести имеют место все три типа разрушения, но в зависимости от величины нагрузки, продолжительности её действия, температуры преобладающим является тот или иной тип разрушения [13, 14]. По мнению авторов, с помощью критерия длительной прочности Писаренко – Лебедева можно учитывать изменение типов разрушения материала изделия, если параметр χ считать зависящим от уровня действующих напряжений, температуры и длительности развития деформаций ползучести.
В работе [15] авторами предложен простой и удобный для применения в расчётах вариант определения параметра χ при использовании обобщённого критерия прочности Писаренко – Лебедева, в соответствии с которым параметр χ для материала принимается равным относительному остаточному сужению при разрыве образца ψ. Подобный же подход предлагается использовать при определении параметра χ в расчётах на длительную прочность. Для этого введем новое обозначение этого параметра χC и будем предполагать, что χC = ψC, где ψC – относительное остаточное сужение сплошного круглого образца, полученное при его испытании на ползучесть и длительную прочность при постоянных значениях напряжения и температуры. Кроме того, как показывают испытания на ползучесть и длительную прочность стандартных цилиндрических образцов, изготовленных из металлов и сплавов, имеет место следующая закономерность: при высоких уровнях напряжений, существенно превышающих предел текучести материала, преобладает механизм внутризёренного разрушения (вязкое разрушение), сопровождающееся интенсивным развитием деформации ползучести, локализацией этой деформации и образованием шейки. При этом относительное остаточное сужение образца ψC, полученное при испытании на ползучесть, практически совпадает со значением относительного остаточного сужения ψ, полученного при стандартном испытании на растяжении сплошных цилиндрических образцов при их мгновенном деформировании до разрыва (ГОСТ 1497-84) при том же значении температуры. В то же время, при низких значениях напряжений, незначительно превышающих предел ползучести материала, преобладают межзёренные механизмы деформации и разрушения, наблюдается процесс интенсивного охрупчивания материала, образец деформируется равномерно по всей длине вплоть до разрушения без образования шейки, и разрушение происходит при малых значениях накопленной деформации ползучести, но за длительный период времени. При этом относительное остаточное сужение ψC будет принимать значения, близкие к нулю. Исходя из этих наблюдений и предполагая в первом приближении, что относительное остаточное сужение при ползучести образца, доведённого до разрушения, линейно зависит от уровня растягивающих напряжений, при которых происходят испытания, можно построить простую зависимость ψC = f(σ) для фиксированных значений температуры
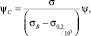(6)
где ψC – относительное остаточное сужение стандартного образца круглого поперечного сечения, полученное при испытании на ползучесть и длительную прочность при постоянном напряжении σ при заданной фиксированной температуре Т; ψ – относительное остаточное сужение, полученное при растяжении стандартного образца круглого поперечного сечения при его мгновенном деформировании при той же температуре; σB – предел прочности материала;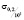 
– предел ползучести материала при заданной температуре.
Для использования полученного соотношения в расчётах на длительную прочность в справочной литературе имеются все необходимые данные для большинства конструкционных материалов [10]. На рис. 1 и 2 приведены графики зависимости относительного остаточного сужения при ползучести ψC от напряжения σ (сплошная линия), построенные по данной методике для стали 20 и для стали аустенитного класса 12Х18Н9Т. Кроме того, на графиках нанесены (темные кружки) значения ψC для этих же материалов, полученные экспериментальным путём для различных значений нормальных напряжений при тех же значениях температуры [10]. Анализ графиков показывает достаточно хорошее совпадение экспериментальных данных с предложенной методикой.
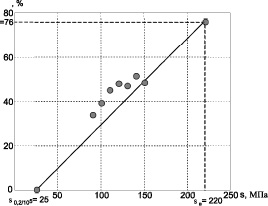
Рис. 1. Зависимость относительного остаточного сужения стали 20 при ползучести ψC от нормального напряжения при температуре 500 °С
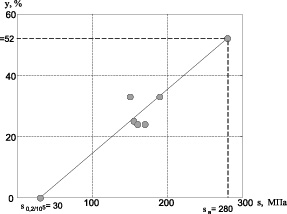
Рис. 2. Зависимость относительного остаточного сужения стали 12Х18Н9Т при ползучести ψC от нормального напряжения при температуре 650 °С
Таким образом, с использованием предложенного подхода эквивалентное напряжение для каждого элемента изделия на соответствующем этапе нагружения будет рассчитываться по формуле
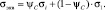(6)
Здесь ψC определяется в соответствии с соотношением (6). При этом в исходные данные для решения задачи дополнительно вводятся следующие механические характеристики материала для фиксированных значений температуры, соответствующих диапазону её изменения при эксплуатации изделия: предел прочности, предел ползучести и относительное остаточное сужение.
Результаты исследования и их обсуждение
С целью проверки адекватности предложенного способа конкретизации обобщённого критерия длительной прочности Писаренко – Лебедева были проведены проверочные расчеты равномерно нагретой до 500 °С однослойной кольцевой пластины с круглым отверстием, находящейся под давлением с верхней стороны (рис. 3). Пластина имеет следующие геометрические размеры: R = 110 мм, r = 65 мм, δ = 10 мм и изготовлена из материала сталь 20. Была проведена серия расчетов, в которых давление устанавливалось в диапазоне от 7 до 12 МПа, но при этом в каждом расчете оно было неизменным во времени.
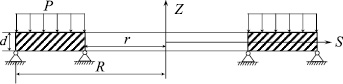
Рис. 3.
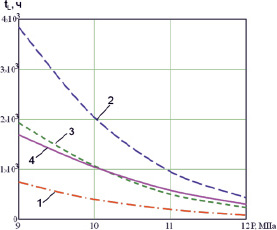
Рис. 4. Зависимость времени локального разрушения пластины от давления
Исследовалась зависимость времени до разрушения пластины от давления при использовании четырех различных критериев длительной прочности. Основные результаты расчетов приведены на рис. 4.
В качестве эквивалентного напряжения принимается (рис. 4):
1 – максимальное главное напряжение (критерий Джонсона): σЭ = σ1;
2 – интенсивность напряжений (критерий Каца):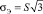 
;
3 – критерий Сдобырева: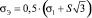 
;
4 – обобщённый критерий длительной прочности Писаренко – Лебедева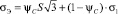 
.
На рис. 4 показаны кривые, отражающие зависимость времени до начала процесса разрушения пластины от давления в диапазоне от 9 до 12 МПа, при использовании четырех различных критериев длительной прочности.
Следует отметить, что использование критерия Джонсона дает минимальную оценку времени до разрушения конструкции (хрупкое разрушение), а критерия Каца – максимальную (пластическое разрушение) [14]. Таким образом, при использовании любого критерия длительной прочности диапазон значений времени до разрушения всегда будет лежать между значениями, полученными при использовании критериев Джонсона и Каца. Критерий Сдобырева является полусуммой этих двух критериев, и график, полученный с его применением, проходит почти посередине.
Анализируя полученные результаты, можно сделать вывод, что выбор критерия длительной прочности существенно влияет на оценку времени до разрушения конструкции, причем это влияние тем больше, чем меньше нагрузка и больше время нагружения конструкции. Предлагаемый вариант конкретизации обобщенного критерия Писаренко – Лебедева позволяет учитывать изменение пластических свойств материала (охрупчивание), которое происходит в процессе развития деформаций ползучести. На рисунке 4 видно, что кривые 3 (критерий Сдобырева) и 4 (обобщенный критерий Писаренко – Лебедева) проходят практически рядом, а при давлении 10,2 МПа – пересекаются. Значения напряжений, действующих в наиболее нагруженных точках пластины при данном давлении приблизительно равны 150 МПа, что соответствует значению ψ = 50 %. В дальнейшем кривая 4 приближается к кривой 2 (критерий Каца), что соответствует преобладанию вязкого типа разрушения над хрупким. При более низких давлениях критерий Писаренко – Лебедева показывает результаты, близкие к критерию Джонсона. Так, при значении давления 7 МПа критерий Джонсона показал значения времени до разрушения 10000 ч, критерий Каца – 70000 ч, а обобщенный критерий Писаренко – Лебедева – 12500 ч. Анализ уровня действующих напряжений в наиболее нагруженных точках показал, что они не достигают предела текучести, что в свою очередь указывает на преобладание хрупкого типа разрушения над вязким. При этом разница во времени до разрушения при давлении 7 МПа для критериев Джонсона и Каца оказывается весьма значительной и составляет порядка 60000 ч или различается в 7 раз. Поэтому их использование в неизменном виде приводит к получению недостоверного результата.
Заключение
Таким образом, предложенный в данной публикации способ конкретизации обобщенного критерия длительной прочности Писаренко – Лебедева в первом приближении позволяет учесть изменение пластических свойств материала в зависимости от времени нагружения, температуры и уровня действующих напряжений, что дает возможность учитывать преобладание различных типов разрушения (вязкое или хрупкое) и тем самым более точно рассчитать степень поврежденности материала и время до его разрушения. Для более детальной проверки адекватности данного критерия и способа его конкретизации требуются дополнительные исследования на основе данных, полученных в результате натурных экспериментов, некоторые из которых были представлены ранее в работе [13]. В дальнейшем авторы планируют провести эти исследования.
Библиографическая ссылка
Белов А.В., Неумоина Н.Г., Поливанов А.А. О ВЫБОРЕ КРИТЕРИЯ ПРОЧНОСТИ В РАСЧЕТАХ НА ДЛИТЕЛЬНУЮ ПРОЧНОСТЬ ПРИ НЕИЗОТЕРМИЧЕСКИХ ПРОЦЕССАХ НАГРУЖЕНИЯ // Современные наукоемкие технологии. – 2019. – № 1. – С. 20-25;URL: https://top-technologies.ru/ru/article/view?id=37372 (дата обращения: 21.11.2024).