Моделированием эмоций роботов в РФ начали заниматься относительно недавно. Однa из первых научных публикации по этой теме появилась в РФ в середине 1960-х гг. [1], но эта работа была посвящена математизации так называемых одиночных эмоций человека. В работе [2] описаны модели амбивалентных эмоций роботов. И лишь в 2016 г. сделана первая попытка математической формализации комплексных эмоций [3] роботов, при этом предполагалось, что комплексные эмоции роботов определяются вектором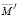 
, который имеет вид
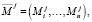(1)
где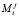 
– базовая эмоция робота, аналогичная базовой эмоции человека [4], n – количество базовых эмоций в комплексной эмоции робота, j – порядковый номер такта [5]. Отметим, что для представления комплексной эмоции в виде (1) вводится допущение о том, что все базовые эмоции имеют единую шкалу измерения.
Настоящая статья посвящена построению и исследованию моделей комплексных эмоций и воспитаний робота.
Комплексная эмоция робота с точки зрения векторной алгебры
Вектор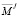 
можно расписать в виде суммы векторов:
,
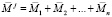где
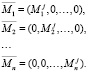
Очевидно, что в пространстве таких векторов существует базис
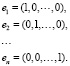
Таким образом, справедливо равенство
,
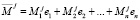и для комплексных эмоций робота выполняются правила векторной алгебры [6].
Будем предполагать, что базовые эмоции роботов удовлетворяют соотношениям
,
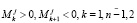где k – нечетные целые числа.
Приведенные выше неравенства можно описать формулой
.
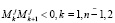Таким образом, можно сделать вывод о том, что количество компонент в комплексной эмоции робота всегда равно четному числу. Нетрудно заметить, что комплексные эмоции являются вектором амбивалентных эмоций робота [3], расположенных друг за другом в записи комплексной эмоции робота.
Комплексное воспитание робота
Будем предполагать, что у робота в ответ на любой раздражитель-стимул-сюжет возникает комплексная эмоция. Будем считать, что комплексная эмоция робота порождает его комплексное воспитание
,
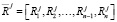где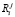 
– воспитание робота, получаемое в результате действия эмоции с порядковым номером i на такте j. Согласно введенному выше правилу эмоции с нечетным индексом положительные, с четным – отрицательные.
Согласно работе [5] воспитание робота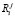 
представляется в виде
,
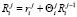где j – порядковый номер такта; tj-1, tj – время начала и конца такта j соответственно;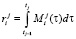 
элементарное воспитание робота, полученное на такте j, 
; 
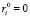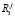– воспитание полученное роботом за время действия эмоции на такте j; 
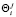– коэффициент памяти робота [5].
Ступоры робота по комплексным эмоциям
Согласно работе [5] cтупором называется состояние неопределенности робота при эмоциональном выборе. В работах [5, 7] предложены математические модели ступоров для некомплексных воспитаний робота R1 и R2, при этом ступор описывается единственным образом с помощью следующего соотношения:
.
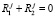Очевидно, что для комплексных воспитаний можно классифицировать все ступоры следующим образом:
1. Парный ступор.
2. Локальный ступор.
3. Всеобщий ступор.
Рассмотрим математические модели каждого из этих видов ступора.
Парный ступор возникает тогда, когда существует хотя бы одно такое нечетное значение величины i, что справедливо равенство
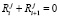. (2)
Локальный ступор – это ступор, при котором существует несколько таких нечетных значений величины i, что для этих значений справедливы соотношения (2).
Очевидно, что несколько парных ступоров могут породить локальный ступор.
Теорема 1. Если существует локальный ступор для воспитаний с нечетными номерами i и k, то сумма воспитаний с этими номерами и номерами i + 1, k + 1 равна нулю.
Доказательство. Так как согласно условию теоремы 1 справедливы соотношения
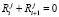, (3)
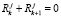, (4)
то, суммируя равенства (3) и (4), получим формулу
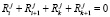, (5)
где k ≠ i, i, k – нечетные.
Соотношение (5) доказывает теорему 1.
Всеобщим ступором назовем такой ступор, при котором для всех нечетных величин i справедливы равенства
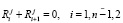. (6)
Теорема 2. Если наблюдается всеобщий ступор, то сумма всех компонент комплексного воспитания равна нулю.
Доказательство. В силу условия теоремы 2 справедливы соотношения (6), суммируя которые получаем формулу
, 
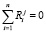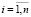. (7)
Очевидно, что равенство (7) доказывает теорему 2.
Для компьютерной реализации определения вида ступоров в комплексном воспитании можно предложить следующий простой алгоритм:
1. Комплексное воспитание разбивается на компоненты, являющиеся соседними ненулевыми парами, таким образом, чтобы минимальный порядковый номер компоненты, начиная с единицы, был нечетным.
2. Суммируются воспитания каждой пары.
3. Определяются номера тех пар, чье суммарное воспитание равно нулю.
4. Выводятся на печать пары с нулевой суммой воспитаний.
5. Делается вывод: Если количество таких пар равно 1, то присутствует парный ступор; если количество пар больше 1, но меньше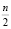 
, то присутствует локальный ступор; если количество пар равно 
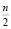, то присутствует всеобщий ступор.
6. Конец.
Парный ступор равномерно забывчивых роботов с равноценными эмоциями
Таким образом, теорема 1 и теорема 2 формулируют необходимые условия для локального и всеобщего ступоров соответственно.
В работе [5] для равноценных эмоций равномерно забывчивых роботов доказана теорема о том, что существуют антиступорные коэффициенты памяти [8], то есть такие коэффициенты, при которых у робота никогда не наступит ступор. Обобщая работу [5] для комплексных воспитаний, можно сказать, что такими коэффициентами памяти являются, например, следующие числа – для воспитаний с нечетным номером i – коэффициент памяти, равный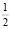 
при одновременном равенстве 
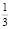коэффициента памяти у воспитаний с номером i + 1 или наоборот.
Рассмотрим равномерно забывчивых роботов с парными одинаковыми по моделю равноценными эмоциями. Пусть рассматриваемая пара компонент-воспитаний комплексного воспитания имеет номера i и i + 1. Тогда по определению равномерно забывчивых роботов с равноценными эмоциями [5] справедливы соотношения
, 
,
, 
.
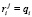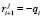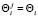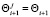Вставляя эти обозначения в условие парного ступора, получим цепочку равенств:
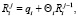
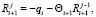
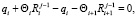
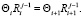(8)
Так как при введенных допущениях моделей равномерно забывчивые роботы имеют равноценные эмоции, то справедливы соотношения [5]:
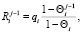
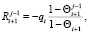
из которых для описания ступора согласно формуле (8) следует равенство
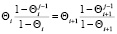. (9)
В силу определения ступора справедливо равенство
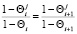. (10)
Численные эксперименты, проведенные на основе решения системы уравнений (9)–(10) при заданных величинах j, меняющихся согласно правилу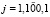 
, показывают, что решением уравнений (9)–(10) являются любые коэффициенты памяти, удовлетворяющие равенству 
.
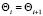Таким образом, выполненные численные эксперименты позволяют выдвинуть гипотезу о том, что парный ступор для равномерно забывчивых роботов с равноценными эмоциями возможен только при равенстве коэффициентов памяти парных комплексных эмоций робота.
В работе [5] введено понятие антиступорных коэффициентов памяти, т.е. коэффициентов, при которых ни при каком значении j не являются справедливыми равенства (9) и (10).
Согласно выполненным численным экспериментам можно выдвинуть гипотезу о том, что для равномерно забывчивых роботов с парными равноценными комплексными эмоциями все коэффициенты памяти, кроме равных друг другу, являются антиступорными коэффициентами памяти.
Предположим, что парный ступор возникает при предельном воспитании [5] робота. В этом случает равенство (10), описывающее парный ступор, примет вид
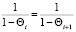. (11)
Нетрудно заметить, что соотношение (11) влечет формулу
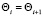. (12)
Очевидно, что при справедливости равенства (12) всегда справедливо соотношение (9). Это позволяет сформулировать теорему 3:
Для равномерно забывчивых роботов с равноценными эмоциями для парного ступора предельных воспитаний необходимо и достаточно равенство коэффициентов памяти парных компонент комплексных эмоций робота.
Заключение
Таким образом, в настоящей статье предложена математическая модель комплексных эмоций и комплексных воспитаний робота, а также представление этих эмоций через базовые эмоции робота, приведены и доказаны условия возникновения ступоров при комплексных эмоциях робота. Предложенные модели могут использоваться как при анализе «психоэмоционального» состояния роботов, так и при проектировании эмоциональных роботов с заданными «психологическими» характеристиками.
Библиографическая ссылка
Пенский О.Г., Анисимова С.И. МАТЕМАТИЧЕСКИЕ МОДЕЛИ КОМПЛЕКСНЫХ ЭМОЦИЙ И КОМПЛЕКСНЫХ ВОСПИТАНИЙ РОБОТА // Современные наукоемкие технологии. – 2018. – № 12-2. – С. 343-346;URL: https://top-technologies.ru/ru/article/view?id=37344 (дата обращения: 27.12.2024).