Согласно материалам публичных аналитических докладов Сколковского Института Науки и Технологий 2014–2015 гг. [1, 2] основное внимание в ведущих промышленных странах уделяется нескольким направлениям научных исследований в интересах совершенствования производства: CAD/САМ/CAE технологии компьютерного проектирования сложных технических систем и процессов, робототехника, аддитивные технологии, композиционные материалы с иерархической структурой. При этом можно сделать вывод, что последние два направления тесно взаимосвязаны, поскольку наиболее эффективным методом формирования иерархической структуры материалов в условиях многономенклатурного производства, согласно разнообразным требованиям заказчиков, является послойное нанесение моно- или поликомпонентных составов (аддитивные процессы). При этом большое внимание уделяется качеству материалов.
За последние 20 лет объем применения композиционных, в том числе керамических, материалов в аэрокосмической технике увеличился более чем в два раза и данная динамика продолжает усиливаться [3–5]. В перспективе ожидается расширенное применение полимерных композиционных материалов (ПКМ) в ракетно-космической технике. Эта мировая тенденция характерна и для российской космической промышленности. В России разрабатывается и создается новое поколение космических аппаратов, в которых может быть заметно увеличена доля и роль композиционных и керамических материалов: перспективная экранновакуумная теплоизоляция с функцией микрометеороидной защиты для «Научно-энергетического модуля» МКС, лобовой теплозащитный экран для многоразового пилотируемого космического корабля «Федерация» и др. Планирующееся возобновление работ по исследованию и освоению Луны, в том числе с созданием на ее поверхности долговременных обитаемых модулей, также предполагает применение композиционных материалов со специальными функциональными свойствами.
При этом направления исследований в области материаловедения для космических аппаратов определяются спецификой долговременного нахождения данных объектов в открытом космическом пространстве под действием высоких градиентов температур, ионизирующих излучений, корпускулярных потоков и динамических нагрузок вследствие столкновений с микрометеоритами и «космическим мусором». В ходе исследований, выполненных космонавтами и астронавтами на долговременных космических станциях («Салют», «Скайлэб», «Мир», МКС), выявлены следующие основные факторы, влияющие на прочность и надежность конструкций из композиционных материалов: микроэрозионное повреждение поверхности и доотверждение связующего. При этом глубина повреждений и степень доотверждения зависят от состава и структуры материала, технологии его изготовления, исходной степени отверждения, максимальной температуры термоциклов и продолжительности экспонирования. Из-за температурного градиента по толщине образцов в процессе экспонирования формируется градиент физико-механических показателей ПКМ по толщине пластины. Вследствие упрочнения слоев гибридных композитов под воздействием термоциклов изменяется характер разрушения при изгибном нагружении [6]. Исследование поведения конструкций из ПКМ в космосе выявило особую важность их термостабильности в интервале температур 100…450 K в условиях периодических теплосмен, вызванных движением через теневые участки орбиты. Термостабильные конструкции создаются применением ПКМ с малыми значениями коэффициента линейного термического расширения (КЛТР) и высокой теплопроводностью. Считается [7], что для этой цели наилучшим образом подходят углепластики при условии значительного увеличения их теплопроводности в направлении больших ожидаемых температурных градиентов. Однако проблема создания теплопроводных композитных конструкций осложнена тем, что действительные физико-механические свойства ПКМ можно определить лишь после изготовления конкретной детали, т.е. в отвержденном состоянии. Кроме того, ПКМ отличаются значительной анизотропией физико-механических и теплофизических свойств, определяемой как схемами армирования, так и различием на порядок и более данных свойств для матрицы и наполнителя [8, 9]. Часто высокие физико-механические характеристики ПКМ слабо коррелируют с его теплофизическими свойствами, что создает трудности при разработке внешних конструкций как космических аппаратов, так и инженерных сооружений, предназначенных для эксплуатации в условиях Крайнего Севера, Антарктиды и высокогорья.
На основании изложенного, разработка методов регулирования теплофизических свойств полимерных композиционных материалов применительно к заданным условиям эксплуатации при сохранении высоких прочностных характеристик представляет собой актуальную научную и практическую задачу.
Для расчета эффективной термической проводимости элементарной периодической ячейки применяется метод гомогенизации, в котором гомогенизированные выражения могут быть получены из уравнений теплопроводности. По [10, 11] эффективная теплопроводность может быть определена в следующей форме:
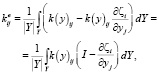(1)
с локальной координатой y.
Если обозначить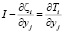 
[11], то, аналогично схеме, используемой для интерполяции локального тензора жесткости, характеристическая функция Ti – является решением уравнения теплопроводности:
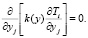(2)
Тогда эффективный тензор теплопроводности (1) может быть записан в виде
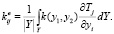(3)
Для двумерной ячейки тензор эффективной термической проводимости представляется как
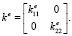(4)
Таким образом, для измерения общей эффективной проводимости материала может служить выражение
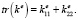(5)
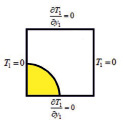
Граничные условия для определения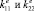 
приведены на рис. 1.
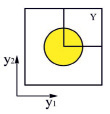
а) б) в)
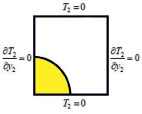
Рис. 1. Элементарная периодическая ячейка композита: а) область топологической оптимизации Y и граничные условия для задач теплопроводности (б), (в)
Граничные условия для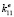 
:
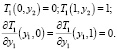
Граничные условия для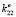 
:
Материалы и методы исследования
На сегодняшний день, метод гомогенизации [10] является эффективным подходом к вычислению глобальных физических свойств композита, таких как объемный модуль жесткости или термическая проводимость.
Определившись с упругой и термической гомогенизацией, представляется возможность поставить задачу оптимизации, которая позволит определить оптимальную топологию для сочетания упругой и термической задач. Такие задачи особенно интересны, когда упругие и термические свойства материалов сильно конкурируют друг с другом, и оптимальные топологии для отдельных задач оптимизации сильно отличаются друг от друга. Чтобы решить поставленную задачу, необходимо одновременно учитывать как упругие, так и термические свойства материала.
Предположим, что элементарная периодическая ячейка разбита на конечные элементы и каждому элементу присваивается переменная плотность, ρn(n = 1, N). Следуя закону SIMP [12], в котором в качестве переменной управления в задаче оптимизации выступает искусственно введённая плотность ρ(x), коэффициент теплопроводности:
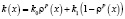. (6)
Здесь k0, k1 – коэффициенты термической проводимости материалов соответственно.
Показатель степени p ≥ 1 является фактором штрафа и увеличение р приводит к более четкому решению. Показатель степени p обычно выбирают равным p = 4 или p = 5 [12].
Обычно задачи оптимизации на максимум для удобства расчетов сводятся к задачам на минимум.
Целевую функцию определим в виде
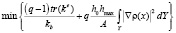. (7)
Здесь kb – коэффициент теплопроводности, используемый для нормировки. Второе слагаемое является функцией штрафа для исключения эффекта «шахматной доски» в процессе оптимизации, h0 первоначальный размер сетки и hmax – текущий размер сетки. Величина 0 ≤ q ≤ 1 – заданный коэффициент, позволяющий сбалансировать функцию цели и функцию штрафа друг с другом. Следует отметить, что поиск минимума функции (8) соответствует задаче поиска максимума функции, стоящей после множителя (q – 1) за счет того, что q – 1 ≤ 0 [13].
Ограничения для искусственно введенной плотности ρ(x) выберем в виде
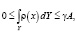(8)
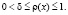(9)
В формуле (8) A обозначает общий объем материала оптимизируемой области Y в элементарной периодической ячейке при ρ(x) = 1 и γ обозначает процент экономии материала с параметрами.
Поскольку для получения численного решения жесткость не должна полностью исчезать, положим, в неравенстве (9) δ равной некоторой достаточно малой величине, чтобы избежать сингулярности начальной матрицы жесткости при оптимизации.
Результаты исследования и их обсуждение
Рассмотрим элементарную ячейку композита из двух материалов, коэффициенты термической проводимости которых соответственно равны k0 = 10, k1 = 100. Оптимальную микроструктуру композита будем строить для различных значений от γ = 0,2 до γ = 0,9, γ – объемная доля материала с коэффициентом теплопроводности k1 = 100.
Тогда коэффициент теплопроводности в произвольной точке микроструктуры определяется выражением
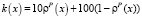. (10)
В таблице приведены оптимальные топологии, значения эффективной теплопроводности при различных значениях γ.
Эффективная теплопроводность композита в зависимости от доли компонента с повышенной теплопроводностью в общем объеме
|
γ |
0,2 |
0,3 |
0,4 |
0,5 |
|
|
|
|
|
|
|
tr(k)/2 |
19,9672 |
26,2511 |
33,2693 |
41,0807 |
|
γ |
0,6 |
0,7 |
0,8 |
0,9 |
|
|
|
|
|
|
|
tr(k)/2 |
49,8471 |
59,7396 |
70,202 |
84,2823 |
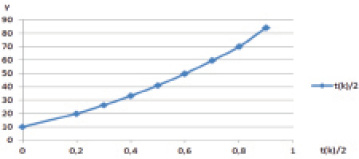
Рис. 2. Теоретическая зависимость теплопроводности ПКМ в зависимости от % % доли компонента с условной теплопроводностью γ = 100
Построенная по результатам моделирования зависимость представлена на рис. 2.
Анализ графика (рис. 2) позволяет сделать вывод, что введение в структуру основного материала дополнительного компонента с высокой теплопроводностью, распределенного с учетом рациональной топологии, позволяет существенно повысить данную теплофизическую характеристику. Например, размещение 20 % от общего объема дополнительного компонента приводит к увеличению теплопроводности в 2 раза, а замена 80 % материала на теплопроводный компонент вызывает семикратное увеличение теплопроводности. С учетом возможных различий в механических характеристиках компонентов использование топологического структурирования ПКМ материалом с отличающейся от основного теплопроводностью позволяет путем введения относительно малой его доли, не вызывающей значимого изменения механических характеристик, существенно изменить в требуемом направлении теплофизические свойства. Таким образом, появляется инструмент направленного регулирования теплофизических свойств ПКМ с учетом их прочности и других механических
свойств.
В то же время представленные выше результаты моделирования элементарных ячеек композиционного материала с внутренними структурами повышенной теплопроводности дают представление о высокой сложности формы данных структур, что требует оценки практической реализуемости предлагаемого подхода в серийной технологии.
В последнее время получают все большее распространение в различных областях производства аддитивные технологии прямого формирования трехмерных объектов любой сложности формы на основе разработанной компьютерной твердотельной модели [10–12]. Среди различных методов данного технологического направления технология FDM позволяет формировать композиционные изделия из различных полимерных материалов в соответствии с заданной структурой.
Ранее нами были получены положительные результаты по формированию упрочняющей топологии в виде армированного углеродными волокнами композита в объектах трехмерной печати путем выкладки армирующего материала в соответствии с полученным на основе компьютерного моделирования распределением полей напряжений. При этом полости для заполнения, имеющие сложную форму, были получены в процессе печати основы из пластика ABS [13]. Изучены теплофизические и механические свойства таких объектов, в том числе после дополнительного электрофизического воздействия [14, 15].
На основании изложенного представляется возможным предложить следующий алгоритм формирования структуры ПКМ с оптимизированными прочностными и теплофизическими характеристиками:
– на основе известных требований к изделию проектируется его конструкция;
– на основе конструкции формируется твердотельная модель изделия;
– с учетом распределения и расчетных численных эксплуатационных нагрузок моделируется распределение полей внутренних напряжений для последующего топологического упрочнения материалов с высокими модулем упругости и пределом выносливости и статической прочности;
– с учетом известных температурных градиентов и требуемой теплопроводности моделируется внутренняя структура из материала с высокой теплопроводностью;
– разрабатывается обобщенная твердотельная модель изделия, учитывающая упрочняющую топологию и распределение теплопроводных структур;
– подбираются соответствующие назначению основной конструкционный, упрочняющий материалы и материал с повышенной теплопроводностью;
– методом аддитивных технологий на основе многокомпонентной трехмерной печати формируется изделие.
Выводы
На основе математического и компьютерного моделирования получены топологии распределения дополнительного компонента с различным процентным содержанием в полимерном композиционном материале, позволяющие изменять его теплофизические характеристики, в частности теплопроводность.
Теоретически установлено, что в зависимости от доли содержания дополнительного компонента: (20–90) % условная теплопроводность композита повышается соответственно от 2 до 8 раз, что позволяет путем незначительных изменений содержания теплопроводного компонента в широких пределах направленно регулировать теплопроводность изделия из ПКМ.
Анализ современных технологий формирования изделий из полимерных и композиционных материалов позволяет сделать вывод о целесообразности применения технологий трехмерной печати для практической реализации рассмотренного в данной статье подхода. Применение данных технологий особенно важно с учетом имеющихся решений по топологической оптимизации прочностных характеристик полимерных композиционных материалов путем формирования в их объеме упрочняющих структур в соответствии с установленной закономерностью распределения полей напряжений от действия внешних нагрузок.
Сочетание упрочняющей и теплофизической оптимизации структуры ПКМ позволит сформировать заданный условиями эксплуатации объекта комплекс свойств, что особенно важно для динамичных объектов, находящихся в условиях высоких температурных градиентов, например, космических аппаратов, а также инженерных конструкций и транспортной техники для зон Крайнего Севера и Антарктиды.
Исследования выполнены при поддержке гранта РФФИ № 17-03-00720 «Методология оптимизационного микроконструирования композиционных материалов для объектов сложной формы повышенной динамической прочности, послойно формируемых электротехнологическими методами».
Библиографическая ссылка
Павлов С.П., Макарова В.М., Злобина И.В., Бекренев Н.В. ПРЕДПОСЫЛКИ РЕГУЛИРОВАНИЯ ТЕПЛОПРОВОДНОСТИ ПОЛИМЕРНЫХ КОМПОЗИЦИОННЫХ МАТЕРИАЛОВ НА ОСНОВЕ МОДЕЛИРОВАНИЯ ТЕПЛОВЫХ ПОТОКОВ И АДДИТИВНЫХ ТЕХНОЛОГИЙ // Современные наукоемкие технологии. – 2018. – № 12-2. – С. 337-342;URL: https://top-technologies.ru/ru/article/view?id=37343 (дата обращения: 26.12.2024).