В качестве армирующих наполнителей, при производстве деталей из полимерных композиционных материалов широкое распространение получили углеродные ткани, ленты и волокна [1, 2]. По своим удельным характеристикам они в десятки раз превышают алюминиевые и титановые сплавы. Области применения углепластиков с каждым годом постоянно расширяются, что связано с их уникальными механическими и теплофизическими характеристиками. Большое разнообразие углеродных волокнистых наполнителей и сложные эксплуатационные условия, при которых эксплуатируются композитные конструкции, приводят к необходимости совершенствования эксплуатационных характеристик существующих материалов, что порождает проблематику расширения комплекса их свойств [3–5].
Для модификации свойств углеродных тканей используются различные технологии: окисление, аппретирование, гальваническая обработка и др. Одним из методов регулирования свойств композитов на основе углеродных наполнителей является технология металлизации [6, 7].
В работах [8, 9] показано, что для регулирования свойств композитов на основе углеродных наполнителей также может быть использована технология металлизации, которую чаще всего проводят, используя такие металлы, как никель, железо, молибден, цирконий, алюминий и медь. Основной целью металлизации является изменение физико-химических свойств поверхности углеродных наполнителей, что позволяет регулировать их реакционную способность, биосовместимость и теплофизические свойства и др. Традиционным способом регулирования теплопроводности полимерных материалов является использование металлических порошкообразных наполнителей [10–12]. В настоящей работе вместо дисперсных теплопроводных наполнителей использовались углеродные ленты, на которые методом магнетронного распыления наносили различные металлические покрытия. Свойства металлизированных углеродных тканей и углепластиков на их основе исследуются экспериментальными методами, которые являются трудоемкими и дорогостоящими. Создание адекватных математических моделей позволит существенно сократить путь от идеи до опытно-конструкторского образца.
Целью настоящей работы является разработка математических моделей, позволяющих прогнозировать напряженно-деформированное состояние элементарных нитей с металлическим покрытием. Достоверность созданных моделей оценивали по результатам экспериментальных исследований путем проведения механических испытаний элементарных нитей до и после нанесения на углеродные ленты различных металлических покрытий.
Материалы и методы исследования
Задача создания математической модели элементарной углеродной нити, на поверхность которой нанесено тонкое металлическое покрытие, является актуальной, поскольку позволит моделировать поведение под нагрузкой самых различных систем. В настоящей работе рассматриваются углеродные ленты и ткани, однако даже для этого, казалось бы, ограниченного класса объектов, используются разные исходные материалы (на рис. 1 они названы – материальные объекты, в качестве которых могут быть использованы ПАН, пеки и др.).
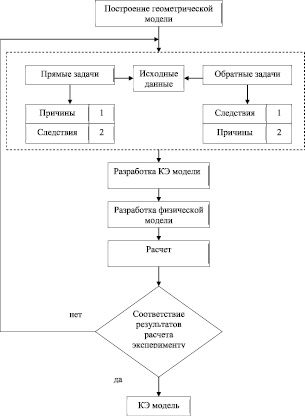
Рис. 1. Структура процесса решения прямых и обратных задач
Различные технологии производства также относятся к материальным объектам и различаются в зависимости от используемого оборудования, технологических режимов и т.д. В результате даже при условии использования в качестве исходного материала ПАН разные производители производят углеродные ткани и волокна, существенно различающихся между собой. Кроме внешней и внутренней технологических сред, на качество производимых волокон оказывает влияние рыночная конкуренция, которая среди производителей углеродных волокон очень велика, что во многом и заставляет их создавать собственные составы аппретов, технологии шлихтования и т.д. Таким образом, создание адекватных моделей позволит существенно сократить путь от идеи до НИР и ОКР.
Еще в большей степени, чем свойства углеродных волокон, произведенные различными производителями, различаются свойства материалов, используемых в качестве металлических покрытий и технологии их нанесения. Проведение экспериментальных исследований требует больших затрат времени и средств.
При проведении моделирования напряженно-деформированного состояния элементарной нити с металлическим покрытием в работе использован метод решения обратных задач. Отличительной особенностью решения обратных задач (по сравнению с прямыми задачами) являлась разница в причинно-следственных связях. К причинным характеристикам, как правило [13], относят начальные и граничные условия. К следственным характеристикам относятся условия нагружения (полный набор этих показателей называют полем физических величин. Структура причинно-следственных связей при решении прямых и обратных задач показана на рис. 1. При решении прямых задач по причинным характеристикам определяют следственные характеристики. При решении обратных задач – наоборот, по заданным следственным характеристикам находят причины.
В настоящей работе была поставлена задача определения значений перемещений при известных величинах разрушающей нагрузке. Такая постановка задача была связана с тем, что ранее [8, 9] экспериментально были найдены значения разрушающих напряжений и перемещений при заданных нагрузках. При решении прямых задач не ясно, будет ли происходить разрушение элементарных нитей при заданных величинах нагрузок. Такая неопределенность связана с тем, что нагрузки задаются случайным образом и в процессе моделирования полученные величины напряжений и перемещений могут быть сколь угодно большими. Если же решать обратную задачу (т.е. задавать такое значение нагрузки, при которой происходило разрушение исследуемого образца в процессе экспериментальных исследований), то появляется возможность сравнить ранее найденные значения перемещений (или же напряжений) с теми, что получены в результате расчетов.
Расчеты элементарной нити с покрытием проводили для металлических покрытий из нержавеющей стали и титана. Толщину покрытия изменяли от 50 до 200 нм. Модель элементарной углеродной нити (рис. 2) строили в программе SiemensNX, все расчеты проводили в программном комплексе NX/Nastran.
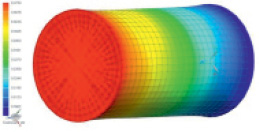
а)
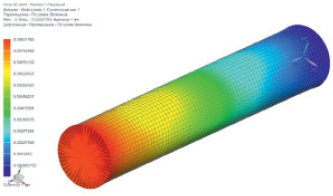
б)
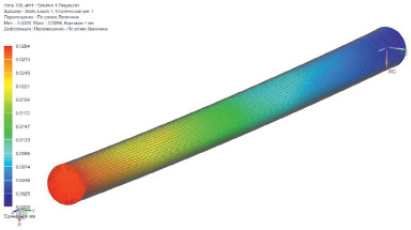
в)
Рис. 2. Результаты расчета перемещений элементарной нити, длиной 10 мм (а), 30 мм (б) и 100 мм (в)
Достоверность созданных моделей оценивали по результатам экспериментальных исследований элементарных нитей. В качестве объектов исследования в работе использованы две углеродные ленты ЛУП и Fibra. Для нанесения на них металлических покрытий использовали установку магнетронного распыления МИР-2. В качестве мишеней применяли: медь марки М1, цинк Ц2, титан ВТ1-0, нержавеющею сталь 12Х18Н10Т, алюминиевый сплав АМц и серебро 99,99.
Механические испытания элементарных нитей с различными типами металлических покрытий проводили на универсальной испытательной машине марки Zwick//Roell.
Результаты исследования и их обсуждение
В табл. 1 приведены результаты экспериментальных исследований прочности элементарных нитей до и после нанесения на углеродные ленты металлических покрытий.
Таблица 1
Свойства элементарных нитей до и после нанесения металлических покрытий
|
Материал покрытия |
Разрушающее напряжение, МПа |
Относительное удлинение при разрыве, % |
|
Углеродная лента ЛУП |
||
|
Без покрытий |
1773 |
0,78 |
|
Нержавеющая сталь |
1893 |
0,73 |
|
Титан |
1529 |
0,60 |
|
Медь |
1881 |
0,72 |
|
Цинк |
1397 |
0,59 |
|
Алюминий |
1260 |
0,74 |
|
Серебро |
1320 |
0,77 |
|
Углеродная лента Fibra |
||
|
Без покрытий |
3010 |
1,96 |
|
Нержавеющая сталь |
4640 |
1,88 |
|
Титан |
4360 |
1,84 |
|
Медь |
4430 |
1,95 |
|
Цинк |
2460 |
1,93 |
|
Алюминий |
2120 |
1,95 |
|
Серебро |
3810 |
1,94 |
Из полученных результатов экспериментальных исследований следует, что прочность элементарных нитей, в зависимости от типа наносимого металлического покрытия, может как увеличиваться, так и уменьшаться. Например, при нанесении на углеродную ленту ЛУП в качестве покрытия титана, цинка, алюминия и серебра имеет место снижение прочности элементарных нитей на 13,7; 15,6; 28,9 и 25,5 % соответственно. В то же время, при нанесении покрытия из нержавеющей стали и меди имеет место повышение прочности элементарных нитей на 6,7 % и 6 % соответственно. Для углеродной ленты Fibra металлические покрытия из нержавеющей стали, титана, меди и серебра приводят к повышению прочности элементарных нитей на 54, 44, 47 и 26 % соответственно, тогда как покрытия из цинка и алюминия, наоборот, ее уменьшают на 18 % и 30 % соответственно.
Для углеродных лент марок Луп и Fibra, независимо от нанесенного металлического покрытия, имеет место снижение деформационных характеристик элементарных нитей.
Теоретические оценки напряженно-деформированного состояния элементарных нитей проводили по величине перемещений. Первоначально была построена модель элементарной нити без покрытия. При построении геометрической модели полагали, что диаметр элементарной нити равен 10 мкм, ее длину варьировали от 10 до 100 мкм. Для модели нити был использован трехмерный тип сетки, размер конечного элемента составил 250 нм. К модели прикладывали нагрузку 200 сН в виде распределенной растягивающей силы. С противоположной стороны образца использовалась заделка. Результаты расчетов показаны в табл. 2 и частично на рис. 2. Значения длин элементарных нитей, на которых фиксировались значения перемещений, указанных в процентах в табл. 2, соответствует различным цветам, которыми показаны соответствующие значения перемещений по длине образцов на рис. 2.
Таблица 2
Значения перемещений, % по длине элементарной нити при разных нагрузках
|
Длина элементарной нити, на которой фиксировали значение перемещений, от общей длины, % |
Длина элементарной нити, мкм |
||
|
10 |
30 |
100 |
|
|
100 |
0,026 |
0,028 |
0,029 |
|
90 |
0,024 |
0,025 |
0,027 |
|
80 |
0,022 |
0,023 |
0,025 |
|
70 |
0,020 |
0,021 |
0,022 |
|
60 |
0,018 |
0,018 |
0,020 |
|
50 |
0,015 |
0,016 |
0,017 |
|
40 |
0,013 |
0,014 |
0,015 |
|
30 |
0,011 |
0,012 |
0,012 |
|
20 |
0,009 |
0,009 |
0,010 |
|
15 |
0,007 |
0,007 |
0,007 |
|
10 |
0,004 |
0,005 |
0,005 |
|
5 |
0,002 |
0,002 |
0,003 |
|
0 |
0,000 |
0,000 |
0,000 |
В результате проведенных расчетов установлено, что при увеличении длины элементарной нити, значения перемещений по своей абсолютной величине не изменяются, а только перераспределяются по его длине. Величина удлинения, при которой происходит разрыв элементарной нити, составляет 0,78 % (табл. 1), что соответствует результатам экспериментальных исследований. При построении модели элементарной нити с металлическим покрытием размер конечных элементов уменьшили до 25 нм. Для расчетов использовали данные, приведенные в табл. 3.
Таблица 3
Характеристики элементарных нитей с покрытием из нержавеющей стали
|
Показатели |
Толщина покрытия, нм |
||
|
50 |
100 |
200 |
|
|
Модуль Юнга, ГПа |
282 |
299 |
332 |
|
Линейная |
5,7 |
6,5 |
8 |
Результаты расчета перемещений, проведенные для элементарной нити с покрытием из нержавеющей стали и титана при толщине 50, 100 и 200 нм, приведены в табл. 3 и частично показаны на рис. 3.
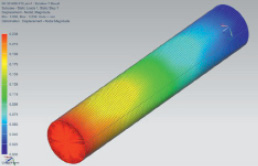
а)

б)
Рис. 3. Результаты расчета перемещений (а) и напряжений (б) элементарной нити с покрытием из нержавеющей стали, при толщине покрытия 50 нм
Погрешность определяли путем сравнения результатов теоретических и экспериментальных исследований (табл. 1 и табл. 4). Если предположить, что толщина покрытия на элементарной нити составляет 100 нм, то в этом случае погрешность для покрытия из нержавеющей стали составит 4,1 и 5 % для покрытия из титана. Аналогичным образом определим значения перемещений для покрытий из цинка, алюминия, серебра и меди.
Таблица 4
Теоретические значения перемещений в зависимости от толщины и типа металлического покрытия на углеродной ленте Луп
|
Тип металлического покрытия |
Толщина металлического покрытия, нм |
Перемещения, % |
|
Без покрытия |
0,78 |
|
|
Нержавеющая сталь |
50 |
0,76 |
|
100 |
0,72 |
|
|
200 |
0,64 |
|
|
Титан |
50 |
0,69 |
|
100 |
0,63 |
|
|
200 |
0,54 |
|
Созданные теоретические модели элементарных нитей позволяют расчетным путем оценивать значения перемещений в зависимости от толщины нанесенного покрытия. Чем больше толщина, тем ниже деформационные характеристики элементарных нитей, больше модуль упругости и выше величина линейной плотности.
Выводы
В результате проведенных исследований экспериментально определены свойства элементарных нитей, из которых изготовлены углеродные ленты ЛУП и Fibra до после несения на них различных металлических покрытий. Установлено, что после нанесение покрытий имеет место изменение механических свойств элементарных нитей. При нанесении на углеродную ленту ЛУП в качестве покрытия титана, цинка, алюминия и серебра имеет место снижение прочности элементарных нитей на от 13,7 до 28,9 % , а при нанесении покрытия из нержавеющей стали и меди имеет место повышение прочности элементарных нитей на 6 %. Существенно более высокое изменение прочности элементарных нитей при нанесении металлических покрытий имеет место при использовании углеродной ленты Fibra, для которой металлические покрытия из нержавеющей стали, титана, меди и серебра приводят к повышению прочности элементарных нитей на 54 %, 44 %, 47 % и 26 % соответственно.
Создана модель элементарной нити с покрытием, которая позволила провести оценку напряженно-деформированного состояния в зависимости от толщины нанесенного покрытия. Установлено, что покрытия оказывают незначительное влияния на напряженно-деформированное состояние элементарной нити, приводят к его изменению (менее 2 %) при толщине 50 нм и не более 5 % при толщине 200 нм. Созданные модели позволяют проводить выбор типа и толщины металлического покрытия.
Разработка углепластиков с комплексом новых функциональных свойств позволит существенно повысить конкурентноспособность изделий. Такие материалы обеспечат повышение долговечности, снижение себестоимости и повышение эффективности использования углепластиков.
Результаты настоящей работы получены в рамках проекта по теме «Научные исследования по разработке композиционных материалов со структурой управляемого хаоса и их применение в высокотехнологичном производстве» по заданию № 11.7291.2017/БЧ.
Библиографическая ссылка
Нелюб В.А. ОЦЕНКА МЕХАНИЧЕСКИХ ХАРАКТЕРИСТИК УГЛЕРОДНЫХ ЛЕНТ ПОСЛЕ НАНЕСЕНИЯ НА ИХ ПОВЕРХНОСТЬ МЕТАЛЛИЧЕСКИХ ПОКРЫТИЙ // Современные наукоемкие технологии. 2018. № 12-2. С. 330-336;URL: https://top-technologies.ru/ru/article/view?id=37342 (дата обращения: 07.02.2026).



