Информационные технологии с каждым днем все больше и больше пронизывают все стороны нашей жизни, вследствие чего мы вынуждены хранить информацию разного уровня конфиденциальности и обмениваться ею. Поэтому остро встает вопрос обеспечения безопасности передаваемых и хранимых данных. Именно с этой целью в данных системах широко используются различные виды шифрования информации. Существует огромное множество алгоритмов, которыми осуществляется шифрование информации с целью недопущения ее попадания в руки тех, кто не имеет права на доступ к ней. Среди этих шифров выделяется большой слой алгоритмов, основанных на сетях Фейстеля. Весьма широко распространенной моделью построения блочных шифров является сеть Фейстеля. Шифры состоят из ячеек, называемых ячейками Фейстеля. Входными данными каждой ячейки являются ключ и исходные данные. Выходные данные каждой ячейки – это измененный ключ и измененные данные. По причине однотипности всех ячеек принято считать сеть многократно повторяющейся структурой. Один из таких шифров – блочный шифр ТЕА, являющийся одним из наиболее простых в своем семействе.
Цель исследования: разработать модификацию блочного шифра ТЕА, которая будет лишена уязвимости к атакам на «связанных ключах».
Для достижения указанной цели был определен ряд задач:
– проанализировать оригинальный алгоритм и существующие его модификации;
– изучить общие принципы атак на связанных ключах, а также реализации их применительно к алгоритму TEA;
– модифицировать алгоритм, применив известные принципы защиты от атак.
Материалы и методы исследования
Блочный шифр Tiny Encryption Algorithm (TEA), представленный в 1994 г. на конференции по быстрым алгоритмам шифрования в г. Лёвен, Бельгия, разработанный Роджером Нидхэмом и Дэвидом Уилером, является одним из самых простых и малых представителей семейства шифров на основе сети Фейстеля [1]. В его основе – битовые операции с 128-битным ключом шифрования, 64-битными блоками и обеспечивающая несимметричность сети Фейстеля операция сложения по модулю 232.
Достоинства шифра. Алгоритм достаточно легко реализовать на любом языке программирования. При правильном исполнении, за счёт малого размера кода, а также благодаря возможности оптимизации под исполнение на 32-битных процессорах, TEA показывает высокую скорость выполнения. Для эффективной диффузии алгоритму требуется не менее 16 циклов, то есть 32 раундов. Стоит отметить, однако, что для полной диффузии достаточно 12 раундов [2]. Шифр TEA считается устойчивым как к линейному [3], так и к дифференциальному криптоанализу.
Описание алгоритма. Исходная последовательность представляется в виде 64-битных блоков. Ключ шифрования, в исходном виде составляющий 128 бит, разбивается на 4 подключа равных размеров (каждый по 32 бита). На этом подготовительный этап считается завершённым [1]. Далее, как правило, на протяжении 32 циклов (64 раундов), происходит процесс шифрования, схематично показанный на рис. 1, где:
<< и >> – операции побитового сдвига влево и вправо соответственно,
? – операция сложения чисел по модулю 232,
⊕ – побитовое исключающее «ИЛИ» (XOR),
Delta (δ) – константа, выведенная из золотого сечения:
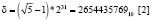 .
.
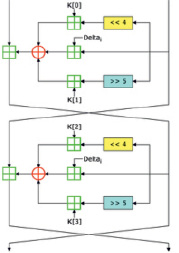
Рис. 1. Схема сети Фейстеля алгоритма TEA
Желая предотвратить атаки, в основе которых лежит симметричность раундов, в каждом из них умножаем константу на номер цикла i.
Атаки на связанных ключах. По причине простого расписания ключей главной уязвимостью алгоритма является возможность проведения «атак на связанных ключах» [4].
Атака на связанных ключах являет собой вид криптографической атаки, в рамках которой номинальный злоумышленник имеет возможность следить за шифрованием или расшифрованием, использующими совокупность закрытых ключей [5]. Эта атака не осуществляется простым перебором значений возможных ключей. В самом начале точные значения ключей неизвестны злоумышленнику, но предполагается, что криптоаналитик знает некое математическое соотношение, которое связывает ключи между собой [6].
Эквивалентные ключи. Наличие эквивалентных ключей так же является слабым местом Tiny Encryption Algorithm. Как известно, каждый ключ имеет три эквивалентных ему подключа. В действительности это означает, что эффективная длина ключа равна 126 бит, а не 128, как было предусмотрено изначально. Из этого следует, что нежелательно использовать ТЕА как хэш-функцию [7]. По причине того, что ТЕА это блочный алгоритм шифрования с 64-бытным блоком, а длина данных не обязательна будет кратна 64 битам, значения всех байтов, которые дополняют блок до кратности 64 битам, устанавливаются в 0х001.
Рассмотрение выбранной уязвимости. Известно несколько атак на TEA, использующих уязвимость связанных ключей. Чтобы понять суть этой уязвимости, рассмотрим самую простую атаку [6].
Пусть имеется ключ K = (K0, K1, K2, K3). Изменим в ключах K2 и K3 биты на позиции 30 (следующие после наиболее значащих бит). С вероятностью приблизительно равной 0,5, выход чётных раундов сети Фейстеля, использующих изменённые ключи, будет совпадать с выходом на оригинальных ключах. Данный факт уже даёт двухраундовую циклическую дифференциальную характеристику с вероятностью 0,5, а соответственно, и 60-раундовую характеристику с вероятностью 2-30. Таким образом, для взлома 64-раундового алгоритма TEA достаточно одной пары «совпавших» ключей и 234 открытых текстов. Возможность такой атаки связана с тем, что алгоритм TEA не предполагает никакой выработки раундовых ключей, а просто использует 4 подключа на протяжении всех раундов.
Результаты исследования и их обсуждение
Очевидное решение описанной выше проблемы – добавить алгоритм выработки раундовых ключей. Ключи не должны создаваться одинаково, линейно. В идеальном случае каждый бит ключа должен влиять на все раунды, причём на каждом раунде по-разному [1].
В целом требования к хорошим алгоритмам выработки раундовых ключей сильно пересекаются с требованиями к криптографическим хэш-функциям.
Достоверно известно, что хорошим расписанием ключей обладает алгоритм DES [6]. Хоть набор раундовых ключей и является результатом несложных линейных преобразований, эти ключи достаточно надёжны и устойчивы к атакам на связанных ключах.
Такое сочетание простоты и надёжности – именно то, чем обладает шифр TEA в целом и чего так не хватает его раундовым ключам. И именно из-за этих качеств было решено модифицировать оригинальный TEA, добавив адаптированный вариант алгоритма выработки раундовых ключей, используемого в DES.
Оригинальный алгоритм расписания ключей шифра DES включает несколько шагов:
1. На вход поступает исходный ключ длиной 56 бит (7 байт). Он дополняется проверочными битами на позициях 8, 16, 24, 32, 40, 48, 56, 64, так, чтобы в каждом байте было нечётное количество единиц.
2. К расширенному ключу (длины 64) применяется начальная перестановка, заданная таблицей из 56 элементов так, что в последовательности, прошедшей перестановку, бит, номер которого соответствует номеру ячейки таблицы, является в исходном (расширенном) ключе битом с номером, указанном в текущей ячейке. Помимо перемешивания битов, в ходе перестановки также происходит и уменьшение длины ключа. Эта перестановка отбрасывает проверочные биты, упомянутые в п. 1. Данная таблица заранее известна и используется шифром независимо от ключа или открытого текста.
3. Далее, в течение 16 циклов, вырабатываются непосредственно раундовые ключи. На каждой итерации ключ представлен в виде двух блоков по 28 бит. Каждый из блоков циклически сдвигается вправо на 1 или 2 бита согласно таблице сдвигов.
4. Затем, объединённые блоки подвергаются второй перестановке, в ходе которой из 56 бит выбираются 48, которые и составляют ключ раунда. Соответственно, в ходе шестнадцати итераций генерируются 16 ключей длины 48.
Из описания оригинального алгоритма видно, что хоть он и достаточно прост, в нашем случае он всё же должен быть модифицирован. Алгоритм TEA предполагает использование раундовых ключей длины 32, а не 48. К тому же 16 ключей – слишком мало: нам необходима возможность создавать от 16 до 128 ключей. Для удовлетворения этих требований оригинальный алгоритм расписания ключей DES был усовершенствован. Но, так как он надёжен именно в исходном виде, было решено не изменять его, а дополнить:
1. Найти способ увеличить длину раундового ключа с 48 до 64. Это позволит за одну итерацию алгоритма выработки раундового ключа, на самом деле создавать два ключа по 32 бита.
2. Увеличивая длину вырабатываемого ключа, только за счёт дополнительных 16 бит внести вариативность ключей, которая позволила бы создавать до 64 пар уникальных раундовых ключей (так как за одну итерацию алгоритма вырабатывается сразу 2 ключа, в сумме получим необходимые нам 128 ключей).
Оригинальный алгоритм расписания ключей описывает 8 проверочных бит, которые никак не участвуют в шифровании. Для расширения размеров и количества итоговых ключей в модифицированном алгоритме решено было использовать именно их.
1. На этапе начальной перестановки, до цикла выработки ключей, создаётся блок расширения. Для этого с помощью подобранной нами таблицы расширения, из 8 проверочных бит получается блок длины 64. Далее, этот блок делится на два равных подблока (левый и правый). Начальные преобразования оригинального алгоритма на данном этапе остаются неизменными.
2. На каждой i-й итерации создания ключей и блоки ключа (как и в исходном алгоритме), и блоки расширения, подвергаются циклическому сдвигу, согласно таблице сдвигов. Однако, чтобы исключить генерацию одинаковых ключей, сама таблица сдвигов была увеличена в 4 раза. Первые 16 сдвигов остались неизменными, а последующие отрезки по 16 сдвигов получаются умножением каждого элемента на (i div 16) + 1, а затем перемешиванием некоторых дополнительных элементов и целых отрезков. Сдвиг блока ключа определяет элемент i таблицы сдвигов, а сдвиг блока расширения – элемент (63 – i).
3. Сдвинутые блоки попарно конкатенируются (левые с правыми).
4. Блоки подвергаются раундовой перестановке точно так же, как в исходном алгоритме.
5. Выбираются границы обрезки блоков. Для блока расширения, начало и конец обрезки задаются следующими формулами:
Hp = i mod 16, Kp = Hp + 32.
Для блока ключа:
Hk = (Hp + 7) mod 16,
Kk = Hk + 32,
где Нр – начало обрезки блока расширения, Кр – конец обрезки блока расширения, Нк – начало обрезки блока ключа, Кк – конец обрезки блока ключа.
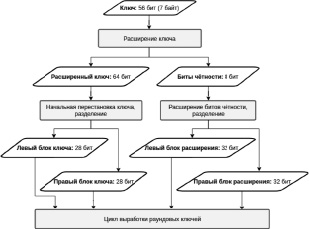
Рис. 2. Начальный этап алгоритма выработки ключей
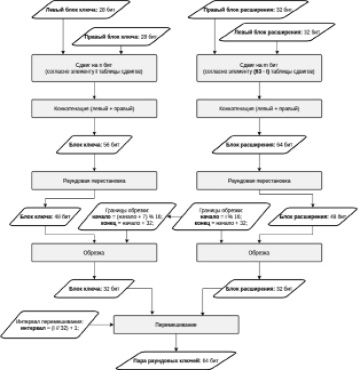
Рис. 3. Цикл генерации раундовых ключей
6. Блоки обрезаются согласно выбранным границам. На данном этапе оба блока имеют длину 32.
7. Выбирается интервал перемешивания: И = (i div 32) + 1.
8. Производится объединение (и перемешивание) блока ключа с блоком расширения согласно выбранному интервалу расширения. Смысл интервала состоит в том, каким образом будут перемешаны элементы обоих блоков. Например, если блок ключа – K = ki, блок расширения – E = ei, то при i = 1, элементы будут перемешаны следующим образом:
{k0, e0, k1, e1,…};
при i = 2:
{k0, k1, e0, e1,…}.
Объединённый и перемешанный блок имеет длину 64. После разделения его пополам получаем пару готовых раундовых ключей.
Оценка результатов. Для измерения надёжности и эффективности разработанного алгоритма были разработаны и использованы несколько простых программных тестов.
Первый тест измеряет время полного шифрования и расшифрования (включая выработку ключей) на данных различных размеров (от 10 Кб до 1 Мб).
Как видно на графике, приведённом на рис. 3, с увеличением объёма данных время работы алгоритма растёт линейно. Как минимум, это говорит о том, что модифицированный алгоритм по временным показателям не уступает оригинальному TEA.
Далее был протестирован отдельно алгоритм выработки ключей. Как видно на рис. 4, выработка 10 000 наборов раундовых ключей из исходного ключа «the_key» в сумме заняла 24062 мс. Другими словами, выработка одного набора в среднем занимает 2,4 мс.
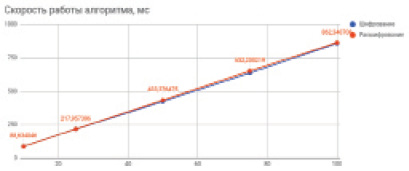
Рис. 4. График изменения скорости шифрования и расшифрования в зависимости от объема данных (от 10 Кб до 100 Кб)

Рис. 5. Вывод теста алгоритма выработки раундовых ключей

Рис. 6. Результаты теста наличия пар эквивалентных ключей
Для проверки защищённости алгоритма от атак, связанных с наличием эквивалентных ключей, был использован отдельный тест. Даже для самых простых и небезопасных ключей шифрования, алгоритм генерирует 128 уникальных, неэквивалентных ключей.
Выводы
Проанализируем этот результат. Уязвимость оригинального TEA связана с тем, что при изменении старших бит некоторых раундовых ключей, результат шифрования не менялся. В нашем же алгоритме изменение любого бита исходного ключа приводит к изменению набора битов чётности, что в свою очередь приводит к существенному изменению всего набора раундовых ключей. Иными словами, в чистом виде старую уязвимость уже можно считать закрытой.
Таким образом, с минимальными временными и ресурсными потерями мы получили более надёжную модификацию алгоритма TEA.
Библиографическая ссылка
Клёкта С.А., Чесноков Н.И., Черкесова Л.В. РАЗРАБОТКА КОМБИНИРОВАННОГО АЛГОРИТМА ШИФРОВАНИЯ НА ПРИМЕРЕ ОБЪЕДИНЕНИЯ БЛОЧНЫХ ШИФРОВ TEA И DES // Современные наукоемкие технологии. 2018. № 12-2. С. 276-281;URL: https://top-technologies.ru/ru/article/view?id=37333 (дата обращения: 27.02.2026).



