При проектировании системы автоматического управления после решения задачи обеспечения устойчивости возникает проблема обеспечения требуемых показателей качества переходных процессов: перерегулирования, времени регулирования и других. Зачастую эти требования являются противоречивыми, что связано в первую очередь с особенностями функционирования систем. Например, при уменьшении перерегулирования происходит увеличение времени регулирования и наоборот; таким образом, две эти величины имеют обратную зависимость. Представить указанную зависимость для сложных систем в математическом виде невозможно, что объясняется особенностями каждого класса систем и входящих в систему подсистем, однако для решения задачи синтеза необходимо определить такие параметры, чтобы система удовлетворяла заданным требованиям.
Целью исследования является решение задачи проектирования САУ ГПА с заданными показателями качества на всех рассматриваемых режимах функционирования.
Для описания системы используются методы теории управления, а именно частотные методы. Одним из инструментов решения поставленной задачи является нейро-нечеткое моделирование на основе которого генерируются системы нечеткого вывода.
Описание модели систем управления газоперекачивающими агрегатами
В настоящее время наряду с применением газотурбинного двигателя (ГТД) в составе силовых установок самолетов и вертолетов их используют и в наземных установках, например на электростанциях в качестве привода генератора. При этом могут использоваться как специально разрабатываемые газотурбинные установки (ГТУ), так и авиационные двигатели, целенаправленно конвертированные для функционирования в системах наземных энергетических установок и ГПА [1].
На рис. 1 представлена модель системы управления газоперекачивающим агрегатом.
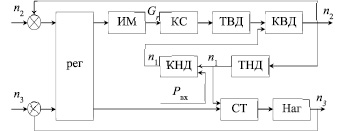
Рис. 1. Структурная схема регулирования ГПА
Введены следующие обозначения:
Pвх – входное давление;
n1, n2, n3, – частоты на соответствующих участках;
ИМ – исполнительный механизм;
КВД – корпус высокого давления;
КНД – корпус низкого давления;
ТВД – турбина высокого давления;
ТНД – турбина низкого давления;
СТ – силовая турбина;
КС – компрессорная станция.
Регулирование топлива осуществляется по частоте вращения СТ. В качестве задания частоты вращения СТ выбирается то значение частоты вращения СТ, которое было в момент достижения частоты вращения малого газа.
Специалисты, на основании информации, касающейся эксплуатации газогенераторных перекачивающих агрегатов в течение последних 10 лет, установили, что выход их строя в большей степени сопряжен со следующими проблемами [2, 3]:
- ошибки при проектировании устройства.
- дефекты, допущенные при производстве агрегата и его сборке, а также монтажа.
- неисправности материалов.
Система управления ГПА должна иметь три уровня, на каждом из которых решается своя задача. Наиболее тесно связанными представляются задачи локального управления ГПА и управления ГПА в составе КЦ. Эти задачи должны решаться децентрализованной системой, на нижнем уровне которой находятся однотипные локальные САУ ГПА, количество которых совпадает с количеством ГПА в компрессорном цехе. С точки зрения математического обеспечения задача локального управления ГПА является достаточно тривиальной, она решается классическими ПИ- и ПИД-регуляторами. Нелинейность и многомерность газотурбинного двигателя как объекта управления приводят к необходимости введения нескольких контуров обратной связи, иногда с переменными (адаптивными) коэффициентами усиления.
В работе [4] предложено описание сложных динамических систем через характеристики подсистем и многомерные элементы связи между ними. В качестве индивидуальной характеристики отдельной подсистемы рассматривается ее передаточная функция в режиме управления, когда подсистема функционирует в изолированном от других подсистем состоянии.
При проектировании систем управления следующей задачей после достижения устойчивого функционирования ставится задача выполнения заданных показателей качества переходных процессов [5]. Зависимость рассматриваемых величин от параметров синтезируемой системы можно представить в виде системы уравнений:
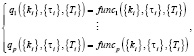 (1)
(1)
где q1,…,qp – показатели качества рассматриваемых переходных процессов;
{ki}, {τi}, {Ti} – множества изменяемых параметров системы (коэффициентов усиления, постоянных времени и т.д.);
func1,…, funcp – функции, выражающие зависимость показателей качества системы от параметров синтезируемых регуляторов.
Рассмотрим в качестве основных показателей качества систем перерегулирование и время регулирования подсистем. Тогда система уравнений (1) примет вид
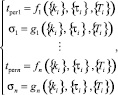 (2)
(2)
где σ1,…,σn – перерегулирование, tрег1,…, tрегn – время регулирования переходных процессов подсистем.
Показатели качества функционирования, предъявляемые к каждой подсистеме, могут отличаться в зависимости от функционального назначения и режима функционирования системы. При построении логического многосвязного регулятора для каждого режима синтез параметров проводится отдельно с целью последующего объединения.
Методы интеллектуального анализа данных при решении задачи синтеза
Построенные математические модели ГПА являются сложными для анализа и синтеза регуляторов, в связи с этим при проектировании используются методы интеллектуального анализа данных: методы распознавания и оценки технического состояния (объекта, ГТД, ГПА), методы интеллектуального управления, методы нелинейного управления, методы теории многосвязных систем автоматического управления, теории систем искусственного интеллекта.
Представить зависимость показателей качества функционирования системы от параметров подсистем и связей между ними в математическом виде очень сложно, что объясняется особенностями каждого класса систем и входящих в сложную систему подсистем. Показатели перерегулирования и времени регулирования имеют обратную зависимость, также сказывается взаимное влияние подсистем друг на друга. Однако существуют различные методы, позволяющие решить поставленную задачу.
В качестве инструментов синтеза параметров систем управления сложными объектами могут использоваться инструменты анализа данных, такие как искусственные нейронные сети, нечеткая логика, машинное обучение, эволюционные вычисления, генетические алгоритмы и т.д. В качестве наиболее подходящего выбран метод синтеза с использованием адаптивных нейро-нечетких сетей.
Адаптивные нейро-нечеткие сети объединяют в себе достоинства систем нечеткого вывода и нейронных сетей. С одной стороны, они позволяют разрабатывать и представлять модели систем в форме правил нечетких продукций, которые обладают наглядностью и простотой содержательной интерпретации, а с другой стороны, для построения правил нечетких продукций используются методы нейронных сетей, что является более удобным и менее трудоемким процессом для проектировщиков.
Например, при построении нейро-нечеткой сети, реализующей принятие решений по выбору параметров системы с целью удовлетворения заданным показателям перерегулирования, используется алгоритм, описанный в работах [6, 7]. Выбор осуществляется по нескольким критериям: коэффициенты усиления и постоянные времени в перекрестных неголономных связях. На рис. 2 представлена структура рассматриваемой системы нечеткого вывода.
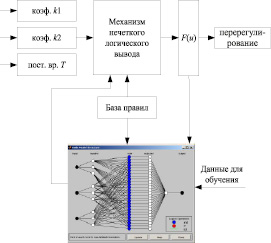
Рис. 2. Структура системы нечеткого вывода
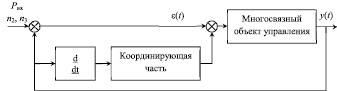
Рис. 3. Координирующая часть нейро-нечеткого регулятора в структурной схеме САУ
Качество обучения разрабатываемой сети напрямую зависит от количества примеров – объема обучающей выборки, и насколько полно примеры описывают данную задачу. Вся информация, используемая нейро-нечеткой сетью для построения системы нечеткого вывода, содержится во множестве обучающих выборок. При этом функции принадлежности синтезированных систем настроены (обучены) так, чтобы минимизировать отклонения между результатами нечеткого моделирования и экспериментальными данными [8].
Аналогично проводится нейро-нечеткое моделирование при увеличении количества и сложности требуемых параметров. Для построения нейро-нечеткой сети в работе используется приложение программного комплекса MatLab – редактор ANFIS, с помощью которого автоматически синтезируется нейро-нечеткая сеть. Последовательность процесса разработки модели нейро-нечеткой сети имеет вид:
1) подготовка обучающей выборки;
2) загрузка обучающих данных;
3) построение структуры системы нечеткого вывода;
4) визуализация структуры гибридной сети.
Результаты обучения нейро-нечеткой сети экспортируем в рабочую область MatLab после чего их можно будет использовать в пакете Simulink, загрузив в блок Fuzzy Logic Controller, который будет выступать в качестве координирующей части нейро-нечеткого регулятора [9]. Расположение координирующей части в структурной схеме многосвязной САУ представлено на рис. 3.
Обученная сеть позволяет подбирать параметры САУ с учетом требуемых показателей качества, что дает возможность корректировать работу системы при изменениях условий функционирования.
Пример проектирования системы управления
Рассмотрим задачу обеспечения заданных показателей качества на одном из режимов функционирования. Для рассматриваемого режима заданы требования к показателям переходных процессов (2) в следующем виде:
{tрег} = {2; 2},
{σрег} = {0,2; 0,2}. (3)
Проведен синтез структуры системы, обеспечивающей устойчивость и заданные показатели устойчивости на заданном конкретном режиме согласно алгоритму [5, 10].
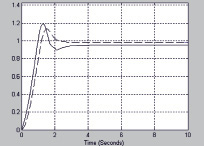
Рис. 4. Графики переходных процессов САУ
При моделировании получены графики переходных процессов, представленные
на рис. 4.
Как видно из рис. 4, синтезированная система обладает заданными показателями качества (3), то есть перерегулирование и время регулирования удовлетворяют требованиям. Аналогично проведены операции определения требуемых параметров на всех режимах функционирования системы, затем проводится агрегирование результатов. Полученные результаты моделирования подтверждают эффективность разработанного метода синтеза.
Заключение
Таким образом, предложена процедура формирования многомерных связей в многосвязной системе управления, которая обеспечивает требуемые показатели качества. Проанализированы возможности повышения качества переходных процессов системы при различных распределениях связей между объектами с использованием нейро-сетевого моделирования.
Работа выполнена при поддержке гранта РФФИ № 17-48-020956 р_а «Математическая модель и алгоритмы управления газотурбинным двигателем, работающим на природном газе и предназначенным для газоперекачивающих агрегатов».
Библиографическая ссылка
Ильясов Б.Г., Саитова Г.А., Халикова Е.А. СИНТЕЗ АЛГОРИТМОВ ИНТЕЛЛЕКТУАЛЬНОГО УПРАВЛЕНИЯ ГАЗОПЕРЕКАЧИВАЮЩИМ АГРЕГАТОМ С УЧЕТОМ ОБЕСПЕЧЕНИЯ ТРЕБУЕМОГО КАЧЕСТВА // Современные наукоемкие технологии. 2018. № 12-2. С. 271-275;URL: https://top-technologies.ru/ru/article/view?id=37332 (дата обращения: 07.02.2026).



