При проведении АТЭ ДТП следственные органы перед экспертами чаще всего ставят следующие вопросы [1]:
1. С какими скоростями двигались ТС в моменты возникновения опасной ситуации на дороге и столкновения (наезда)?
2. Имели ли водители техническую возможность предотвратить ДТП путем экстренного торможения или маневра?
3. Соответствовали (или не соответствовали) действия участников ДТП требованиям правил дорожного движения, и какие несоответствия послужили причиной ДТП?
Как известно [2], для ответа на указанные вопросы при АТЭ эксперты в основном определяют остановочный (So) и тормозной путь (SТ) по следующим формулам:
;
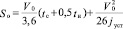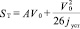, (1)
где V0 – начальная скорость автомобиля, км/ч;
tc, tн – время запаздывания тормозной системы и время нарастания замедления соответственно;
tуст – установившееся замедление;
A – коэффициент, характеризующий время срабатывания тормозной системы [3].
В формулах (1) начальная скорость неизвестна. В случае экстренного торможения из выражений (1) получают [4]:
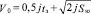; (2)
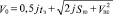, (3)
где j – замедление ТС за время нарастания тормозных сил до максимального значения (tЗ);
Sю – длина пути юза;
Vпс – скорость ТС в момент первого столкновения (наезда).
Анализ рынка сбыта в России за последние три года показывает, что абсолютное большинство легковых автомобилей, продаваемых на территории России, оборудованы АБС [5]. Поскольку ТС с АБС при экстренном торможении практически не оставляют следы юза, то формулы (2) и (3) не могут быть использованы для ответа на поставленные вопросы. Поэтому нужно совершенствовать или разработать новые методы проведения АТЭ, используя законы механики, теорию эксплуатационных свойств АТС, механики сплошной среды и теории пластичности.
Целью настоящей работы является обобщение математических моделей для экспертизы ДТП, позволяющих ответить на главные вопросы, возникающие при АТЭ.
Материалы и методы исследования
Изменение кинетической энергии (работа) ТС при ДТП по времени равно мощности результирующей силы (F) [6]. Например, при наезде на недеформируемое препятствие
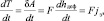
где hдеф – глубина деформации ТС;
tз – интенсивность замедления ТС за период удара.
Все силы, действующие на ТС при ДТП, можно разделить на внешние и внутренние. Пренебрегая работой сил инерции контактирующих деталей ТС, допускаем, что работа внешних сил равна работе сил взаимодействия. К внутренним силам относятся потенциальные и диссипативные. Следовательно, при столкновениях ТС
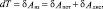
где
;
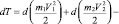
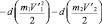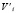– скорость ТС после столкновения (наезда).
Приращение работы потенциальных сил равно сумме приращения работы упругой и пластической деформации:
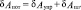
К работе диссипативных сил можно отнести работу трения скольжения, тогда
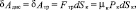(4)
где Fтр, μК – сила и коэффициент контактного трения;
dSК – путь скольжения каждого элемента в зоне взаимодействия ТС;
PК – нормальное давление.
Все ДТП по механике деформации условно можно разделить на три типа: абсолютно упругие, абсолютно неупругие (идеально пластическое тело) и упруго-пластические. Это означает, что в первом случае пренебрегаем пластической (остаточной) деформацией ТС при ДТП. Во втором случае вся кинетическая энергия автомобиля при ДТП затрачивается на пластическую деформацию. Наиболее достоверен третий вариант, когда при ДТП работа деформации включает и пластическую, и упругую составляющие. Для аналитического описания лучше использовать законы сохранения импульса и энергии.
Неупругое столкновение (упругопластическое деформирование объектов взаимодействия при ДТП), в результате которого внутренняя энергия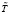 
после столкновения одного или обоих ТС изменяется, и изменяется направление их движения (хотя бы одного).
Запишем импульс каждого ТС после столкновения [2]
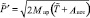. (5)
Для определения возможных направлений движения ТС после столкновения построим векторную диаграмму импульсов (рисунок) в системе отсчета Эйлера.
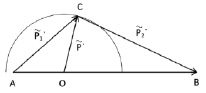
Векторная диаграмма импульсов в случае неупругого столкновения
Импульс ТС с массой m1 P1 = AB делят точкой О на две части, пропорциональные массам ТС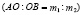 
. Из точки O проводим окружность радиусом P′1, определяемым по формуле (5). Эта окружность является геометрическим местом точек возможных положений вершины треугольника импульсов АВ, стороны АС и СВ которого равны импульсам соответствующих ТС после столкновения.
Покажем вариант оценки предельной скорости или кинетической энергии, при котором кинетическая энергия пойдет только на деформацию, т.е. увеличение внутренней энергии, и после столкновения объекты взаимодействия остаются на месте ДТП или двигаются как одно целое. В системе отсчета Лагранжа это условие можно записать в следующем виде:
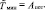
Рассмотрим случай наезда на стоящее ТС, когда кинетическая энергия одного из ТС близка к нулю. Если после столкновения оба ТС не двигались, то их суммарный импульс равен импульсу P1 перед ДТП первого ТС, а кинетическая энергия системы
; 
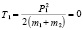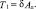
Если после ДТП оба ТС переместились на определенное расстояние вместе, то минимальная кинетическая энергия одного из них, достаточная для их движения, определяется по следующей формуле:
;
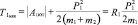или
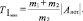(6)
Поскольку
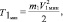(7)
то из формул (6) и (7) находим предельную скорость одного из ТС до столкновения, выше которой они могут двигаться как одно целое, или, наоборот, ниже которой они остаются на месте ДТП. Для этого определим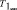 
по следующей формуле:
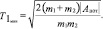(8)
В формуле (8)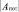 
– это приращение внутренней энергии системы, т.е. энергии, затраченной на работу деформации ТС.
Рассмотрим методы определения работы деформации элементов кузова ТС при ДТП.
Приращение работы деформации конструкции ТС при ДТП можно определить, если известно их напряженно-деформированное состояние [7]:
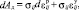
где σij – компоненты тензора напряжения;
, 
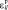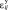– приращение пластической и упругой деформаций каждого отдельного элемента ТС в процессе ДТП.
Связь между напряжениями и деформацией для упругого тела установлена на основе законов Гука и Пуассона:
;
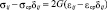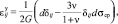(9)
где σср, εср – компоненты шаровых тензоров
(
; 
);
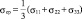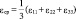δij – символ Кронекера.
В частности, из выражения (9) следует, что
; 
,
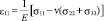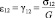где Е – модуль Юнга;
v – коэффициент Пуассона;
G – модуль сдвига (G = E/2(1 + v).
Для малых упругих деформаций [6]
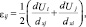
где dUi и dUj – приращение вектора перемещения выделенного элемента (например, прямоугольника на поверхности деформированной детали кузова).
Рассмотрим методы определения приращения работы пластической деформации деталей кузова (кабины) и других конструкций ТС.
Согласно деформационной теории пластичности [7] приращение работы пластической деформации пропорционально приращению (изменению) объема материала и изменения формы изделия:
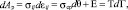
где T – девиатор напряжения (интенсивность касательных напряжений);
Г – интенсивность деформации сдвига.
Если при ДТП не образовались трещины и разрывы, то изменением объема при пластической деформации (в результате увеличения плотности дефектов) dθ можно пренебречь. Тогда
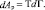(10)
Если известны компоненты тензора деформации εij, то Г определяют по следующей формуле:
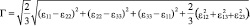(11)
Интегрированием формулы (10) работу пластической деформации не можем определить, так как Т зависит от Г. Следовательно, нужно использовать дополнительные условия или различные теории пластичности. В частности, если девиатор напряжений Т = τs,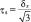 
равен пределу текучести материала (стали, алюминиевых сплавов), то вместо выражения (10) можно использовать формулу Генке [7]:
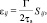(12)
где Sij – компоненты тензора девиатора напряжений, характеризующие изменение формы (конфигурации) рассматриваемого элемента детали,
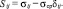
Нужно отметить, что выражение (12) не взаимно однозначно, т.е. если известны значения εij, то можно найти значения Sij, так как по формуле (11) определяется и девиатор деформации. Если заданы Sij, то невозможно найти εij, поскольку неизвестен девиатор деформации Г.
В необратимых процессах деформации ТС при ДТП очень сложно оценить деформированное состояние, еще сложнее определить напряженное состояние, соответственно, и работу деформации. В теории обработки давлением установлено, что девиатор напряжений пропорционален девиатору скоростей деформации.
Компоненты тензора скоростей деформации ηij определяются дифференцированием dεij:
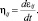
Тогда имеем
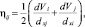
где dVi и dVj – приращение скоростей сдвига за кульминационный период ДТП отдельного геометрического элемента детали ТС.
В этом случае уравнение теории течения для развитой пластической деформации (уравнение Сен-Венана – Мизеса) имеет следующий вид [7]:
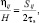(13)
где H – характеризует интенсивность скорости деформации сдвига
; 
.
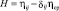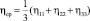Результаты исследования и их обсуждение
Для определения Sij по формулам (12) и (13) эксперту следует последовательно описывать процесс геометрической деформации элементов автомобиля при ДТП до получения конечной картины в этой зоне. Для этого, как правило, применяют различные математические методы, наиболее известным из которых является метод конечных элементов (МКЭ) [8, 9]. Так, при исследовании ДТП поверхность транспортного средства можно представить как сочетание прямоугольников или треугольников. В подвижной системе координат изменение положения каждого узла можно задать как dUxy и dUyx или как dVxy и dVyx. Соответственно:
; 
; 
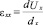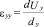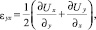
или
; 
; 
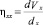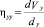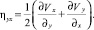
При наличии скользящего удара нужно иметь в виду, что в формуле (4) коэффициент контактного трения скольжения не будет соответствовать коэффициенту трения скольжения в кинематических парах. Допускается изменение его значения в пределах от 0,2–0,5, в зависимости от ряда внешних факторов [7]. Контактное давление (PК) при этом определяется напряженным состоянием в зоне деформации и площадью контакта поверхностей.
Выводы
1. Обосновано, что для проведения АТЭ при столкновениях и наездах необходимо применять математическую модель, основанную на законах сохранения энергии и импульса; деформационной теории пластичности и динамики удара для определения тормозного пути с учетом дорожных условий; описывающая аналитические зависимости для оценки напряженно-деформированного состояния на основе методов конечных элементов.
2. Эксперт, которому поручено провести АТЭ, обязан принять во внимание все введенные идеализации и допущения, а также оценить степень значимости всех факторов, влияющих на результаты экспертизы.
Библиографическая ссылка
Бессарабов Е.Н., Бессарабов А.Н., Гасанов Б.Г., Ефимов А.Д., Нефедов В.В. МАТЕМАТИЧЕСКАЯ МОДЕЛЬ УПРУГО-ПЛАСТИЧЕСКИХ ДЕФОРМАЦИЙ ТРАНСПОРТНЫХ СРЕДСТВ ДЛЯ ПРОВЕДЕНИЯ АВТОТЕХНИЧЕСКОЙ ЭКСПЕРТИЗЫ ДТП // Современные наукоемкие технологии. – 2018. – № 12-2. – С. 262-265;URL: https://top-technologies.ru/ru/article/view?id=37330 (дата обращения: 26.12.2024).