Анализ качества металлургических предприятий, их технических и механических систем позволяет использовать риск-анализ при разработке требований и оценке количественных характеристик рисков, при определении параметров их безопасности и надежности [1–3]. Подавляющее большинство таких металлургических объектов относятся к потенциально опасным. Медленная замена устаревшей, изношенной техники, эксплуатация за пределами грантийных сроков является серьезной проблемой оценки и обеспечения ее безаварийной работы. Процесс эксплуатации потенциально опасных металлургических объектов характеризуется целой совокупностью факторов. Здесь присутствуют: перемещение больших грузов, жидкий расплавленный металл, высокие температуры, широкий спектр частот колебаний – вибраций. Серьезной причиной изменения параметров опасных факторов являются старение, износ, выработка ресурса, что снижает безопасность и повышает риски.
Поэтому, оценка качества потенциально опасных металлургических объектов, эксплуатирующихся за пределами гарантийных сроков, с позиций рисков аварий или, наоборот, их безаварийной работы представляет собой актуальную и важную проблему.
Все исходные опасные факторы, влияющие на оборудование, случайны, выходные обобщенные характеристики безопасности и риска целесообразно представлять в виде вероятностных величин. Таким образом, целью данной статьи является количественная оценка качества, его показателей рассматриваемых объектов, эксплуатируемых за пределами гарантии.
Материалы и методы исследования
Основным показателем качества из множества рассматриваемых будем считать вероятность безопасной эксплуатации за определенное время или весь срок эксплуатации Pб(t), Pб(Tэ) [4, 5].
Производными от этого показателя могут быть среднее время эксплуатации до первой аварии T0, число аварий за время t эксплуатации однотипного оборудования металлургических предприятий. В качестве такого оборудования будем рассматривать несущие конструкции металлургических мостовых кранов, работающих в тяжелых и сверхтяжелых режимах работы.
Вероятность отражает характеристику генеральной совокупности объектов, так как вероятность – это мера множества. С учетом неограниченного пополнения элементов металлургических предприятий можно рассматривать генеральные совокупности как бесконечные.
Будем рассматривать вероятность безопасной эксплуатации на интервале падения (уменьшения) на интервале (Tг, Tэ); Tг – условный срок окончания гарантийного обслуживания однотипного оборудования; Tэ – весь срок эксплуатации.
Рассмотрим период падения вероятности на интервале после окончания срока гарантийного обслуживания. На этом интервале поток событий можно принять пуассоновским, так как возникновение двух и более аварий на бесконечно малом отрезке времени мала (свойство ординарности), а также практически отсутствует последействие (вероятность возникновения аварии на данном отрезке времени почти не зависит от числа и моментов появления аварий на других отрезках – отсутствие последействия), используем известный подход [1]:
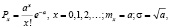(1)
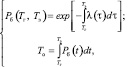(2)
где Tо – среднее время эксплуатации до первой аварии; λ(t) – переменная условная плотность вероятности аварии, при условии, что до этого момента авария не наступила. Иногда этот показатель называют интесивностью потока событий.
Для проектных расчетов, то есть для прогноза, необходимо задать эту функцию на рассматриваемом интервале. Для этого по накопленному опыту эксплуатации подобного оборудования металлургических предприятий необходимо задать сам интервал и характер изменения этой плотности. Учитывая, что аварии – события редкие, соответственно интервалы должны быть значительными (порядка одного года).
Для того чтобы перейти к статистическому оцениванию, на каждом интервале можно считать λ(Ti) = λi = const. Необходимо решить две задачи.
Первая задача – состав генеральной совокупности. Полагаем, что такая совокупность бесконечная, так как количество оборудования на каждом металлургическом предприятии составляет порядка 1200 единиц (на примере Магнитогорского металлургического комбината) [3]. Необходимо отметить, что оборудование выпущено серийно, в разные годы и может отличаться друг от друга, представлено в одном или нескольких экземплярах. Все это накладывает различные ограничения на использование оценок при бесконечной генеральной совокупности.
Вторая задача – определение статистического плана испытаний.
Таким образом, λ(t) – параметр экспоненциального закона распределения. Для него известны оценки максимального правдоподобия и законы распределения этих оценок, позволяющие найти доверительные интервалы [1].
Запишем простое выражение для расчета оценки
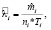(3)
где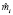 
– количество аварий за определенное время; n – количество единиц техники; Ti – интервал.
Это случайное число имеет закон распределения Пуассона, поэтому верхний односторонний доверительный предел может быть выражен через распределение χ2:
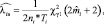(4)
так как квантили распределения Пуассона и квантили «хи-квадрат» связаны соотношением
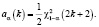(5)
Для случая отсутствия аварий двусторонний доверительный предел будет иметь вид
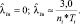
Индекс «н» – нижний предел, индекс «в» – верхний предел.
Для экспоненциального закона, зная верхний доверительный интервал параметра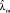 
, можно найти нижний доверительный предел 
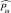вероятности непоявления аварии на интервале Ti, с той же доверительной вероятностью:
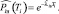(6)
Заметим, что в силу нелинейности функции вероятности оценка максимального правдоподобия будет смещенной, однако на практике обеспечивается p ≥ 0,9 и предыдущее выражение линеаризуется
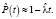(7)
Оценка вероятности безаварийной эксплуатации будет асимптотически почти несмещенной эффективной состоятельной.
Таким образом, получим для интервалов ряд оценок и доверительных пределов:
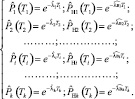(8)
Полагая независимость аварий на различных интервалах времени, можно записать выражение для оценки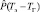 
вероятности безаварийной работы всего оборудования:
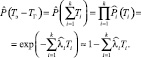(9)
Результаты исследования и их обсуждение
Приведем модельный пример. Исследуем металлургические мостовые краны, работающие в тяжелых и сверхтяжелых режимах, гарантийный срок эксплуатации которых составляет 15 лет [3, 5].
Между небольшими подъемами после технического обслуживания вероятности безаварийной работы следует неуклонное падение и рост рисков аварий.
R(t) = [1 – Pб(t)]M(y). (10)
R – риск оборудования; M(y) – математическое ожидание ущерба.
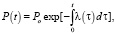(11)
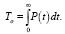(12)
По опыту эксплуатации примем функцию интенсивности аварий линейной [1]:
λ(τ) = 0,005 + 0,003τ. (13)
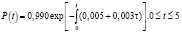(лет).
После интегрирования получим
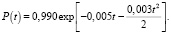
Результаты приведены в таблице и на рис. 1, 2.
Вероятность безаварийной эксплуатации и качества оборудования за пределами гарантийных сроков эксплуатации
|
t |
0 |
1 |
2 |
3 |
4 |
5 |
|
P(t) |
0,992 |
0,986 |
0,976 |
0,964 |
0,949 |
0,932 |
|
R(t) |
0,008 |
0,014 |
0,024 |
0,036 |
0,051 |
0,068 |
|
K(t) |
125,00 |
69,31 |
42,11 |
27,88 |
19,72 |
14,68 |
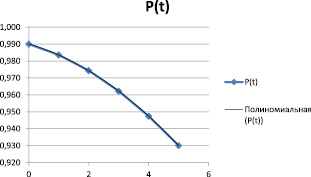
Рис. 1. Вероятность безаварийной эксплуатации за пределами гарантии
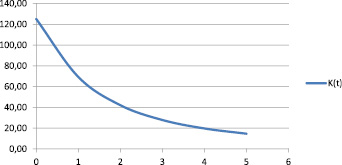
Рис. 2. Качество оборудования за пределами гарантии
Используя методику и расчеты, можем оценить аварийность за пределами гарантийных сроков эксплуатации.
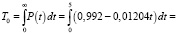
Аппроксимируем P(t) = 0,992 – 0,01204t, t – г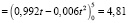оды.
годы.
Это позволяет количественно оценить качество эксплуатируемого оборудования. Так видно, что в относительных единицах качества ниже 20 единиц дальнейшая эксплуатация оборудования после гарантийных сроков эксплуатации нецелесообразна.
Выводы
В настоящее время обеспечение необходимого уровня качества различных сложных технических систем характеризуется системой международных стандартов ИСО 9000. Многогранное понятие качества таких объектов включает множество показателей, основные из которых: надежность, безопасность, долговечность и экономические характеристики. Эти показатели имеют важное значение для построения системы управления качеством металлургических предприятий. На сегодняшний день оценка качества таких технических систем с позиций безопасности и рисков недостаточна. Требования стандарта ИСО 9001:2015 напрямую указывают на расчет, применение и учет рисков, их нормирование.
В соответствии с этим предлагаемая методология позволяет прогнозировать динамику изменения рисков и качества потенциально опасных металлургических объектов – металлургических мостовых кранов, а значит, и управлять технологическими процессами, процессами снижения рисков.
Для таких потенциально опасных металлургических объектов этот подход был применен впервые. Модельный пример показал его достаточную работоспособность.
Предложенный метод расчета статистических и вероятностных характеристик безопасности эксплуатации и рисков оборудования позволяет при приемлемых допущениях решить задачу количественных оценок безопасности его эксплуатации. Примененный подход к потокам событий может быть расширен. Так, можно отдельно оценить риски аварий от отдельных опасных факторов или систем и агрегатов, что будет способствовать более полному описанию потока аварий, а математический аппарат будет таким же.
Такая оценка качества может быть применена и к другим потенциально опасным объектам металлургических предприятий. В конечном итоге она может быть распространена и дополнена и на все металлургическое предприятие в целом.
Библиографическая ссылка
Извеков Ю.А., Гугина Е.М., Анисимов А.Л., Шеметова В.В. ОЦЕНКА РИСКОВ ПОТЕНЦИАЛЬНО ОПАСНЫХ МЕТАЛЛУРГИЧЕСКИХ ОБЪЕКТОВ ЗА ПРЕДЕЛАМИ ГАРАНТИЙНЫХ СРОКОВ ЭКСПЛУАТАЦИИ В МЕНЕДЖМЕНТЕ КАЧЕСТВА ПРОМЫШЛЕННОГО ПРЕДПРИЯТИЯ // Современные наукоемкие технологии. – 2018. – № 11-2. – С. 179-182;URL: https://top-technologies.ru/ru/article/view?id=37299 (дата обращения: 19.04.2024).