Управление в современных машиностроительных и технологических агрегатах, а также приборостроительных и специальных системах сопряжено с необходимостью компьютерной переработки информации в реальном времени [1]. Причиной является необходимость создания цифровых встраиваемых блоков, которые функционируют в совокупности с техническими устройствами системы, получая и выдавая реальные физические сигналы. По существу, эти блоки служат неотъемлемыми частями системы и могут рассматриваться как особые её конструктивные элементы.
Современным инструментом и базой моделирования сложных динамических систем служат не только известные языки программирования «высокого» уровня, но и сравнительно недавно разработанные «символьные математические» языки, или, как их часто называют, системы компьютерной алгебры (математики) [2]. Их можно считать основой, так называемых аналитико-числовых компьютерных технологий (АЧКТ). Универсальные языки высокого уровня послужили базой для автоматизации компьютерной арифметики. Системы АЧКТ являются инструментом для автоматизации символьных (формульных) математических преобразований. Подобные работы традиционно считались предметом только научных исследований, однако практика показывает, что в настоящее время без использования таких средств не могут производиться качественные и глубокие инженерные работы. Это со всей очевидностью проясняется на примерах задач управления, а конкретнее в задачах создания цифровых моделей для встраиваемых в системы управления динамических блоков [3, 4].
Требования повышенного вычислительного быстродействия практически исключили возможность применения известных и популярных методов численного интегрирования дифференциальных уравнений (одношаговых и многошаговых) из-за малого шага дискретности по времени, что приводит к необходимости использования нетрадиционных форм дифференциальных уравнений интегрируемой системы [5].
Предложено вместо традиционной нормальной формы дифференциальных уравнений динамического объекта представлять его соединением вычислительно реализуемых звеньев, названных базовыми звеньями или базовыми блоками [6]. Вычислительно реализуемым звеном назовём блок с передаточной функцией с совпадающими порядками числителя и знаменателя. Естественно, что в их число входят и физически реализуемые блоки, где порядки знаменателя меньше, чем порядки числителя. Соединение блоков может быть последовательным, параллельным или смешанным. Подобное построение системы позволяет проводить её моделирование последовательно во времени, то есть поблочно.
Методы формирования цифровых моделей, адекватных эталонным непрерывным аналогам
Широкое распространение в настоящее время получило использование известной формулы свёртки для реализации цифрового аналога путём «взвешивания» прошлых значений внешних воздействий и откликов на них. Подход апробирован и вполне применим при реализации сравнительно простых динамических преобразований (цифровые фильтры нижних или верхних частот невысокого порядка). Однако здесь имеют место весьма существенные методические и вычислительные ошибки.
Ранее был предложен альтернативный подход многомерного моделирования, (М-моделирование) [6, 7], в котором используется формула Коши, позволяющая на каждой итерации (реализации внешнего воздействия) определить новое начальное состояние. Таким образом, результат моделирования становится инвариантен временному шагу итерации. Здесь вводятся понятия М-характеристик: М-характеристиками будем называть матрицу, вектор-столбец и вектор-строку дискретной многомерной модели динамической системы [6]. Эти объекты и обеспечивают формирование рекуррентного процесса моделирования.
Однако формула Коши применима только для линейных (стационарных и нестационарных) систем, причём в нестационарном случае М-характеристики не выражаются в элементарных функциях, что существенно усложняет задачу [8]. Поэтому метод М-моделирования был развит применительно к стационарным линейным системам. Были разработаны способы и алгоритмы преобразования скалярных и векторных уравнений в систему уравнений состояния, используя форму Фробениуса для матрицы состояния и предложенную автором альтернативную форму на базе широко известного в теории управления понятия типовых звеньев.
Если в первом случае переменными состояния является фазовый вектор выходной переменной, то во втором – собственные движения типовых инерционных звеньев. Первый вариант даёт наглядное (физичное) представление о векторе состояния (выходная переменная и её производные), второй – сопряжён с менее наглядной формой переменных состояния, но ведёт к более простой структуре матрицы системы уравнений (квазидиагональной), что значительно упрощает построение фундаментальной матрицы, а затем и определение всех М-характеристик дискретной цифровой модели.
Недостаток изложенного метода М-моделирования заключается в трудностях его применения к нелинейным и нестационарным системам [9]. Эти сложности и подтолкнули к следующей модификации М-метода: метод многомерного параметрического моделирования (МП-моделирования) [6, 10].
Метод многомерного параметрического моделирования
Основной задачей является стремление сделать М-характеристики параметрическими, чтобы учесть зависимость их от времени (нестационарность) и от состояния (нелинейность). Причём так, чтобы время и состояние входили в соответствующие матрицы явно и позволяли путём подстановки нужного числового значения параметра, меняющегося на каждом шаге, своевременно подстроить матрицы дискретной модели путём замены переменных. Известные математические и ресурсные ограничения не позволяют распространить подход на системы произвольного порядка, однако свойства динамических систем, допускающие структурную декомпозицию «большой» системы на более «мелкие», менее связные, обеспечивают разрешимость задачи.
В настоящей работе предложено предварительно формировать характеристики цифровой М-модели в виде параметрических (аналитических) выражений, которые, используя структурные разложения сложного аналога, могут быть помещены в память ЭВМ в виде параметрических откликов. Рассмотренный подход назван многомерным параметрическим моделированием (МП-моделированием).
Практически важным для реализации МП-моделирования является выбор минимальных и достаточных структурных единиц, для которых будут создаваться параметрические отклики (параметрические М-характеристики) [6]. По нашему мнению, целесообразно использовать метод типовых звеньев для структурирования динамических систем при дискретном моделировании. Но среди типовых звеньев существуют физически нереализуемые, которые, однако, должны войти в число базовых структур. Для этого в состав базовых структур следует включить все инерционные звенья (интегрирующее, апериодическое, двукратное апериодическое – с двукратным действительным полюсом, колебательное), а также объединённое их сочетание с физически нереализуемыми звеньями. Таким образом, в список базовых структур войдут блоки дробно-рациональных передаточных функций не выше второго порядка включительно, которые мы называем вычислительно реализуемыми, т.е. допускается равенство порядков числителя и знаменателя передаточной функции.
Для каждого базового блока были сформированы МП-характеристики. Каждый блок имеет свои входной и выходной сигналы, с помощью которых они объединяются между собой. Причём объединение этих структурных единиц в передаточную функцию системы высокого порядка может производиться последовательно, параллельно или с помощью местных обратных связей.
Далее вычисления могут проводиться как с использованием матриц высокого порядка, соответствующих максимальному порядку моделируемой системы, так и поэтапно с матрицами меньшей размерности [6].
Для каждой типовой структурной единицы необходимо заранее заготовить её дискретные характеристики (М-характеристики) в параметрическом виде, т.е. функции ограниченного числа переменных. Практика показывает, что характер вхождения параметров звеньев в МП-характеристики весьма сложен, однако он всегда может быть выражен в элементарных функциях. Небольшое количество параметров типовых и присоединённых звеньев делают указанную задачу выполнимой, а итоговые формулы сравнительно несложными и обозримыми.
В результате для аналоговых прототипов (слева) получаются рекуррентные процессы (справа):
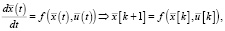
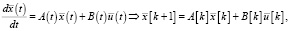
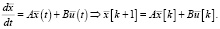
В качестве примера возьмем параметрические выражения для матриц дискретной модели колебательного звена. Для упрощения формул понадобилось ввести другие параметры r и w0 для действительной и мнимой частей полюса вместо общепринятых [].
Матрицы параметрической цифровой модели:
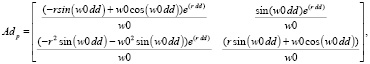
где Ad_p – переходная матрица, Bd_p – матрица входа, dd – длина шага дискретности по времени.
Реализация метода МП-моделирования
На данный момент для разработки и моделирования технических систем обычно используются специализированные программные среды (Matlab, Vissim) либо математические пакеты общего назначения (MathCad, Maple и другие), которые имеют ряд недостатков, проявляющихся вместе либо по отдельности. Основными являются следующие:
- использование стандартных методов численного интегрирования (Рунге – Кутты и др.) без возможности включения других;
- программное обеспечение не позволяет модифицировать алгоритмы;
- ограничены возможности (или отсутствие возможностей) подключения внешних устройств для моделирования сигналов в реальном масштабе времени.
Для апробации и определения эффективности моделирования и оценки полученных результатов потребовалось создание специализированного программного обеспечения (ПО), которое было реализовано на языке программирования высокого уровня Python 3 с помощью свободных программных библиотек PySide (интерфейс пользователя) и Matplotlib (визуализация результатов моделирования).
Данное ПО обеспечивает реализацию следующих функций:
1) привычный для большинства пользователей графический интерфейс (например, Matlab Simulink), ставший стандартом в области моделирования систем;
2) использование типовых графических примитивов из библиотеки вычислительно реализуемых звеньев для объединения в цельную систему;
3) возможность задавания конкретных параметров как для отдельного звена, так и для всей модели;
4) возможность моделирования отклика системы на реальный сигнал, поступающий напрямую со звукового входа персонального компьютера (ПК), либо отклика на программно генерируемые сигналы (гармонические воздействия разной формы, функция Хевисайда);
5) графическое отображение текущего состояния системы в нескольких точках, заданных пользователем;
6) кроссплатформенность программного обеспечения (от Windows 7, до ОС Linux).
Пример использования ПО представлен на рис. 1. Исходными данными является передаточная функция, которая раскладывается на ряд последовательно соединенных стандартных вычислительно реализуемых звеньев из библиотеки, представленной в системе. Далее происходит ввод полученной последовательности звеньев в графическом виде и задание их параметров. Ко входу системы программно подключается звуковая карта, либо виртуальные воздействия, а с контрольных точек снимается цифровой отклик и отображается на графиках.
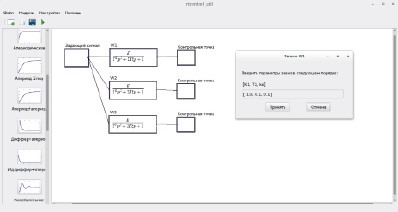
Рис. 1. Задание параметров моделируемой системы средствами разработанного ПО
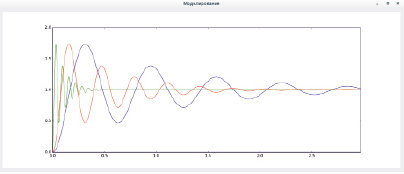
Рис. 2. Результаты моделирования колебательного звена с различными параметрами
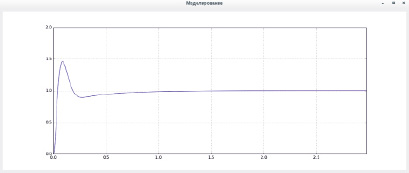
Рис. 3. График переходного процесса в скорректированной нереализуемой замкнутой системе
На рис. 1 показано моделирование трех колебательных звеньев с различными параметрами, подключенных к одному задающему сигналу, а на рис. 2 – результаты моделирования.
В качестве примера реального использования и исследования характеристик созданного ПО рассмотрена задача коррекции свойств неустойчивой системы.
Исходная система состоит из четырех типовых последовательных звеньев – идеального усилительного, идеального интегрирующего, апериодического и колебательного. Ее передаточная функция имеет вид
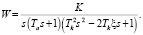
Параметры звеньев системы: K = 1, Ta = 0,01, Tk = 0,2, ξ = –0,6.
После проведения исследования замкнутой системы проведен синтез корректирующего устройства с передаточной функцией
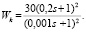
График переходного процесса в скорректированной замкнутой системе показан на рис. 3.
Однако такой вариант системы технически не реализуем, поскольку выходные сигналы блока коррекции будут иметь огромные импульсные составляющие на участках быстрого изменения задающего сигнала из-за наличия дифференцирующих звеньев в корректирующей передаточной функции.
Данная проблема была решена разбиением корректирующей функции на две части:
W1k = 30,
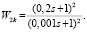
Данная передаточная функция представляет собой набор из трех вычислительно реализуемых звеньев из библиотеки ПО – одного усилительного и двух представляющих собой последовательное соединение дифференцирующего первого порядка и апериодического звеньев. W1k было решено добавить в прямую цепь, а W2k – в цепь обратной связи.
Свойства замкнутой системы улучшатся благодаря изменению обратной связи, однако, поскольку обратная связь остается единичной по постоянной составляющей и дифференцирующей по сути, она не повлияет на статические свойства системы. Но теперь на W2k исключается подача быстро меняющихся воздействий.
Таким образом, была составлена общая передаточная функция замкнутой скорректированной системы (рис. 4).
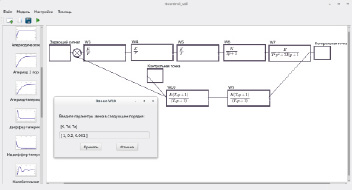
Рис. 4. Структурная схема скорректированной реализуемой системы
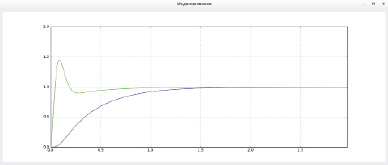
Рис. 5. Переходные процессы в скорректированных реализуемой и нереализуемой замкнутых системах
Переходные процессы в обеих системах показаны на рис. 5.
Как видно из графиков, переходный процесс в реализуемой системе происходит медленнее, но при этом отсутствует перерегулирование.
Моделирование системы производилось с фиксированной величиной шага, равной 0,0001 с, в течение 3 с. Для сравнения данная система также была промоделирована в пакете Matlab. Оба эксперимента проводились с помощью встроенных профилировщиков. Сравнение результатов моделирования с профилированием представлено в табл. 1. Характеристики быстродействия отдельных составляющих модели разработанного ПО представлены в табл. 2.
Таблица 1
Сравнение результатов профилирования длительности расчетов в Matlab и разработанном ПО при моделировании процесса длиной 3 с
|
Метод |
Время, с |
|
Разработанное ПО, метод параметрического моделирования, фиксированный шаг d = 0,0001 с |
0,432 |
|
Matlab, встроенная функция ode45, переменный шаг |
0,83 |
|
Matlab, встроенная функция ode5, фиксированный шаг d = 0,0001 с |
11,83 |
Таблица 2
Характеристики быстродействия отдельных составляющих модели в разработанном ПО
|
Тип звена |
Время расчета одного шага моделирования, мкс |
|
Идеальное усилительное |
0,9 |
|
Идеальное интегрирующее |
1,1 |
|
Апериодическое |
1,2 |
|
Колебательное |
2,1 |
|
Дифференцирующее + апериодическое |
2,2 |
Характеристики быстродействия, приведенные в таблице, показывают, что вычисления методом МП-моделирования являются значительно более быстрыми, чем традиционные методы моделирования технических систем, и не вызывают потери качества и точности моделирования. Время расчета одного шага простого звена лежит в пределах нескольких микросекунд, что позволяет сделать вывод о перспективности использования данного метода в системах реального времени.
В дальнейшем планируется провести работу в части реализации алгоритмов МП-моделирования на более низкоуровневых языках для оптимизации и повышения скорости вычислений. Также представляется возможной генерация низкоуровневых программных модулей для встраиваемых систем, требующих быстрой цифровой обработки сигналов.
Выводы
Разработаны алгоритмы формирования характеристик для базовых динамических структур, поддерживающих рекуррентное моделирование динамических систем широкого класса. Разработано и реализовано ПО для отладки и МП-моделирования систем, позволяющее изменять параметры моделируемых структур, не меняя самих алгоритмов расчета и программы.
Тестовые испытания предложенного программного обеспечения показали, что скорость процесса моделирования возросла по сравнению со стандартными алгоритмами, которые применяются в подобных расчетах, без потери качества и точности моделирования, могут быть эффективно использованы для расчетов и обработки сигналов в системах реального времени.
Библиографическая ссылка
Малахов Н.А., Жигулёвцев Ю.Н. СТРУКТУРНО-ПАРАМЕТРИЧЕСКОЕ МОДЕЛИРОВАНИЕ ДИНАМИЧЕСКИХ ОБЪЕКТОВ И СИСТЕМ УПРАВЛЕНИЯ В РЕАЛЬНОМ ВРЕМЕНИ // Современные наукоемкие технологии. 2018. № 12-1. С. 108-114;URL: https://top-technologies.ru/ru/article/view?id=37271 (дата обращения: 13.02.2026).



