В современном обществе к подготовке будущего учителя математики предъявляются такие требования, как умение адаптироваться к изменяющимся условиям, быстро ориентироваться в меняющемся потоке информации, находить оптимальное решение в каждой конкретной ситуации, использовать новые методики в профессиональной деятельности и взаимодействовать в команде.
К эффективному инструменту, позволяющему осуществлять качественную подготовку будущих учителей, можно отнести проектную деятельность, которая закреплена государством в качестве обязательного компонента учебного процесса [1, 2]. Для бакалавров педагогического образования этот вид деятельности не только соответствует условиям и требованиям реализации ФГОС ВО, но и является существенной составляющей профессиональной деятельности будущего учителя, способствует интеграции в процессе обучения двух видов деятельности: профессиональной и учебной [3, 4]. Именно проектная деятельность дает студентам-бакалаврам опыт поведения в проблемных практических ситуациях, развивает умение решать нестандартные проблемы и соответствовать предъявляемым повышенным требованиям к коммуникационному взаимодействию и сотрудничеству [5–7].
В настоящее время организация проектной деятельности студентов активно обсуждается отечественными [2, 5, 6] и зарубежными [8] исследователями, что в первую очередь обусловлено модернизацией системы высшего образования на основе деятельностного и компетентностного подходов.
Изменение подходов к подготовке будущего учителя математики связано с решением различных проблем, среди которых особенно выделяются такие, как отсутствие тесных межпредметных связей, изолированность профильных дисциплин и недостаточная практическая направленность их содержания. Большой потенциал для установления и развития необходимых для учебной и будущей профессиональной деятельности связей между профильными математическими дисциплинами, для их наполнения практическим содержанием имеет математическое моделирование. К основным функциям математического моделирования в процессе выполнения учебного проекта можно отнести познавательную функцию, управленческую, интерпретационную и прогностическую [9, 10]. Этапы математического моделирования органично встраиваются в этапы выполнения проекта. Введение математического моделирования в качестве компонента в проектную деятельность обеспечит формирование научного мировоззрения, прикладную и профильную направленность математической подготовки бакалавров, системность знаний, развитие их мыслительных операций, необходимых в современных условиях.
Поэтому цель нашего исследования – это выявление и анализ таких методических подходов, условий и требований к тематике и содержанию учебных проектов, а также к организации проектной деятельности по профильным математическим дисциплинам, при которых использование математического моделирования позволяет достигать высоких предметных и метапредметных результатов обучения.
Материалы и методы исследования
Анализ научно-методической литературы, методик и опыта организации проектной деятельности [3, 4, 6], а также применения математического моделирования в учебном процессе [9, 10] позволяет сделать вывод о том, что эффективное решение указанных выше проблем приводит к необходимости использования математического моделирования в учебных проектах по профильным математическим дисциплинам (например, математический анализ, аналитическая геометрия и др.).
Кроме того, важными условиями для эффективной организации проектной деятельности бакалавров в процессе их математической подготовки является наличие площадки для поиска и постановки проектных задач, интеграция проектной деятельности студентов и преподавателей [7, 11], организация презентаций, открытого обсуждения и оценки конечных продуктов проектной деятельности [4].
К требованиям выполнения учебных проектов по профильным математическим дисциплинам мы относим: соответствие уровня знаний студентов, наличие практической составляющей, выход в различные сферы знаний, отсутствие «очевидного решения» и известность решения (в литературе, интернете), мотивация изучения этих дисциплин у студентов, а также признаки новизны в постановке и/или решении задач. Профильные математические дисциплины, в частности математический анализ, дают большие возможности для выбора тем и содержания проектной деятельности [12, 13]. Такие проекты способствуют активизации познавательной деятельности студентов, развивают креативность и когнитивные процессы, навыки групповой коммуникации, являются источником инициативы и творчества.
При изучении математического анализа преподаватель предлагает такие задачи для проекта, решая которые студент не только получит знания по новой теме, но и будет формировать умения использовать их для решения задач из других дисциплин. Особенно продуктивными, по нашему мнению, являются темы, связывающие понятия и методы математического анализа с геометрическими объектами. Выполнение такого проекта позволяет в полной мере вовлекать студентов в реализацию всех этапов математического моделирования.
Предложенные авторами данной статьи методические подходы, условия и требования реализовывались при выполнении учебного междисциплинарного проекта для бакалавров 1 курса физико-математического факультета направления «Педагогическое образование» по профильным дисциплинам «Математический анализ» (раздел – дифференциальное исчисление функции одной переменной) и «Геометрия» (раздел – аналитическая геометрия, кривые второго порядка). Выполняемый проект был направлен не только на формирование конкретного набора знаний, умений и способов действия по конкретным дисциплинам, но и на создание условий для саморазвития и самореализации личности, способной к инновационной профессиональной деятельности. Такой проект может рассматриваться как один из альтернативных вариантов традиционных в вузах типовых расчетов.
Для выполнения учебных проектов преподавателями был составлен набор задач практического содержания без числовых данных и формул в условии. Эти задачи были предложены на выбор студентам на занятии. Студенты распределились на мини-группы по два-три человека. На выполнение и защиту проекта студентам отводился один семестр.
Результаты исследования и их обсуждение
Рассмотрим одну из предложенных студентам задач для выполнения проекта. Представим деятельность студентов и результаты каждого этапа выполнения проекта.
Задача. Требуется изготовить упаковочную коробку для флакона туалетной воды, наибольшее по площади поперечное сечение которого имеет форму эллипса. Какой можно сделать форму поперечного сечения коробки (отличной от эллипса) с целью уменьшения площади сечения? На сколько меньше окажется площадь поперечного сечения по сравнению с традиционной, часто встречаемой прямоугольной формой?
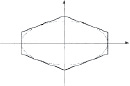
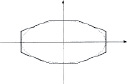
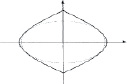
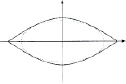
1. На начальном, поисковом этапе проектной деятельности бакалавры находили имеющуюся информацию по проблеме, подбирали примеры реальных форм упаковок, анализировали их, выбирали наиболее подходящие. Преподаватель обращал внимание студентов на существование нескольких возможных решений проблемы. Студенты выявили и исследовали несколько вариантов формы поперечного сечения и сделали выводы о том, какая площадь является наименьшей в каждом из случаев и наименьшей среди выбранных форм. Появлялась необходимость описания форм упаковок с помощью известных студентам фактов о прямых и кривых второго порядка (как наиболее часто встречающихся линиях в реальных ситуациях). На поисковом этапе проектной деятельности осуществляется первый из этапов математического моделирования. Он заключается в анализе возможностей использования математики для решения имеющейся проблемы, в подборе подходящей математической модели. Для поставленной задачи, в результате анализа собранной информации, бакалаврами было предложено несколько вариантов формы поперечного сечения (формы дна) упаковки (таблица).
Варианты форм поперечного сечения упаковки
|
Только прямолинейные границы фигуры |
Только криволинейные границы фигуры |
Комбинированные границы фигуры |
|
|
|
|
2. Второй этап – аналитический, на нем бакалавры выбирали подходящие факты, понятия, практические умения, осуществляли выбор способа решения проблемы и определяли роли участников проекта. Результатом этих действий являлись: формулирование темы проекта, его цель и задачи, определение вида предполагаемого продукта своей деятельности и возможная форма представления продукта. Студентами была предложена следующая тема проекта: «Определение оптимальных размеров некоторых видов упаковок». Математическое моделирование на втором этапе выполнения проекта заключается в тщательном изучении проблемы, отборе параметров, отражающих ключевые свойства моделируемого объекта. На этом этапе студенты формулировали конкретные математические задачи и определяли методы их решения. Таким образом, завершается создание окончательной математической модели и определяются математические методы для ее решения.
Здесь студенты использовали как знания (понятия, теоремы, методы, уравнения линий и их взаимное расположение) из аналитической геометрии, так и знания из математического анализа (понятия, теоремы, методы). Сопоставление понятий из этих двух дисциплин приводит к окончательному виду математической модели, удовлетворяющей условиям задачи и к выбору подходящего метода решения.
В случае поставленной задачи – это поиск формы дна коробки с минимальной площадью: практическая задача на экстремум. Для каждого из случаев, представленных в таблице, студентами была выведена целевая функция и исследована на экстремум.
Для указанных в таблице вариантов форм поперечного сечения упаковки студентами были получены и исследованы следующие виды целевых функций, в которых a, b – полуоси вписанного эллипса, переменная k определяет точку касания эллипса с ограничивающими его линиями:
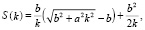
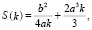
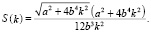
3. На третьем, практическом этапе бакалавры осуществляли обобщение имеющихся знаний, получали полное решение задач, обсуждали уже полученные ими результаты и соотносили их с задачами проекта. На этом же этапе на основе решения полученных задач были сделаны выводы по поставленной проблеме. Этап математического моделирования – это решение полученной математической задачи (вручную, если это не слишком сложно, или с помощью компьютерных средств) и анализ полученных результатов. Студенты интерпретировали полученный математический ответ, то есть перевели его на язык исходной практической задачи.
Заметим, что при решении модели для рассматриваемой задачи студенты использовали различные компьютерные программы, онлайн-сервисы и приложения, как для получения решения, так и для визуализации модели. К таким приложениям в первую очередь относятся свободно распространяемые программные продукты (например, GeoGebra) и бесплатные онлайн-сервисы, например Desmos (www.desmos.com), GeoGebra Graphing Calculator (www.geogebra.org/graphing).
4. На четвертом, презентационном этапе бакалавры определились с форматом представления проекта и провели публичную защиту проекта – доклад с презентацией и демонстрацией проектного продукта, который был представлен как в виде макета упаковки, так и в виде чертежа для изготовления упаковки с указанными размерами и формулами. Во время презентации студенты не только рассказали о ходе работы и представили результаты, но и продемонстрировали собственные знания и опыт в решении проблемы проекта, приобретенные компетенции. Регламент защиты проекта и представления продукта, как правило, составляет 10–15 мин на выступление.
На этом этапе формируются навыки использования научного стиля в письменной и устной речи, развивается умение выбирать самое главное, коротко и ясно излагать свои мысли, отрабатывается техника публичных выступлений. Кроме того, студенты получают возможность максимально раскрыть свой творческий потенциал.
5. Пятый, заключительный этап проектной деятельности, – рефлексивно-оценочный. На этом этапе студенты обсудили проведение презентации, заданные вопросы и свои ответы на них, провели рефлексию своей деятельности и оценку собственных достижений.
На этом этапе студенты дали положительную оценку новому для них виду деятельности, продемонстрировали свою заинтересованность и высокую мотивацию изучения достаточно сложных профильных математических дисциплин, высказали свое желание продолжить выполнение учебных проектов по другим математическим дисциплинами.
Четвертый и пятый этапы выполнения проекта, собственно, не содержат математического моделирования. Поэтому можно сделать вывод, что математическое моделирование не может заменить проектную деятельность в учебном процессе при формировании определенных требованиями ФГОС ВО профессиональных компетенций бакалавров педагогического образования.
Заключение
Таким образом, организация проектной деятельности бакалавров с использованием математического моделирования способствует реализации прикладного и интеллектуального потенциала профильных математических дисциплин в учебном процессе, позволяет создавать образовательную среду, в которой студенты мотивированы на самостоятельный поиск и приобретение исследовательских умений (постановка проблемы, сбор и анализ информации, выдвижение гипотез, обобщение, прогнозирование). Выполнение проектов студентами также повышает мотивацию студентов к изучению профильных математических дисциплин, позволяет осознанно и динамично воспринимать новые знания, глубже и эффективнее изучать материал. Использование математического моделирования в проектной деятельности дает возможность применять математический аппарат для исследования различных процессов реальной жизни, осуществлять формализацию практических ситуаций в виде математических зависимостей и отношений, увидеть роль математики в будущей профессиональной деятельности. Кроме того, учитывая требования ФГОС ВО, при выполнении таких проектов студенты развивают творческие способности, навыки групповой коммуникации, техники публичных выступлений, формируют навыки использования научного стиля в письменной и устной речи.
Работа выполнена при финансовой поддержке ФГБОУ ВО «Шадринский государственный педагогический университет» по договору о выполнении НИР от 26.04.2018 г. № 145Н, а также при финансовой поддержке ФГБОУ ВО «Мордовский государственный педагогический институт имени М.Е. Евсевьева» по договору о выполнении НИР от 04.06.2018 г. № 1/338.
Библиографическая ссылка
Нигматулин Р.М., Вагина М.Ю. МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ В УЧЕБНЫХ ПРОЕКТАХ БАКАЛАВРОВ ПО ПРОФИЛЬНЫМ МАТЕМАТИЧЕСКИМ ДИСЦИПЛИНАМ // Современные наукоемкие технологии. 2018. № 10. С. 216-220;URL: https://top-technologies.ru/ru/article/view?id=37223 (дата обращения: 03.03.2026).