Статистические методы контроля и управления качеством широко применяются во всех отраслях промышленности. Благодаря широкому внедрению этих методов добились успеха японские, корейские, китайские корпорации. Еще раньше статистические методы применялись и применяются в странах Западной Европы и Северной Америки. Современное производство немыслимо без их использования.
Существующие методы статистического контроля и управления качеством, управления технологическим процессом основаны на предположении о наличии стабильного процесса, происходящего в постоянных условиях длительное время, возможности получить неограниченную выборку изделий и заготовок. Это положение с переходом на мелкосерийное, и тем более штучное, производство существенно меняется, и используемые стандартные методы статистических выводов перестают работать.
Основная проблема, возникающая при контроле малых выборок, заключается в существенном увеличении доверительных интервалов, поскольку их ширина пропорциональна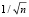 
, где n – объем выборки. Если точность оценок при n = 100 приблизительно равна 10 % (приблизительно потому, что в оценке ширины доверительного интервала присутствуют и другие множители), то при n = 10 – 32 %. Особенно существенны ошибки в оценке параметров при проведении контроля партий изделий по качественному признаку.
До настоящего времени эта проблема в математической статистике не разрешена, несмотря на большое количество работ в этой области.
Цель исследования: исследования С.В. Юдина и др. [1, 2] привели к выводу о необходимости разработки специальных методов контроля и управления качеством в случае мелкосерийного и штучного производства. Это связано с тем, что многие предприятия выпускают штучную и мелкосерийную продукцию, номенклатура которой постоянно меняется.
В монографии Д.В. Гаскарова и В.И. Шаповалова 1978 г. [3] впервые на высоком научном уровне рассмотрен вопрос об оценке параметров случайных чисел и проверки статистических гипотез по итогам данных, полученных при анализе малых выборок. Авторы использовали метод минимума энтропии и математический аппарат обобщенных функций. Они показали возможность при анализе малых выборок проводить оценки параметров распределений и даже проверку статистических гипотез, как о виде закона распределения, так и о наличии статистических связей.
Тем не менее точность оценок и доверительные вероятности, получаемые в результате предложенных методик, не могут быть применены в условиях высоких требований к изделиям ВВТ.
В 1989 г. была опубликована работа В.П. Савчука, посвященная байесовским методам статистического оценивания [4]. Эти методы основаны на важном принципе: информация меняет вероятности.
Целью исследования является разработка методов статистического приемочного контроля, основанного на гипергеометрическом распределении, учитывающие историю процесса с целью минимизировать риски при контроле малых партий.
Материалы и методы исследования
Формула Байеса уже давно, с конца XVIII века, применяется исследователями в самых разных областях, начиная с простых задач оценки вероятностей тех или иных событий на основе знаний о прошлом, заканчивая оценкой надежности сложных систем и построения систем искусственного интеллекта.
Уникальная формула Байеса имеет вид
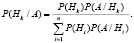(1)
Здесь A – наблюдаемое событие,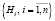 
– система гипотез.
Вероятности p(Hi) называются априорными (известными до опыта) вероятностями, а вероятности p(Hi/A) – апостериорными (полученными эмпирически после опыта) вероятностями.
Важнейшей проблемой в байесовском подходе является определение вероятностей, как события p(A), так и условных вероятностей p(Hi/A).
Данные вероятности могут быть определены только из длительных наблюдений за историей процесса. Чем дольше длится наблюдение, тем точнее наши оценки.
Следует отметить, что любые методы, основанные на использовании априорных вероятностей для исчисления апостериорных вероятностей, можно классифицировать как байесовские.
В работе [4] показано, что байесовский подход можно применять и в случае непрерывных распределений, причем многие оценки совпадают с теми же, найденными по принципу максимума энтропии.
Несмотря на важность этой работы для изучения возможностей байесовского подхода при оценке вероятностей интересующих нас событий и проверке статистических гипотез, в ней уделено очень мало внимания проблеме «малой выборки».
В 2008 г. в работе И.Е. Ишемгужина и др. [5] были рассмотрены критерии согласия для малой выборки при оценке надежности оборудования. Показано, что можно, применяя специальные критерии согласия, с достаточной надежностью идентифицировать закон распределения в задачах оценки надежности.
Недостатком этой статьи является недостаточная теоретическая проработка и отсутствие единого подхода в случае разных распределений.
Большая и теоретически важная работа Б.И. Сухорученкова 2010 г. по анализу малых выборок [6] содержит интересный авторский материал. К сожалению, в работе выборка объемом n = 30 считается малой. Для таких выборок нет нужды применять особые методы.
В работе М.П. Кривенко [7] используются информационная мера Кульбака – Лейблера, информация Фишера, параметрические и непараметрические статистические оценки в приложении к многомерным распределениям. Несмотря на важные теоретические результаты, практическое использование предложенных методов затруднено в связи со сложностью математического аппарата и тем, что в инженерной практике редко приходится использовать многомерные распределения.
В работах С.В. Юдина и др. [1, 2] на базе теории информации и байесовского подхода предложены новые методы, обладающие высокой надежностью, действительно применимые к анализу малых выборок, особенно в задачах оценки качества партии по данным выборки.
В статье С.В. Юдина [1] представлены основные теоретические положения нового подхода, основанные на знании априорной информации о качестве продукции и параметрах технологического процесса, а также концепции «интегрального риска».
Принцип интегрального риска и гипергеометрическое распределение
В работах [1, 2] был представлен принцип интегрального риска, который заключается в том, что при анализе процедуры статистического выборочного контроля учитываются интегральные вероятности принять партию с дефектностью, превышающей заданную (риск Потребителя b), или отклонить партию с дефектностью ниже граничной (риск Поставщика a).
Поскольку рассматриваемый ниже подход использует априорное распределение вероятности доли брака q на множестве контролируемых партий, то апостериорная вероятность интересующих контролера событий определяется с использованием обобщенного байесовского подхода.
При контроле партий малого объема, как правило, используется точное гипергеометрическое распределение числа дефектных изделий в выборке:
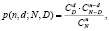(2)
где n – объем выборки; d – количество дефектных изделий в выборке; N – объем партии; D – количество дефектных изделий в партии.
Пусть с – приемочное число. Тогда оперативная кривая плана контроля, т.е. вероятность принять партию с количеством дефектов D, равна
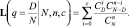(3)
При традиционном подходе риск Изготовителя (Поставщика) a определяется как вероятность забраковать партию с количеством дефектных изделий равных Dп:
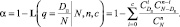(4)
Риск Потребителя b определяется как вероятность принять партию с количеством дефектных изделий Dб:
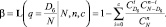(5)
Здесь Dп и Dб – приемочное и браковочное количества дефектных изделий в партии (Dп < Dб).
Недостатком этого подхода является точечность оценки, в то время как необходима интервальная оценка вероятности принятия бракованной партии. Потребителя, как правило, интересует общая вероятность принятия партии с неудовлетворительным уровнем дефектности, т.е. интегральный риск».
Результаты исследования и их обсуждение
Пусть известна гистограмма распределения дефектных изделий в партии, исходя из результатов исследований или результатов контроля партий в прошлом: fi (i = 0…N). Здесь fi – количество партий, в которых количество дефектных изделий равно i; N – объем партии. Пусть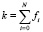 
– общее количество опытов. Тогда распределение вероятностей имеет вид 
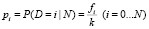. Пусть заданы интегральные риски Потребителя b и Поставщика a. Тогда для интегральных рисков имеем следующую систему уравнений:
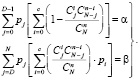(6)
Здесь D – предельно допустимое количество дефектных изделий в партии.
Система уравнений (6) дает возможность определить объем выборки n и приемочное число с, что определяет план контроля с заданными характеристиками.
Методика расчета гипергеометрических планов СПК на основе байесовского подхода
Входными данными для расчета оперативной кривой плана СПК, основанного на гипергеометрическом распределении, являются следующие числа: объем партии N; объем выборки n; предельно допустимое количество дефектных изделий в партии Dmax; приемочное число с.
Справочными числами являются риски изготовителя и потребителя.
На рис. 1 представлен скриншот листа MS Excel с расчетами.
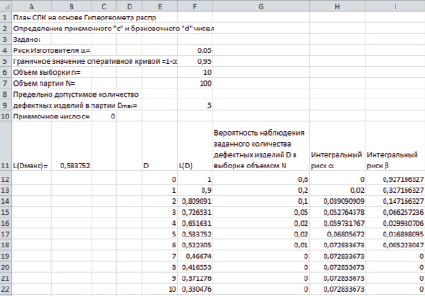
Рис. 1. Результаты расчетов в MS Excel
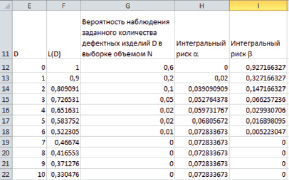
Рис. 2. Результаты расчета интегральных рисков
Пусть из истории наблюдений за готовыми изделиями известно распределение вероятности наблюдения заданного количества дефектных изделий D в выборке объемом N. Эти данные представлены в столбце ‘G’.
В столбцах ‘H’ и ‘I’ приведены результаты расчетов интегральных рисков Поставщика и Потребителя. Эти расчеты осуществлялись в соответствии с формулой.
На рис. 2 в большем масштабе представлены интересующие нас результаты.
Если исходить из предельно допустимого количества дефектных изделий в партии Dmax = 5, то в ячейке ‘H17’ интегральный риск a = 0,068 – это вероятность того, что будет забракована партия с количеством дефектных изделий 5 и менее; интегральный риск b = 0,005 (ячейка ‘I18’) – это вероятность того, что будет принята партия с числом дефектных изделий 6 и более.
Если установить оба риска равные 0,05, то с такой вероятностью мы забракуем партию с числом дефектных изделий 3 и меньше и примем партию с числом дефектных изделий 4 и более.
Представленный подход имеет широкую область применения, как в гражданской промышленности, так и на предприятиях ОПК.
Выводы
В результате проведенных исследований можно отметить, что использование байесовского подхода, базирующегося на принципе «информация меняет вероятности», а также концепции «интегрального риска», дает возможность с высокой точностью и надежностью оценить качество контролируемой партии, оценить риски, как Потребителя, так и Поставщика. Представлена методика расчета планов СПК, основанных на гипергеометрическом распределении, учитывающая историю работы предприятия.
Библиографическая ссылка
Юдин С.В., Протасьев В.Б., Подкопаев Р.Ю., Юдин А.С. МЕТОДИКА СТАТИСТИЧЕСКОГО ПРИЕМОЧНОГО КОНТРОЛЯ НА ОСНОВЕ БАЙЕСОВСКОГО ПОДХОДА (ГИПЕРГЕОМЕТРИЧЕСКОЕ РАСПРЕДЕЛЕНИЕ) // Современные наукоемкие технологии. – 2018. – № 10. – С. 161-165;URL: https://top-technologies.ru/ru/article/view?id=37213 (дата обращения: 19.04.2024).