В связи с активным переходом различных социальных сфер в формат среды данных, а также развитием средств по оказанию своевременной медицинской помощи независимо от территориальной локации актуальным становится ряд задач по созданию высокоэффективной системы телемедицины [1]. Создание регионального сегмента сети телемедицины, как и общей федеральной системы, требует рассмотрения важных аспектов, связанных в первую очередь со структурой (логической или физической топологией), выбором физической среды передачи данных, вопросами кибербезопасности и функционального назначения [2, 3]. В работе будет рассмотрен аспект, затрагивающий структурную организацию инфокоммуникационной сети телемедицины на примере Владимирской области. Цель работы – разработка математической модели инфокоммуникационной сети телемедицины для автоматизации процессов передачи данных и повышения эффективности её функционирования.
Организационная структура инфокоммуникационной сети телемедицины
Структурная организация, то есть непосредственная модель, описывающая и регламентирующая взаимодействие участников сеанса оказания медицинской услуги в удаленном режиме (врач – врач или врач – пациент), может быть реализована как одноранговая сеть, в которой все узлы функционально равноправны и каждый узел может связываться с любым другим непосредственно, и как иерархическая сеть [4], в которой сбор данных осуществляется в определённых узлах, данные дифференцируются по специфике обращения и перераспределяются на узлы другого структурного уровня. Одноранговая сеть (или точнее подсеть) телемедицины уже реализована во Владимирском регионе посредством телефонных линий связи для задач консалтинга в профессиональной среде врачей, однако для подключения нескольких специалистов (для решения, к примеру, неординарных случаев или при фронтальном обучении специалистов муниципального уровня) требуется централизация, и сеть перестает быть пиринговой. Регламентируется этот процесс положением, в котором прописан порядок обращения медицинских работников в случае необходимости консультирования. Взаимодействие врач – пациент наиболее эффективно реализуется в иерархической структуре взаимодействия. Представим данную сеть в виде графа связности узлов различного уровня (рис. 1), несложно заметить наличие самоподобия сети и фрактальный характер топологии [5]. Данные о состоянии человека начинают формироваться на уровне индивидуальной диагностики (рентгенологические снимки, УЗИ, магнитно-резонансные исследования – ранее сформированные данные, а также информация, полученная, например, в результате работы кардиостимуляторов – мгновенные данные) – это так называемый биометрический уровень. Далее, при необходимости либо в экстренном порядке, данные передаются в медицинское учреждение муниципального уровня, в котором перераспределяются: часть данных направляется к специалистам в пределах муниципального округа, часть – в региональный центр телемедицинской сети. На каждом уровне (биометрическом, муниципальном, региональном) требуется принимать решение об отправлении пакета данных на узел следующей иерархической ступени, что может осуществляться либо вручную, либо автоматически. Второй вариант предпочтительнее, поскольку уменьшает время на буферизацию и исключает человеческий фактор ошибки. Программы, осуществляющие автоматическое перераспределение информации, могут базироваться на способах индикации по ключевым словам, квалиметрическим оценкам по результатам диагностики, специальным маркерам, указанным на узле нижнего структурного уровня.
Математическая модель структурной организации сети
В качестве модели, отражающей такое устройство сети, может быть предложен ориентированный граф на множестве узлов биометрического, муниципального и регионального уровней (рис. 1). Для удобства дальнейшего представления присвоим каждой вершине графа числовое значение, а ребрам – соответствующее значение xj. Ориентированный граф (на карте региона уже определена своеобразная кластеризация по критерию муниципального деления) может быть задан процедурой роста некоторого эквидистантного множества eq(a, n), уровня n (n = 3), указывающего на структурный уровень сети [6]. Вектор v(ai, a) демонстрирует наличие связи между вершинами ai и a:
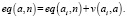(1)
Формируются координационные окружности eq(a, n), центры которых находятся в соответствующих вершинах a1, a2, a3. Цепь, заданную следующим образом [6]:
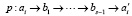, (2)
следует считать лучом, если выполняется условие, что расстояние между двумя вершинами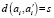 
является геодезическим. Выражения bi обозначают промежуточные узлы цепи от ai до 
.
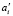Теперь для задания полного графа потребуется найти объединение всех лучей длины s, выходящих из вершин ai – p(ai, s)
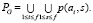(3)
Когерентные цепи такого графа удобно представить как
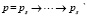(k – раз). (4)
а) б)
Рис. 1. Пример ориентированного графа сбора данных на примере территориального деления Владимирской области – а); топология самоподобного графа – б)
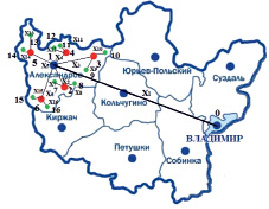
Рис. 2. Орграф на участке сети, демонтирующий связь на всех структурных уровнях
Автоматизация процесса передачи пакетов данных по такой сети может быть осуществлена на основе подхода кластеризации или заданием ориентированного графа сети, перестановки по которому образуют замкнутое множество относительно операции их бинарного умножения [7]. Продемонстрируем это на участке сети. Для простоты расчета выделим небольшой фрагмент сети, включающий взаимосвязь на уровнях Александров – Владимир. Зададим ориентированный граф графически (рис. 2).
Ориентированный граф, представленный семнадцатью вершинами и шестнадцатью ребрами, можно задать также с помощью матрицы инцидентности, определяющей структуру графа:
Столбцы в матрице соответствуют вершинам (с 0 по 16), а строки – ребрам. Веса элементов заданы в соответствии с правилом, по которому строится матрица инцидентности [8]:
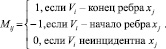
Перестановки на орграфе сети. Обсуждение результатов
Занумеруем вершины графа и зададим перестановки по графу следующим образом (рис. 2):
g[0] = (0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16); g[0] g[1] g[2] g[3]
g[1] = (0 0 1 1 1 1 1 2 2 3 3 4 4 5 5 6 6); g[1] g[2] g[3] g[3]
g[2] = (0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1); g[2] g[3] g[3] g[3]
g[3] = (0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0); g[3] g[3] g[3] g[3]
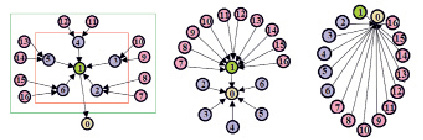
а) б) в)
Рис. 3. Визуализация структуры преобразований g[1] – a), g[2] – б), g[3] – в)
Визуализация престановок, представленная на рис. 3, позволяет заметить наличие у g[3] конвергентных свойств, поскольку орграф сходится в одной вершине (условно обозначенной за нулевую и соответсвующей узлу регионального центра), названной в работе [9] «римской точкой». Перестановки показывают, на каком структурном уровне аккумулируется информация и в какой узел она уже доставлена.
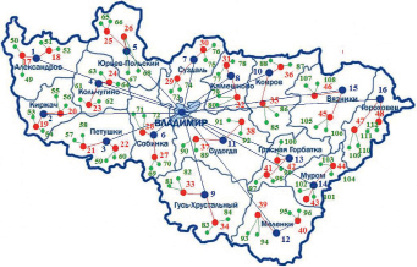
Рис. 4. Орграф региональной сети со 113 вершинами
Для графа, включающего большое число узлов, для прмера приведен граф на рис. 4, аналогичная процедура может быть осуществлена также компьютерными средствами перемоножения перестановок:
g[0] = (0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112)
g[1] = (0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 2 2 3 3 4 4 5 5 6 6 7 7 8 8 9 9 10 10 11 11 12 12 13 13 14 14 15 15 16 16 17 17 18 18 19 19 20 20 21 21 22 22 23 23 24 24 25 25 26 26 27 27 28 28 29 29 30 30 31 31 32 32 33 33 34 34 35 35 36 36 37 37 38 38 39 39 40 40 41 41 42 42 43 43 44 44 45 45 46 46 47 47 48 48)
g[2] = (0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 2 2 2 2 3 3 3 3 4 4 4 4 5 5 5 5 6 6 6 6 7 7 7 7 8 8 8 8 9 9 9 9 10 10 10 10 11 11 11 11 12 12 12 12 13 13 13 13 14 14 14 14 15 15 15 15 16 16 16 16)
g[3] = (0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0)
Таблица бинарного умножения для перестановок приведена ниже:
g[0] g[1] g[2] g[3]
g[1] g[2] g[3] g[3]
g[2] g[3] g[3] g[3]
g[3] g[3] g[3] g[3]
На модельном графе, включающем 113 узлов (0–112), за три этапа (что соответствует иерархическому разделению) пакеты данных доставляются в центральный узел (центр регионального консультирования), алгоритм перераспределения данных, базирующейся на перемножении перестановок по графу, позволяет ускорить и автоматизировать процесс обработки данных на отдельных узлах.
Выводы
В работе в качестве модели структурной организации региональной инфокоммуникационной сети телемедицины (на примере территориального деления во Владимирской области) предложен ориентированный граф. Показаны способы задания такого графа в виде объединения когерентных цепей, включающих в себя вершины, принадлежащие эквидистантному множеству (4), а также с помощью определения матрицы инцидентности. Перестановки на орграфе, а также операции их бинарного умножения позволяют задать алгоритм, автоматизирующий процесс сбора данных в узел регионального структурного уровня, а сами перестановки обладают конвергентными свойствами. Стоит отметить, что данный алгоритм, как и сам ориентированный граф, который он описывает, характеризуют процесс сбора данных в узел регионального уровня. Чтобы описать обратный процесс (к примеру, сообщение результатов заключения врача пациентам), требуется либо задавать уже неориентированный граф, либо создавать отдельную структуру (непосредственное доставление информации к пациенту, минуя уровни-медиаторы).
Библиографическая ссылка
Уланов Е.А., Горшков К.А., Никитин О.Р. МОДЕЛЬ РЕГИОНАЛЬНОЙ ИНФОКОММУНИКАЦИОННОЙ СЕТИ ТЕЛЕМЕДИЦИНЫ // Современные наукоемкие технологии. – 2018. – № 10. – С. 142-147;URL: https://top-technologies.ru/ru/article/view?id=37210 (дата обращения: 24.11.2024).