Для решения многих задач, традиционно считающихся творческими, используются интеллектуальные системы (ИС) [1, 2]. Опыт в таких системах хранится в виде базы знаний (БЗ), часто основанной на логической модели представления знаний [3]. В ней содержатся данные (факты), характеризующие объект (явление, событие) предметной области и отношения (правила), задающие связи между ними.
Одной из задач, для решения которых целесообразно применение ИС, является прогнозирование [4]. Процесс прогнозирования включает в себя сопоставление ожидаемого и наблюдаемого поведения объекта. Объект наблюдения в ходе своего развития переходит в новые состояния, каждое из которых может быть описано новыми фактами, поступающими в ИС. ИС на основе знаний о предметной области и объекте наблюдения, хранящихся в БЗ, а также новых поступивших фактов строит прогноз его дальнейшего возможного развития.
Составление прогноза с использованием дедуктивного вывода на определенном шаге может оказаться неуспешным по причине не полностью определенной БЗ, в которой отсутствуют некоторые факты. В таких условиях могут быть использованы правдоподобные рассуждения [3, 5, 6], в частности абдуктивный вывод [3, 7]. В статье [8] предложен метод вывода, который может быть использован для определения последующих возможных состояний объекта наблюдения из его текущего состояния. Однако, поскольку работа метода заключается в получении только уникальных следствий, то модель объекта не отражает возможность его перехода в предыдущие состояния. Вместе с этим формирование новых абдуктивных следствий осуществляется только при отсутствии новых дедуктивных, что приводит к потере возможных абдуктивных путей дальнейшего развития объекта. А отсутствие возможности задания глубины вывода не позволяет получить прогноз с требуемым периодом упреждения.
В случаях, когда необходимо представить в БЗ описание сложного объекта и его предметной области, или принимать решения в кратчайшие сроки на основе результатов вывода, требуется более наглядное объяснение хода рассуждений. Такое объяснение может быть получено с помощью схемы вывода.
Цель исследования: разработать метод логического вывода, решающий следующую задачу: при исходных посылках для новых фактов определить множества следствий, дополнительных фактов и описание схемы вывода, при этом множество исходных посылок, новых и дополнительных фактов непротиворечиво.
Формальная постановка задачи
Даны исходные непротиворечивые посылки M = {F1, …, FA, D1, …, DI} = MF ∪ MD и множество новых фактов MN = {N1, …, NB}, где MF - множество дизъюнктов-фактов; MD - множество дизъюнктов-правил. Задача формулируется следующим образом.
1. Определить семейства множеств дедуктивных sH = {e0, e1, …, eh, …, eH} и абдуктивных pH = {e'1, …, e'h, …, e'H} следствий, дополнительных фактов jH = {f1, …, fh, …, fH}. Сформировать общие множества следствий ME = e0 ∪ e1 ∪ … ∪ eH ∪ e'1∪ … ∪ e'H и дополнительных фактов MG = f1 ∪ … ∪ fH, при этом M ∪ MN ∪ MG совместно.
Множества следствий выводятся по формулам: e0 = MF ∩ MN; MN, M ⇒ e1;MN, M, f1 ⇒ e'1; MN, (ch ∪ c'h), M, gh ⇒ eh + 1;MN, (ch ∪ c'h), M, gh + 1 ⇒ e'h + 1. Здесь h = 1, …, H - 1 – шаг вывода; ch = ch-1 ∪ eh (c0 = e0) – полученные дедуктивные следствия; c'h = c'h-1 ∪ e'h ( c'0 = ∅) – полученные абдуктивные следствия; gh = gh-1 ∪ fh,gh + 1 = gh ∪ fh + 1 ( g0 = ∅) – полученные дополнительные факты.
2. Сформировать описание схемы вывода O = {z1, …, zh, …, zH} ∪ {e + }, где e + ⊆ ME – множество конечных следствий, из которых не выводятся новые следствия.
Материалы и методы исследования
Знания представлены в исчислении предикатов первого порядка. Факты, следствия – положительные литералы без аргументов-переменных. Правила – определенные хроновские дизъюнкты. Методы исследования основаны на обобщении результатов, полученных при построении процедур логического вывода следствий для знаний, представленных в исчислении высказываний.
Результаты исследования и их обсуждение
Описание схемы логического вывода следствий. Схема вывода – ориентированный граф, в котором вершины – секвенции, дуги – литералы. Введем обозначения: A – множество номеров исходных фактов; B – множество номеров новых фактов; C – множество имен литералов; I – множество номеров секвенций-правил; L – множество унифицирующих подстановок. Описание схемы S = {L[lij, ltk], L[lij, + ], L[ + , ltk], L[n, ltk], L[u, ltk] | L ∈ C; li, lt ∈ L; j, k ∈ I}, где j – номер секвенции, из вершины которой на схеме выходит, а k – номер секвенции, в вершину которой входит дуга, помеченная литералом L; « + » – символ вспомогательной переменной, определенной на I; n – символ нового факта; u – символ исходного факта. В описании схемы используются только положительные литералы.
Секвенции преобразуются в дизъюнкты следующим образом.
1. Литералы переносятся из левой части секвенции в правую.
2. Консеквенту назначается имя дизъюнкта в зависимости от вида секвенции (исходный факт Fa, новый факт Nb, исходное правило Di, где a ∈ A, b ∈ B, i ∈ I).
3. Литералам присваиваются параметры: L = L[u, + ] (Fa); L = L[n, + ] (Nb); 
L = L[ + , i], L = L[i, + ] (Di). Изначально l = q, где q - пустая подстановка, символ которой может быть опущен.
Например, секвенция-правило L1 & L2 > L3 преобразуется следующим образом: 1) 1 → L3 ∨ L1 ∨ L2; 2) Di = L3 ∨ L1 ∨ L2;3) Di = L3[i, + ] ∨ L1[ + , i] ∨ L2[ + , i]. Способ представления дизъюнкта Di на схеме вывода приведен на рис. 1, а.
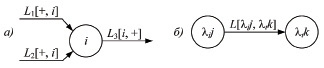
Рис. 1. Способ представления на схеме вывода: а) дизъюнкта Di , б) литерала L[λij, λtk]
Дуга, соединяющая на схеме вывода выход вершины lij с входом вершины ltk, помечается L[lij, ltk], который получается в результате «склеивания» L[lij, + ] и L[ + , ltk] (рис. 1, б). Склеивание – преобразование одноименных L[ + , k], L*[j, + ] в L[lj, lk] вследствие применения l. При построении схемы вершины с номерами lak и lbk считаются различными, если la ⊆ lb. Кроме того дуга L[lij, lak] соединяется с вершиной lbk, если la ⊆ lb.
Для осуществления логического вывода используется специальная операция обобщенного деления дизъюнкта.
Обобщенное деление дизъюнкта. Операцию обобщенного деления дизъюнкта b', содержащего La ∈ ba, на L*, результатом которой является частное a и остаток b'1, можно записать как b'[La] % L* = ⟨a, b'1⟩, где b' = ⟨ba, bc, b⟩ – дизъюнкт-делимое содержащий подстановку b, с помощью которой был получен антецедент ba и консеквент bc остатка-делимого; a – множество литералов, образующихся при склеивании La и L*; b'1 = ⟨ba 1, bc 1, b1⟩ – результирующий остаток, состоящий из антецедента ba 1 и консеквента bc 1 нового остатка-делимого и соответствующей ему подстановки b1 = b ∪ l.
Введем операцию объединения со склеиванием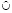 
. Ее результат – множество литералов, полученных объединением множеств и склеиванием. Например, {A(a, b)[1, + ], P(a, c)[5, + ]} 
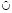{A(a, b)[1, 3]} = {A(a, b)[1, 3], P(a, c)[5, + ]}.
Остаток b'1 определяется по следующим правилам:
1) если a = ∅, то ba1 = 1, b1 = q, bc1 = 1;
2) если a ≠ ∅ и (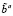
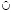a) - a = 
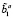= ∅, то ba1 = 0, b1 = b ∪ l, bc1 = b1bc;
3) если a ≠ ∅ и (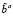
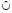a) - a = 
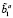≠ ∅, то ba1 = L1 ∨ … ∨ Ls ∨ … ∨ LS, b1 = b ∪ l,bc 1 = b1bc, где Ls ∈ 1 b?a .
Например, если b' = ⟨P(x, y)[ + , 1], O(y, x)[1, + ], q⟩, L* = P(b, a)[2, + ], то b'[P(x, y)[ + , 1]] % L* = ⟨a, b'1⟩, где a = {P(b, a)[2, {b/x, a/y}1]}, l = {b/x, a/y}, lP(x, y)[ + , 1] ∨ P(b, a)[2, + ] = P(b, a)[2, {b/x, a/y}1],b'1 = ⟨ba1, bc1, b1⟩. ba1 = 0, bc1 = b1bc = O(a, b)[1, + ], b1 = b ∪ l = q ∪ {b/x, a/y} = {b/x, a/y}, ⟨P(x, y)[ + , 1], O(y, x)[1, + ], q⟩ % P(b, a)[2, + ] = ⟨{P(b, a)[2, {b/x, a/y}1]}, ⟨0, O(a, b)[1, + ], {b/x, a/y}⟩⟩.
Процедура частичного деления. Опишем процедуру w = ⟨b', d, q, n, s, x⟩: d – остаток-делитель; q – признак возможности деления («0» – есть, «1» – нет, «2» – пустой остаток-делитель); n = {⟨b't, dt⟩ | t = 1, …, T} – множество новых пар остатков; s – множество дедуктивных следствий; x – множество литералов описания схемы вывода.
Определим «производную» дизъюнкта b'[La], содержащего La ∈ ba, по L*, через операцию обобщенного деления:
.
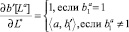Определим матрицу «производных» дизъюнкта b' по дизъюнкту d:
,
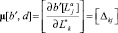где j = 1, …, J и k = 1, …, K, причем J – число литералов в дизъюнкте ba, а K – в дизъюнкте d.
В процедуре выполняются следующие действия.
1. Вычисляется μ[b', d], s = ∅, x = ∅. Если все Dkj = 1, то q = 1, n = {⟨b'1, 0⟩ | b'1 = b'},п. 5 (пункт 5), иначе q = 0.
2. L[bkji, + ] является дедуктивным следствием и включаются в s, если Dkj содержит bakj = 0 и L[i, + ] ∈ bсkj без аргументов-переменных.
3. В n = {⟨b't, dt⟩ | t = 1, …, T} включаются только пары, в которых bat ≠ 0. Если n = ∅, то q = 1, п. 4, иначе для b't вычисляется dt = d ÷ wt, где wt – дизъюнкт, содержащий исключаемые литералы. Из d исключаются L*k, для которых выполняется одно из условий: a) Dkj = 1, где j = 1, …, J; б) Dkj = 1, где j = 1, …, u, …, J, причем Dku = ⟨a, b't⟩. Если n содержит хотя бы один dt = 0, то q = 2.
4. Определяется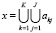 
.
5. Фиксируются результаты выполнения процедуры.
Процедура полного деления. Опишем процедуру W = ⟨D', d, u, Q, S, X, Y⟩:D' = ⟨Da, Dc, q⟩ – дизъюнкт посылки; d – выводимый дизъюнкт; u – вспомогательное множество, состоящее из ранее полученных фактов и следствий; Q – признак решения («0» – есть, «1» – нет); S – множество дедуктивных следствий; X – множество литералов описания схемы вывода; Y – множество конечных остатков. Остаток-делимое называется конечным, если он не имеет аргументов-переменных и его деление невозможно.
Введем операцию левоориентированного пересечения (объединения) множеств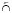 
(
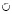). Ее результат – множество литералов, полученных пересечением (объединением) множеств и имеющих параметры одноименных литералов левого операнда. Например, {A(a, b)[1, + ], P(a, c)[5, + ]} 
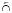{B(a, b)[2, + ], P(a, c)[7, + ]} = {P(a, c)[5, + ]}, {A(a, b)[1, + ], P(a, c)[5, + ]} 
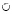{B(a, b)[2, + ], P(a, c)[7, + ]} = {A(a, b)[1, + ], B(a, b)[2, + ], P(a, c)[5, + ]}.
В процедуре используется индексная функция i(h) [4, 9] и выполняются следующие действия.
1. Выполняется w = ⟨D', d, q, n*, s, x⟩.Если q = 1, то S = s, X = x, п. 3. Если q ≠ 1, то сформированы новые пары остатков n* = {⟨b't, d*t⟩ | t = 1, …, T}. Образуется dt из *t t d? = d? ?? u . В n'0 включаются новые пары остатков ⟨b't, dt⟩ такие, что dt ≠ 0. Если n'0 = ∅, то S = s, X = x, п. 3, иначе h = 0, S0 = s, X0 = x.
2. Для каждой пары из n'h = {⟨b'i(h+1),di(h+1)⟩}, выполняется wi(h+1) = ⟨b'i(h+1), di(h+1), qi(h+1), ni(h+1), si(h+1), xi(h+1)⟩, где i(h + 1) = i(h).ti(h), ti(h) = 1, …, Ti(h). Пополняются 1 ( ). 1 V h h i h vS S s +== ?? и 1 ( ).1Vh h i h vvX X x +== ?? ,где v = ti(h), V = Ti(h). В n'h + 1 включаются новые b'i(h+2), di(h+2)⟩ такие, что di(h+2) ≠ 0. Если n'h + 1 = ∅, то S = Sh+1, X = Xh+1, п. 3, иначеh = h + 1, п. 2.
3. Выбираются конечные остатки из новых остатков-делимых Y = {y1, …, ya, …, yA},ya = L1[bi, + ] ∨ L2[ + , bi] ∨ … ∨ LJ[ + , bi].Если S = ∅ и Y = ∅, то Q = 1, X = ∅, п. 4, инче Q = 0 и в X сохраняются такие литералы,которые удовлетворяют условию: для каждого L[r, bcn] ∈ X существует L + [bmn, + ] ∈ S или L + [bmn, + ] ∈ ya такой, что bc ⊆ bm (здесь r – произвольный параметр). Если условие не выполняется, то L[r, bcn] исключается.Из X исключаются поглощаемые L[r, bcn] ⊆ L[r, bmn], когда bc ⊆ bm. В X добавляются Lj[ + , bi] из ya.
4. Фиксируются результаты выполнения процедуры.
Процедура вывода следствий. Перед выполнением метода задается максимальное число абдуктивных следствий на шаге вывода nmax = d. Чем меньше nmax, тем меньше логический вывод отличается от дедуктивного (nmax = 0). В то же время, чем больше nmax, тем больше будет получено следствий.
Опишем процедуру yh = ⟨MD, R, u, o,p, R1, f, z, nmax⟩: MD – множество исходных дизъюнктов-правил D'i = ⟨Dai, Dci, q⟩,Dai = L1[ + , i] ∨ … ∨ LJ[ + , i], Dci = L[i, + ];R = L1[r, + ] ∨ … ∨ LK[r, + ] – выводимый дизъюнкт; o = ⟨e, e'⟩ – пара дедуктивных e и абдуктивных e' следствий; p – признак возможности вывода («0» – есть, «1» – нет);R1 – новый выводимый дизъюнкт; f – множество дополнительных фактов; z – множество литералов описания схемы.
Процедура применима, если MD ≠ ∅ и Ji,K ≥ 1, иначе p = 1, e = e' = f = z = ∅, R1 = 0, п. 4.
1. Выполняются Wv = ⟨D'i, R, u, Qv, Sv,Xv, Yv⟩, где v = 1, …, V. Если все Qv = 1, тоp = 1, e = e' = f = z = ∅, R1 = 0, п. 4, иначе p = 0.
2. Формируется 
. В e' включаются не более nmax L[bi, + ] из Yv. В f включаются L[ + , bi] из Yv, если существует L + [bi, + ] ∈ e'.
3. В z включаются L[r, bci] из Xv для которых существует L[bmi, + ] в e ∪ e', где bc ⊆ bm. Формируется R1 из e ∪ e'.
4. Фиксируются результаты выполнения процедуры.
Метод логического вывода следствий. В методе выполняется y-процедура на каждом шаге h. Вывод завершается, если p = 1 или достигнуто заданное максимальное число шагов (h = H = g). Исходные литералы имеют вид: L[u, + ] для фактов базы; L[n, + ] для новых фактов; L[bih, + ], L[ + , bih] для правил.
В методе выполняются следующие действия.
1. Определяются начальные значения:h = 1, MD ≠ ∅, MN ≠ ∅, H = g, nmax = d.Формируется выводимый дизъюнкт R1 из MN. Определяются начальные множества: e0 = MF ? ?MN, s0 = {e0}, c1 = e0, p0 = ∅,c'1 = ∅, j0 = ∅, g1 = ∅, h0 = ∅, u1 = MF.
2. Выполняется yh = ⟨MD, Rh, uh, oh, ph, Rh + 1, fh, zh, d⟩.
3. Пополняются семейства множеств дедуктивных sh = sh-1 ∪ {eh} и абдуктивных ph = ph-1 ∪ {e'h} следствий, дополнительных фактов jh = jh-1 ∪ {fh}, описания схемы вывода hh = hh-1 ∪ {zh}. Если ph = 0 и h ≠ H, то вывод продолжается, h = h + 1, п. 4, иначе –завершается, п. 5.
4. Определяются множества дедуктивных c'h-1 ∪ e'h-1 следствий, дополнительных фактов gh = gh-1 ∪ fh-1,uh = MF ∪ MN ∪ ch-1 ∪ c'h-1 ∪ gh. При этом uhсодержит только L[u, + ]: в ch, c'h, gh вклю-чаются L[u, + ], полученные из L[bi, + ],L[ + , bi]; в uh включаются L[u, + ], полученные из L[n, + ] MN. Переход к п. 2.
5. Формируются общее множество следствий ME = e0 ∪ e1 ∪ … ∪ eH ∪ e'1 ∪ … ∪ e'H,общее множество дополнительных фактов MG = f1 ∪ … ∪ fH, описание схемы вывода следствий O = hH ∪ {e + }, где e + = (Z ? ? ME) - Z,Z = z1 ∪ … ∪ zH.
Построение схемы осуществляется в соответствии с шагами вывода. Вершины, из которых выходят дуги дедуктивных (абдуктивных) следствий, помечаются сплошной (пунктирной) линией. Расположенные на схеме вывода дуги фактов и конечных следствий не имеют исходных и заключительных вершин соответственно.
Применение метода к двум задачам приведено в [9].
Пример. Рассмотрим задачу о родственных связях [10]: отец (F) – персона (Per), родитель (P) мужского пола (m); дед (GF) – отец родителя; родные братья или сестры (S) – две различных (N) персоны с общим родителем; тетя (A) – персона, родная сестра родителя. Известно: Олег (с) – родитель Ирины (d); Светлана (b) – женщина (f). Новые факты: Олег – ребенок Михаила (a); Олег и Светлана – разные люди.
Формальное описание задачи: F1 = P(c, d)[u, + ], F2 = Per(b, f)[u, + ], D1 = F(x, y)[1, + ]∨ Per(x, m)[ + , 1] ∨ P(x, y)[ + , 1],D2 = GF(x, y)[2, + ] ∨ F(x, z)[ + , 2] ∨ P(z, y)[ + , 2 ] , D 3 = S ( x , y ) [ 3 , + ] ∨ P ( z , x )[ + , 3] ∨ P(z, y)[ + , 3] ∨ N(x, y)[ + , 3],D4 = A(x, y)[4, + ] ∨ Per(x, f)[ + , 4] ∨ P(z, y)[ + , 4] ∨ S(x, z)[ + , 4], N1 = P(a, c)[n, + ],N2 = N(b, c)[n, + ].
В результате получено описание O = {{P(a, c)[n, l111], Per(a, m)[ + , l111], N(b, c)[n, l231], P(a, c)[n, l231], P(a, b)[ + , l231]}, {F(a, c)[l111, l322], P(c, d)[u, l422], S(b, c)[l231, l542], P(c, d)[u, l642], Per(b, f)[u, l642]}, {GF(a, d)[l422, + ], A(b, d)[l642, + ]}} (рис. 2). Здесь l1 = {a/x, c/y}, l2 = {a/z, c/y, b/x}, l3 = {a/x, c/z}, l4 = {a/x, c/z, d/y}, l5 = {b/x, c/z}, l6 = {b/x, c/z, d/y}, при этом l3 ⊆ l4, l5 ⊆ l6.
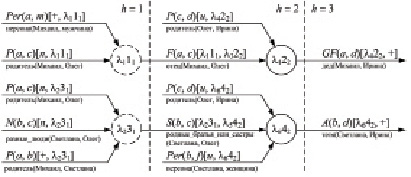
Рис. 2. Схема логического вывода следствий
Установлено, что (в случае, когда Михаил – мужчина Per(a, m)[ + , l111] и родитель Светланы P(a, b)[ + , l231]) Михаил – отец Олега (F(a, c)[l111, + ]), Олег и Светлана – родные брат и сестра (S(b, c)[l231, + ]), Михаил – дедушка Ирины (GF(a, d)[l422, + ]), Светлана – тетя Ирины (A(b, d)[l642, + ]).
Заключение
В работе предложен метод вывода следствий (дедуктивных и абдуктивных) с формированием описания схемы вывода в условиях неполной информации, обладающий следующими особенностями:
1) параллелизм при унификации литералов, формировании остатков и делении дизъюнктов;
2) независимый вывод всех следствий (дедуктивных и абдуктивных) на шаге, позволяющий сформировать все возможные пути дальнейшего развития объекта;
3) возможность перехода модели объекта в предыдущие состояния;
4) задание глубины вывода, позволяющее получать прогноз с требуемым периодом упреждения;
5) формирование описания схемы вывода, используемой в дальнейшем в качестве схемы прогнозирования для наглядного представления возможного развития объекта.
Особенности метода являются следствием его направленности на применение в задаче логического прогнозирования развития ситуаций из текущего состояния. Присущий методу многоуровневый параллелизм позволяет достаточно эффективно реализовать его в составе ИС на параллельных вычислительных платформах.
Библиографическая ссылка
Симонов А.И., Страбыкин Д.А. ВЫВОД СЛЕДСТВИЙ С ПОСТРОЕНИЕМ СХЕМЫ ВЫВОДА ИЗ НОВЫХ ФАКТОВ ПРИ НЕ ПОЛНОСТЬЮ ОПРЕДЕЛЕННОЙ БАЗЕ ЗНАНИЙ // Современные наукоемкие технологии. – 2018. – № 10. – С. 120-125;URL: https://top-technologies.ru/ru/article/view?id=37206 (дата обращения: 15.01.2025).