В настоящее время в России начались исследования, посвященные математическому моделированию эффективного воздействия средств массовой информации на человека [1, 2], моделированию психологии человека [3], исследованию воздействия СМИ на человека [4] на основе анализа поведения цифровых двойников, являющихся роботами с неабсолютной памятью [5, 6]. Необходимость проведения численных экспериментов, основанных на методах математического моделирования, обусловлена важностью прогнозирования результатов формирования общественного сознания [6, 7].
Для математического описания эффективного формирования воспитания роботов воспользуемся теорией математического анализа [8].
Пусть n – количество полных воспитательных циклов [5] трансляции передачи, mn – количество непрерывных трансляций передачи в воспитательном цикле с номером n, kn – количество пропущенных трансляций в этом же воспитательном цикле, θn – коэффициент памяти робота (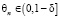
, 
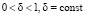) в полном воспитательном цикле с порядковым номером n, qn – элементарное воспитание (эмоциональное воздействие) у робота – цифрового двойника, возникшее в результате ознакомления с передачей в полном воспитательном цикле с порядковым номером n.
Согласно работе [5] формулу воспитания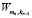 
цифрового двойника, полученного им в результате непрерывных трансляций mn в полном воспитательном цикле n, можем записать на основе соотношений
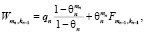
где
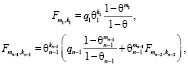(1)
Постановка задачи определения наибольшего воспитания цифрового двойника
С учетом равенств (1) можно сформулировать следующую задачу: «Найти количество полных воспитательных циклов, количество непрерывных воспитательных тактов и количество фиктивных тактов в каждом полном воспитательном цикле, обеспечивающих наибольшее воспитание робота при завершении воспитания».
Последняя фраза математически описывается следующим образом:
найти
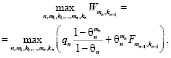(2)
Пусть выполняются допущения
, 
, 
,
, 
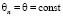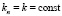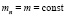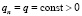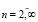. (3)
В этом случае задача (2) эквивалентна следующей задаче:
найти
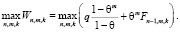(4)
Так как справедливо соотношение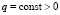 
, то задачу (3) можно записать в следующем виде:
найти
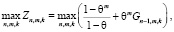(5)
где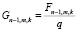 
, то есть
,
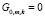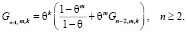
Решение оптимизационной задачи
Так как при выполнении условий (3) последовательность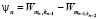 
является монотонно возрастающей [5], то зафиксируем произвольное значение n и определим величины m и k, обеспечивающие 
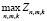при этом фиксированном n ≥ 2.
Нетрудно доказать справедливость формулы
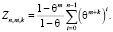(6)
Согласно равенству (6) можно сделать вывод о том, что большему значению коэффициента памяти θ, если робот является равномерно забывчивым с равноценными эмоциями, соответствует большее воспитание, полученное в результате воздействия на него равными полными воспитательными циклами, причем чем больше количество этих циклов, тем больше воспитание робота.
Нетрудно заметить, что соотношение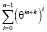 
является частичной суммой геометрической прогрессии со знаменателем 
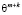. Частичная сумма 
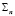этой геометрической прогрессии определяется формулой
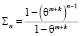, (7)
где n ≥ 2.
С учетом (7) равенство (6) примет вид
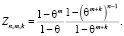(8)
Анализируя формулу (8), можно сделать вывод о том, что, чем больше фиктивных тактов в равных полных воспитательных циклах, тем меньше воспитание робота. Согласно соотношению (8) справедливы свойства
,
.
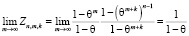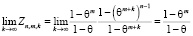Перейдя к пределу при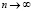 
в равенстве (8), получим соотношение
.
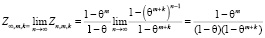Таким образом, предельное воспитание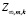 
равномерно забывчивого робота с равноценными эмоциями описывается формулой
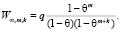
В силу того, что последовательность Zn,m,k является положительной и монотонно возрастающей по параметру n, справедливо соотношение
.
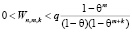Сформулируем и докажем ряд теорем.
Теорема 1. Если функции f(x) и g(x) положительны и являются монотонно возрастающими, то функция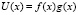 
монотонно возрастающая.
Доказательство.
Справедливо соотношение
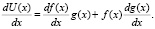
Так как в силу условий теоремы 1 справедливы неравенства
,
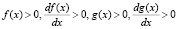то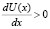 
, а поэтому 
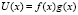является монотонно возрастающей функцией.
Теорема доказана.
Теорема 2. Функция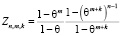 
является монотонно возрастающей по параметру m.
Доказательство.
Пусть функция f(m) удовлетворяет соотношению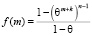 
, а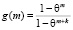 
.
Тогда справедливо равенство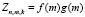 
.
Легко видеть, что функция f(m) является положительной и монотонно возрастающей.
Также очевидна справедливость неравенства g(m) > 0.
Покажем, что функция g(m) является монотонно возрастающей.
Несложные преобразования позволяют получить формулу
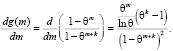
Так как справедливо неравенств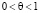о 
, то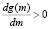 
, то есть функция g(m) монотонно возрастающая.
А следовательно, в силу свойств функции f(m) согласно теореме 1 функция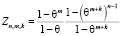 
является монотонно возрастающей по параметру m.
Теорема доказана.
Теорема 3. Функция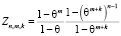 
монотонна по параметру k, начиная с некоторого порядкового номера 
, где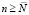 
.
Доказательство.
Представим функцию Zn,m,k в виде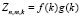 
, где функция f(k) удовлетворяет соотношению 
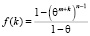, а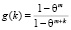 
.
Согласно формуле производной от произведения функций справедлива цепочка соотношений
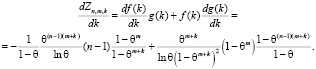(9)
Пусть
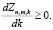(10)
После несложных преобразований соотношения (9) нетрудно показать, что справедливость неравенства (10) определяется справедливостью формулы
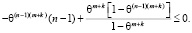(11)
Перейдем в обеих частях соотношения (11) к пределу при 
, тогда получим
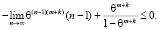(12)
Очевидна цепочка соотношений
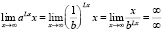, (13)
если выполняются неравенства L ≥ 1 и b ≥ 1.
Раскроем неопределенность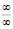 
в соотношении (13) по правилу Лопиталя [4], тогда получим
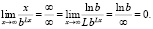(14)
Пусть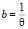 
, x = n –1, L = m + k, тогда согласно формуле (14) соотношение (12) примет вид
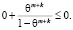(15)
Однако при фиксированных положительных значениях m и k справедливо строгое неравенство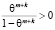 
, поэтому с учетом соотношения (15) получаем: 0 > 0, то есть справедлива формула 
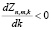, а значит, функция Zn,m,k является монотонно убывающей по параметру k, начиная с некоторого порядкового номера 
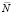, где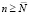 
.
Теорема доказана.
Исходя из анализа доказанного свойства монотонного убывания функции Zn,m,k по параметру k, можно заключить, что одним из оптимальных параметров решения задачи (5) будет k = 1.
Таким образом, с учетом (8) целевая функция задачи (5) примет вид
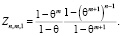(16)
Заключение
Таким образом, решением задачи (5) являются наибольшие значения n и m, обусловленные возможностями практики, и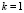 
. Иными словами, этот вывод можно сформулировать следующим образом: «Для получения наибольшего воспитания робота – цифрового двойника с помощью средств массовой информации достаточно в полных воспитательных циклах после непрерывных трансляций передач медиа-проекта делать не более одного пропуска передач».
Библиографическая ссылка
Пенский О.Г., Ощепкова Н.В. МАТЕМАТИЧЕСКИЕ МОДЕЛИ ВОСПИТАНИЯ РОБОТОВ С ПОМОЩЬЮ СРЕДСТВ МАССОВОЙ ИНФОРМАЦИИ // Современные наукоемкие технологии. – 2018. – № 10. – С. 98-102;URL: https://top-technologies.ru/ru/article/view?id=37202 (дата обращения: 24.11.2024).