Биоинспирированные алгоритмы – активно развивающаяся область методов оптимизации и принятия решений. На данный момент наиболее перспективным направлением следует считать создание новых версий биоинспирированных алгоритмов, учитывающих проблемно-ориентированную информацию об области поиска оптимальных решений, а также предысторию поиска. Для создания новых высокоэффективных биоинспирированных алгоритмов используется такой метод, как гибридизация. Гибридные биоинспирированные алгоритмы в процессе своего развития могут избавиться от основных недостатков классических биоинспирированных алгоритмов.
Цель исследования: научная новизна исследования заключается в разработке гибридного биоинспирированного алгоритма поиска оптимальных значений, основанного на работе двух совмещенных метаэвристических алгоритмов, при этом без потери их положительных свойств, но с избеганием их недостатков.
Нельзя не отметить, что количество допустимых решений огромно, чаще всего метаэвристические методы дают возможность реализовывать поиск близких к наилучшим решениям с минимальными вычислительными затратами, в отличие от оптимизационных задач, которые решены традиционным способом [1].
Материалы и методы исследования
Для последующей гибридизации были выбраны два алгоритма: алгоритм роя частиц и алгоритм имитации отжига, а также рассмотрены их сильные стороны и недостатки.
В последние годы всё большее применение при решении различных прикладных задач оптимизации находит алгоритм роя частиц, предложенный в 1995 г. Дж. Кеннеди и Д.К. Эберхартом в качестве алгоритма оптимизации непрерывных нелинейных функций.
Алгоритм оптимизации роя частиц имитирует социальное поведение стаи птиц, косяка рыб. Начиная свою работу на наборе случайно распределенных частиц (потенциальных решений), алгоритм пытается улучшить решения в соответствии с некоторой мерой качества (фитнессфункцией, функцией пригодности). Импровизация выполняется путем перемещения частиц вокруг пространства поиска с помощью набора простых математических выражений, которые моделируют некоторые связи между частицами. Эти математические выражения в их простейшей и самой обычной форме предполагают движение каждой частицы к ее самому лучшему опытному положению, а также к лучшему положению роя, наряду с некоторыми случайными возмущениями. Однако существует множество вариантов, которые используют различные правила обновления значений алгоритма [2].
Одним из основных преимуществ алгоритма роя частиц является его способность относительно быстро находить достаточно хорошие решения. В то же время — это, вероятно, самый признанный недостаток алгоритма. Хотя алгоритм роя частиц обнаруживает качественные решения намного быстрее, чем эволюционные алгоритмы, он не улучшает качество решений по мере увеличения количества поколений. Это связано с тем, что частицы сосредоточены в небольшой области поискового пространства и, следовательно, теряют разнообразие [3].
Гибридизация алгоритма роя частиц с другими биоинспирированными алгоритмами является одной из самых популярных стратегий. Это связано главным образом с тем, что полученный алгоритм сохраняет положительные характеристики метаэвристических алгоритмов, таких как возможность глобального поиска, небольшая зависимость от начальной точки, отсутствие необходимости в информации о градиенте и применимость к негладким или невыпуклым областям поиска. Другой биоинспирированный алгоритм, который может быть успешно гибридизирован с алгоритмом, может быть представлен как отдельным агентом, так и популяцией.
В данной работе предлагается реализовать комбинационный способ повышения эффективности базового алгоритма роя частиц посредством разработки его гибридных версий с применением алгоритма имитации отжига (ИО).
Алгоритм имитации отжига основан на аналогии взятой из термодинамики, которая заключается в следующем: для выращивания кристалла мы начинаем нагревать материал до тех пор, пока он не достигнет его расплавленного состояния. Затем постепенно уменьшаем температуру до образования кристаллической структуры. Стандартная процедура алгоритма ИО начинается с генерации исходного решения случайным образом. На начальных этапах делается небольшое случайное изменение в текущем решении. Затем вычисляется целевое значение функции нового решения и сравнивается с целевой функцией текущего решения. Выполняется переход к новому решению, если он имеет лучшее значение функции или если функция вероятности, реализованная в алгоритме ИО, имеет более высокое значение, чем случайное число. В противном случае создается и оценивается новое решение [4].
Расчет функции вероятности основан на параметре температуры, поскольку он играет аналогичную роль в процессе физического отжига. Чтобы избежать попадания в локальную точку минимума, скорость снижения должна быть медленной. Таким образом, в начале работы алгоритма ИО могут быть приняты самые худшие варианты, но в конечном итоге будут допущены только лучшие, что должно помочь алгоритму выскочить из локального минимума. Алгоритм может быть прерван после того, как определенная часть объема задачи была достигнута или после заданной продолжительности выполнения.
Чтобы избежать преждевременной конвергенции алгоритма роя частиц, предлагаем использовать гибридный биоинспирированный алгоритм, основанный на том, что алгоритм роя частиц обеспечивает быструю сходимость, в то время как алгоритм имитации отжига обеспечивает поиск локальных оптимумов из-за его сильной локально-поисковой способности [5].
Этот гибридный подход в полной мере использует возможности как алгоритма роя частиц, так и алгоритма ИО и компенсирует слабые стороны каждого из них. Следовательно, предложенный гибридный алгоритм способен выходить из локального оптимума. Однако если алгоритм ИО применяется к алгоритму РЧ на каждой итерации, то вычислительная стоимость резко возрастет, и, соответственно, способность к быстрой сходимости алгоритма теряет свои преимущества. Для гибкой интеграции, алгоритм имитации отжига применяется к алгоритму роя частиц каждые ???? итераций, если не происходит улучшения глобального оптимума. Таким образом, данный гибридный подход способен поддерживать большую часть времени быструю сходимость алгоритма благодаря преимуществам алгоритма роя частиц и избегать локального оптимума с помощью особенностей алгоритма имитации отжига.
Блок-схема данного гибридного алгоритма представлена на рис. 1.
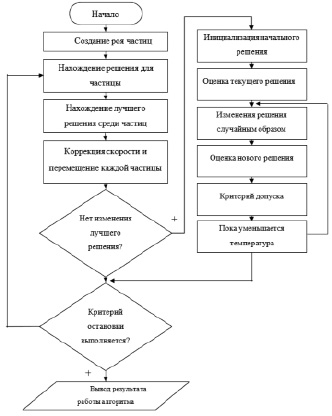
Рис. 1. Блок-схема гибридного алгоритма
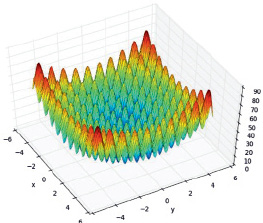
Рис. 2. График функции Растригина
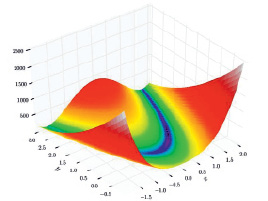
Рис. 3. График функции Розенброка
Была произведена программная реализация гибридного алгоритма. Тестирование гибридного алгоритма оптимизации проходило с применением двух тестовых функций: функции Растригина и функции Розенброка.
Функция Растригина имеет вид
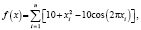
где n = 2;
x1∈[–5,12, 5,12], x2∈[–5,12, 5,12].
Точка глобального минимума функции находится по координатам [0, 0], а функция принимает значение fmin = 0.
Функция Розенброка имеет вид
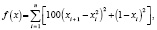
где n = 2;
x1∈[–30, 30], x2∈[–30, 30].
Точка глобального минимума функции находится по координатам [1, 1], а функция принимает значение fmin = 0.
Результаты исследования и их обсуждение
В ходе проведения исследования работы алгоритма на двух тестовых функциях было реализовано по 100 тестовых запусков алгоритма, при условии, что в рамках одного запуска поиск глобального оптимума проходил до момента достижения максимального числа итераций работы алгоритма или достижения достаточной точности при нахождении наилучшего значения оптимума, которая составляет 0.0000001.
Оценка эффективности работы алгоритмов будет проведена, основываясь на следующие параметры, вычисленные как среднее арифметическое от всех тестовых запусков алгоритма:
1. Среднее время работы алгоритма. Это время в секундах от начала работы алгоритма до момента нахождения первого глобального оптимума, который удовлетворяет достаточной точности.
2. Средняя скорость поиска. Это количество итераций, которые понадобились алгоритму для нахождения первого глобального оптимума, который удовлетворяет достаточной точности.
3. Среднее значение целевой функции. Это значение функции в точке первого глобального оптимума, который удовлетворяет достаточной точности.
В каждом из проведенных испытаний работы гибридного алгоритма оптимизации на целевых функциях был применен одинаковый набор параметров, указанный в табл. 1.
В результате программного тестирования гибридного алгоритма была сформирована табл. 2. Эксперимент прошел успешно, фатальных ошибок не обнаружено, каждый запуск работы гибридного алгоритма оптимизации давал результат.
Таблица 1
Начальный набор параметров
|
Количество поколений |
1000 |
|
Размер популяции роя частиц |
100 |
|
Размерность пространства поиска |
2 |
|
Начальная температура системы |
10 |
|
Коэффициент охлаждения |
0,99 |
|
Коэффициент инерции частиц |
0,8 |
|
Радиус пространства поиска соседних решений |
3 |
Выводы
Из табл. 2 видно, что предложенная гибридная комбинация алгоритмов показывает хорошие результаты. Стоит отметить, что разработанный алгоритм показывает наилучшую скорость и время сходимости на функции Растригина.
Таблица 2
Результаты экспериментального тестирования
|
Функция |
Среднее время сходимости, с |
Средняя скорость сходимости |
Среднее значение целевой функции |
|
Розенброка |
0,00855 |
861,6 |
8,51403858760999e-7 |
|
Растригина |
0,00446 |
277,57 |
5,345056166561335e-8 |
Полученные экспериментальные результаты программного тестирования позволяют с уверенностью заявить об эффективности гибридного алгоритма, основанного на комбинации методов роя частиц и имитации отжига, в решении оптимизационных задач со спецификой целевой функции.
Разработанный гибридный подход был применён к оптимизации тестовых целевых функций: Растригина и Розенброка. Полученные экспериментальные результаты программного тестирования показали высокую эффективность нового гибридного алгоритма, основанного на комбинации методов роя частиц и имитации отжига, в решении оптимизационных задач со спецификой целевой функции.
Статья написана при поддержке гранта РФФИ № 16-01-00391 «Разработка комбинированных алгоритмов для решения распределительных и транспортных задач с использованием идеологии искусственных иммунных систем и биоинспирированных алгоритмов».
Библиографическая ссылка
Остроух Е.Н., Требухин А.В., Чернышев Ю.А., Панасенко П.А. РАЗРАБОТКА И АНАЛИЗ ГИБРИДНОГО АЛГОРИТМА РЕШЕНИЯ НЕЛИНЕЙНЫХ ЗАДАЧ ОПТИМИЗАЦИИ // Современные наукоемкие технологии. 2018. № 10. С. 87-91;URL: https://top-technologies.ru/ru/article/view?id=37200 (дата обращения: 03.03.2026).



