Задача обеспечения нормального теплового режима электронного аппарата относится к одной из важнейших задач его проектирования. Способы обеспечения требуемого теплового режима подразделяются на активные и пассивные. Активные способы предполагают использовать системы охлаждения с тем или иным теплоносителем, позволяющим переносить тепловую энергию от источников тепла к теплостоку. В пассивных способах обеспечения теплового режима электронных аппаратов имеют место следующие механизмы:
- использование элементов конструкций с хорошей теплопроводностью;
- использование при установке элементов специальных теплопроводных паст для снижения теплового контактного сопротивления;
- снижение энергопотребления за счет динамического управления питанием микросхем в зависимости от их работы или простоя;
- рациональное размещение источников тепла в электронных аппаратах.
Обеспечение оптимального теплового режима без использования активных систем охлаждения позволяет уменьшить весогабаритные характеристики электронных аппаратов, а в некоторых случаях снизить их стоимость.
Пассивные способы наиболее актуальны при обеспечении требуемого теплового режима для электронных аппаратов с жесткими ограничениями на весогабаритные характеристики и специфическими условиями эксплуатации, например невесомость, вакуум.
Оптимизация теплового режима путем рационального размещения источников тепла позволяет снизить температуру электронных элементов, что повышает надежность электронных аппаратов, поскольку она существенно зависит от их рабочей температуры [1–5]. Учет тепловых факторов в задаче размещения добавляет еще один критерий, и задача усложняется. Поэтому очень важно оценить: какой потенциал имеется для улучшения теплового режима. Если перспективы улучшения теплового режима слабые, то нет необходимости учитывать тепловые критерии в задаче размещения.
В [6] предложен критерий для оценки перспектив улучшения теплового режима путем рационального размещения электронных элементов. Недостаток этого критерия заключается в том, что он не учитывает характер распределения тепловых сопротивлений от посадочных позиций электронных элементов до теплостока и может неадекватно оценивать ситуацию в некоторых случаях. Например, в случае, когда условия теплоотвода от посадочных позиций мало отличаются между собой, этот критерий может предсказать хорошие перспективы, так как он ориентируется только на характер распределения мощностей электронных элементов. А это будет неверно, так как в этом случае никаких перспектив нет.
Цель исследования: в данной работе предлагается новый критерий, позволяющий с хорошей точностью оценить перспективы улучшения теплового режима путем рационального размещения электронных элементов на плате, установленной в микроблоке электронной аппаратуры. Адекватность предложенного критерия обосновывается теоретически и подтверждается практически путем проведения вычислительного эксперимента.
Материалы и методы исследования
Для вычисления критерия используются параметры тепловой модели, реализующей принцип суперпозиции температурных полей [7]:
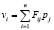 ,
,
где vi – перегрев i-й части системы относительно окружающей среды (теплостока); Fij – тепловой коэффициент влияния j-той области на i-ю; pj – мощность, рассеиваемая j-й областью системы; n – число характерных областей, из которых состоит система.
Для оценки перспектив улучшения теплового режима за счет рационального размещения электронных элементов предлагается использовать следующий критерий:
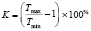 ,
,
где 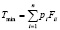 ;
;
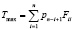 ;
;
{p1, p2, p3,..., pn} – множество упорядоченных по невозрастанию мощностей рассеивания электронных элементов;
{F11, F22, F33,…, Fnn} – множество упорядоченных по неубыванию тепловых коэффициентов.
Будем считать, что количество электронных элементов n равно количеству посадочных позиций. Случаи, когда посадочных позиций больше, чем электронных элементов, легко свести к принятому допущению, считая мощности рассеяния недостающих элементов нулевыми (добавить недостающее количество элементов с нулевой мощностью рассеивания).
С физической точки зрения коэффициент Fii представляет собой тепловое сопротивление от посадочной позиции до теплостока. Физический смысл произведения piFjj – это собственный перегрев электронного элемента с мощностью pi, установленного на посадочную позицию j.
Таким образом, вычисляется сумма собственных перегревов электронных элементов для их оптимального размещения Tmin (оптимистичное значение) и для неоптимального размещения Tmax (пессимистичное значение).
Нетрудно доказать, что всегда будет соблюдаться неравенство: Tmax ≥ Tmin. Для этого нужно доказать, что перестановка любых двух электронных элементов не уменьшит Tmin и не увеличит Tmax. Допустим, что в выражении для Tmin переставили элементы pi и pj. Тогда получим
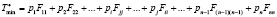 .
.
Теперь найдем разность:
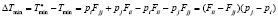 .
.
В силу того, что тепловые коэффициенты упорядочены по неубыванию, а мощности рассеивания – по невозрастанию, результаты в скобках (Fii – Fjj) и (pj – pi) будут иметь одинаковые знаки, либо результат их перемножения может быть равным нулю, при условии Fii = Fjj или pj = pi или pj = pi = 0. Из проведенного анализа следует, что ΔTmin ≥ 0, то есть любая перестановка электронных элементов не может уменьшить Tmin.
Аналогичное доказательство можно привести и для Tmax, то есть любая перестановка электронных элементов не может увеличить Tmax.
Можно поставить также задачу: при каком характере распределения мощностей может быть достигнуто максимальное значение критерия K. При этом подразумевается, что суммарная мощность рассеивания электронных элементов – величина неизменная. Для этого необходимо решить две задачи линейного программирования (1), (2):
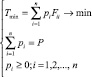 , (1)
, (1)
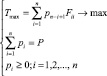 . (2)
. (2)
Эти задачи легко решаются с помощью надстройки «найти решение» приложения Excel. Решение этих задач даст нам минимально возможное значение min(Tmin) и максимально возможное max(Tmax) при неизменной суммарной мощности рассеивания электронных элементов. Теперь можно вычислить максимально возможное значение критерия Kmax:
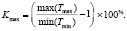
Выбор для оценки перспектив оптимизации теплового режима критерия K легко обосновать тем, что собственные перегревы непосредственно формируют температурное поле, а критерий фактически указывает, в каких пределах возможно снизить перегревы.
Для проверки теоретических исследований проведем вычислительный эксперимент. Объектом исследования выбрана печатная плата, а областями являются посадочные позиции, имеющие мощности рассеивания установленных в них источников тепла, представляющих собой интегральные схемы. В работе [7] рассмотрена технология вычисления тепловых коэффициентов. Воспользуемся её результатами, полученными для платы с 24 посадочными позициями и радиальным теплоотводом. Плата с позициями, пронумерованными в порядке неубывания тепловых коэффициентов Fii(i = 1,2,…,24), представлена на рис. 1. Для удобства пронормируем значения тепловых коэффициентов относительно максимальной величины. Это не повлияет на значения критерия K.

Рис. 1. Нумерация посадочных позиций на плате
После нормализации будем иметь следующие значения тепловых коэффициентов:
F11 = F22 = F33 = F44 = 0,79;
F55 = F66 = F77 = F88 = 0,82; F99 = F10,10
= = F11,11 = F12,12 = 0,84;
F13,13 = F14,14 = F15,15 = F16,16 = 0,87; F17,17 =
= F18,18 = F19,19 = F20,20 = 0,98; F21,21 =
= F22,22 = F23,23 = F24,24 = 1,0.
Для проведения вычислительного эксперимента были выбраны следующие значения мощностей рассеивания в ваттах:
p1 = p2 = p3 = p4 = 0,17; p5 = p6 = p7 = p8 = 0,15;
p9 = p10 = p11 = p12 = 0,12; p13 = p14 = p15 = p16 = 0,1;
p17 = p18 = p19 = p20 = 0,08;
p21 = p22 = p23 = p24 = 0,06.
В качестве инструментального средства для расчета тепловых режимов применена подсистема расчета тепловых режимов микроблоков электронной аппаратуры, использованная в работе [7].
Результаты исследования и их обсуждение
Вычислим сначала значение критерия для принятых исходных данных:
K = (( p24F11 + p23F22 + p22F33 + p21F44 + p20F55 +
+ p19F66 + p18F77 + p17F88 + p16F99 + p15F10,10 +
+ p14F11,11 + p13F12,12 + p12F13,13 + p11F14,14 +
+ p10F15,15 + p9F16,16 + p8F17,17 + p7F18,18 + p6F19,19 +
+ p5F20,20 + p4F21,21 + p3F22,22 + p2F23,23 + p1F24,24)/
(p1F11 + p2F22 + p3F33 + p4F44 + p5F55 + p6F66 + p7F77 +
+ p8F88 + p9F99 + p10F10,10 + + p11F11,11 + p12F12,12 +
+ p13F13,13 + p14F14,14 + p15F15,15 + p16F16,16 + p17F17,17 +
+ p18F18,18 + p19F19,19 + p20F20,20 + p21F21,21 +
+ p22F22,22 + p23F23,23 + p24F24,24) – 1)×100 % = 5,98 %.
Критерий показывает, что улучшение теплового режима возможно в пределах 5,98 %.
Теперь проведем расчеты с помощью подсистемы расчета тепловых режимов для случая оптимального и неоптимального размещения элементов. Результаты представлены в таблице.
Подсчитаем разницу средних значений перегревов для оптимального и неоптимального размещения в процентах относительно теплостока, температура которого tтеплостока = 25 градусов:
Δυ = ((υсред. неоптим./ υсред. оптим) – 1)×100 % = ((16,53/15,58) – 1)×100 % = 6,09 %,где υсред. неоптим. = tсред. неоптим. – 25; υсред. оптим. = tсред. оптим – 25; tсред – средняя температура.
Экспериментальные расчеты показывают незначительные отличия возможностей улучшения теплового режима за счет рационального размещения электронных элементов от результатов, определяемых по предложенному критерию K. Разница в районе полпроцента вписывается в погрешности расчета. На рис. 2 показан график, отражающий изменение температуры посадочных позиций для оптимального и неоптимального размещения электронных элементов.
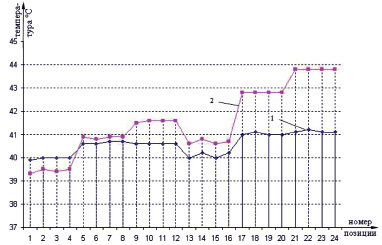
Рис. 2. Температура позиций для оптимального – 1 и неоптимального – 2 размещения
Решение задач (1) и (2) при неизменной суммарной мощности электронных элементов позволило вычислить Kmax:
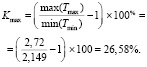
Расчет тепловых режимов, для случая распределения мощностей рассеивания, соответствующего Kmax, дал следующий результат: разница средних значений перегревов для оптимального и неоптимального размещения в процентах относительно теплостока составила 29,68 %. Это результат близкий к Kmax = 26,58 %. Здесь следует отметить, что решения задач (1) и (2) дают нереальный результат распределения мощностей, то есть вся мощность рассеивания сосредоточена в одном электронном элементе, хотя такая ситуация на практике не может возникнуть.
Расчеты с помощью подсистемы расчета тепловых режимов для случая оптимального и неоптимального размещения элементов
|
Оптимальный вариант |
Неоптимальный вариант |
Номер посадочного места |
|
|
Температура посадочных позиций (оС) |
39,9 |
39,3 |
1 |
|
40,0 |
39,5 |
2 |
|
|
40,0 |
39,4 |
3 |
|
|
40,0 |
39,5 |
4 |
|
|
40,6 |
40,9 |
5 |
|
|
40,6 |
40,8 |
6 |
|
|
40,7 |
40,9 |
7 |
|
|
40,7 |
40,9 |
8 |
|
|
40,6 |
41,5 |
9 |
|
|
40,6 |
41,6 |
10 |
|
|
40,6 |
41,6 |
11 |
|
|
40,6 |
41,6 |
12 |
|
|
40,0 |
40,6 |
13 |
|
|
40,2 |
40,8 |
14 |
|
|
40,0 |
40,6 |
15 |
|
|
40,2 |
40,7 |
16 |
|
|
41,0 |
42,8 |
17 |
|
|
41,1 |
42,8 |
18 |
|
|
41,0 |
42,8 |
19 |
|
|
41,0 |
42,8 |
20 |
|
|
41,1 |
43,8 |
21 |
|
|
41,2 |
43,8 |
22 |
|
|
41,1 |
43,8 |
23 |
|
|
41,1 |
43,8 |
24 |
Были проведены также расчеты для случая решения задач (1) и (2) с введением дополнительных ограничений: pi ≥ pmin; pi ≤ pmax (i = 1,2,…,24). В нашем эксперименте pmin = 0,06 вт, pmax = 0,17 вт. При этом получили результат: K = 7,55 %, Δυ = 6,25 %.
Результаты вычислительных экспериментов показали сильную корреляционную связь между К и Δυ (вычисленное значение коэффициента ранговой корреляции Спирмена равно 1).
Заключение
Проведенные исследования, подкрепленные конкретным примером, показали, что предложенный критерий адекватно определяет возможности улучшения теплового режима путем рационального размещения электронных элементов, исключает возможность неверных оценок и его можно успешно использовать для принятия решений при проектировании.
Библиографическая ссылка
Меркухин Е.Н. АПРИОРНЫЙ КРИТЕРИЙ ОЦЕНКИ ЭФФЕКТИВНОСТИ ОПТИМИЗАЦИИ ТЕПЛОВОГО РЕЖИМА ПУТЕМ РАЦИОНАЛЬНОГО РАЗМЕЩЕНИЯ ЭЛЕКТРОННЫХ ЭЛЕМЕНТОВ // Современные наукоемкие технологии. 2018. № 10. С. 77-81;URL: https://top-technologies.ru/ru/article/view?id=37198 (дата обращения: 03.03.2026).



