Проблема высокоточных вычислений стоит во многих областях вычислительной математики, математической физики, экономики, биохимии. Для решения таких задач, как прямое и обратное преобразования Лапласа [1], оптимальное управление [2], моделирование процессов метаболизма и конфигурации макромолекул [3], волновое рассеяние [4], требуется точность 256–2048 бит. Другой важной областью применения длинной арифметики являются задачи криптографии, в которых операция умножения длинных целых чисел является основной. При этом повышение скорости является основной целью при построении криптосистем, где длина чисел может достигать нескольких тысяч бит [5]. На сегодняшний день основным способом работы с длинными двоичными числами являются программные библиотеки позиционной длинной арифметики, главным недостатком которых является резкое снижение быстродействия вследствие возникающих единиц переноса между двоичными разрядами длинного позиционного числа. Однако даже самые быстрые способы умножения дают значительное снижение быстродействия на очень длинных числах [6]. Альтернативой длинной позиционной арифметики является модулярная арифметика (системы счисления в остаточных классах, СОК).
СОК – это непозиционная система счисления, которая позволяет заменить последовательные методы выполнения арифметических операций над «длинными» целыми числами в позиционных системах счисления на параллельные методы выполнения арифметических операций над наборами «коротких» целых чисел [7]. Главным преимуществом СОК является высокое быстродействие таких операций, как сложение и умножение (так называемые модульные операции), поскольку нет необходимости фиксировать и распространять единицы переноса между разрядами; существенным недостатком – сложность выполнения немодульных операций, таких как операции масштабирования, сравнения и определения переполнения диапазона представления чисел. Учитывая особенности организации вычислений в СОК, их применение наиболее эффективно для решения задач, алгоритмизация которых реализована с существенным преобладанием модульных операций, особенно операций умножения.
Цель работы: повышение скорости выполнения операции умножения длинных чисел с плавающей точкой. Для повышения скорости вычислений предлагается использовать гибридное модулярное интервально-логарифмическое представление длинных чисел с плавающей точкой, в котором мантисса представлена в системе остаточных классов, а также содержащее в качестве метаданных интервально-логарифмическую характеристику, необходимую для быстрого выполнения операций сравнения и масштабирования.
Гибридный модулярный интервально-логарифмический формат данных
В интервальной арифметике вместо чисел, дискретных точек на числовой оси, используется пара чисел, представляющих собой границы закрытых интервалов, или отрезков числовой оси, что позволяет выполнять расчеты с учетом погрешностей в исходных данных и погрешностей, возникающих в процессе вычислений [8, 9]. При этом все вычисления выполняются таким образом, что результирующий интервал гарантированно содержит точный результат вычислений. В связи с этим интервальная арифметика позволяет повысить достоверность вычислений за счет учета в явном виде влияния ошибок округления [8]. Ширина интервала результата при выполнении арифметических операций в интервальной арифметике является не только критерием точности, но и критерием достоверности, поэтому уменьшение ширины интервала является одной из важных задач. В качестве одного из способов повышения точности интервальной арифметики могут быть применены логарифмические системы счисления (ЛСС) для представления границ интервала [10].
Число в интервально-логарифмическом формате представлено следующим образом:
в качестве одного из способов повышения точности интервала,
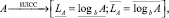
где logb – логарифм числа по основанию b, вычисленный с округлением к минус и плюс бесконечности соответственно, A – модуль числа, представленный в позиционной системе счисления.
Результат умножения двух чисел, представленных в интервально-логарифмическом формате, определяется следующим образом:
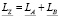 ;
; 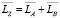 .
.
Система остаточных классов является непозиционной системой счисления, в которой значения позиционного числа A представлены набором n остатков 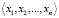 от деления числа A на каждый из n модулей
от деления числа A на каждый из n модулей 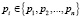 [7]
[7] 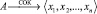 , где xi вычисляется следующим образом:
, где xi вычисляется следующим образом:
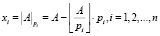 ,
,
где 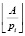 – целая часть частного
– целая часть частного 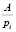 ,
, 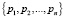 – набор оснований или базис СОК.
– набор оснований или базис СОК.
Произведение 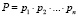 определяет диапазон представления чисел
определяет диапазон представления чисел 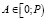 в СОК, причем, если все числа
в СОК, причем, если все числа 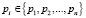 являются попарно взаимно простыми, то между любым положительным целым числом A из диапазона [0; P) и числом, представленным в СОК, имеется взаимно однозначное соответствие.
являются попарно взаимно простыми, то между любым положительным целым числом A из диапазона [0; P) и числом, представленным в СОК, имеется взаимно однозначное соответствие.
Результат умножения двух чисел 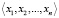 и
и 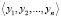 , представленных в СОК, определяется следующим образом:
, представленных в СОК, определяется следующим образом:
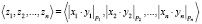 .
.
В данной работе предлагается объединить преимущества обоих рассмотренных форматов представления, модулярного и интервально-логарифмического, в новый гибридный модулярный интервально-логарифмический (МИЛ) формат:
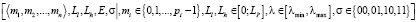 ,
,
где σ – знак числа, 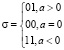 ,
, 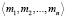 – мантисса числа, представленная в СОК, λ – масштаб (порядок) числа, Ll, Lh – интервально-логарифмическая характеристика (ИЛХ) мантиссы числа,
– мантисса числа, представленная в СОК, λ – масштаб (порядок) числа, Ll, Lh – интервально-логарифмическая характеристика (ИЛХ) мантиссы числа, 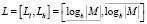 .
.
Метод выполнения операции умножения в модулярном интервально-логарифмическом формате
Пусть заданы два числа в МИЛ-формате
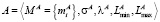
и
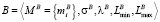 .
.
Тогда результат
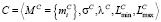
будет вычислен следующим образом:
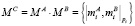 ,
,
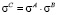 ,
, 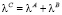 .
.
Поскольку мантиссы чисел, представленных в МИЛ-формате, ограничены диапазоном [0; P – 1), то при выполнении умножения двух мантисс результат может выйти за пределы диапазона представления 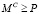 . Для того, чтобы мантисса результата была представима в МИЛ-формате, необходимо выполнить операцию масштабирования
. Для того, чтобы мантисса результата была представима в МИЛ-формате, необходимо выполнить операцию масштабирования 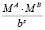 , где
, где 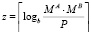 .
.
Будем выполнять масштабирование обоих операндов до выполнения операции умножения таким образом, чтобы масштабированные сомножители не превышали величину 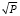 , то есть
, то есть
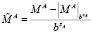 ,
, 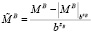 ,
,
где zA и zB – коэффициенты, определяемые соотношениями значений модулей мантисс.
Таким образом, все необходимые вычисления (проверка переполнения, масштабирование) проводятся до непосредственного умножения мантисс.
На основании описанных выше выкладок сформулируем алгоритм умножения двух чисел, представленных в МИЛ-формате.
Шаг 1. Проверка операндов на ноль. Если хотя бы один из операндов равен нулю, то результат равен нулю: σC = 0, λC = 0, 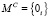 ,
, 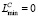 ,
, 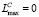 , иначе перейти к следующему шагу.
, иначе перейти к следующему шагу.
Шаг 2. Проверка потери значащих разрядов: если 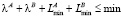 , где
, где 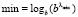 , то есть результат выполнения операции умножения двух чисел меньше, чем минимально представимое по модулю число, то результат равен нулю: σC = 0, λC = 0,
, то есть результат выполнения операции умножения двух чисел меньше, чем минимально представимое по модулю число, то результат равен нулю: σC = 0, λC = 0, 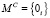 ,
, 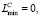
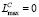 , иначе перейти к следующему шагу.
, иначе перейти к следующему шагу.
Шаг 3. Знак результата: 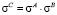 .
.
Шаг 4. Проверка переполнения: если 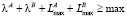 , где
, где 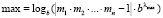 , то есть результат выполнения операции умножения двух чисел выйдет за границы представления чисел в формате IML, то присвоить результату значение «бесконечность»:
, то есть результат выполнения операции умножения двух чисел выйдет за границы представления чисел в формате IML, то присвоить результату значение «бесконечность»: 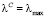 ,
, 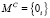 ,
, 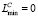 ,
, 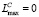 , иначе перейти к следующему шагу.
, иначе перейти к следующему шагу.
Шаг 5. Проверка переполнения результата умножения модулярных мантисс. В случае, если результат умножения двух модулярных чисел выходит за границы представления, необходимо предварительно уменьшить один их сомножителей или оба сразу путем масштабирования степенью b. Если 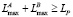 , где
, где 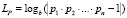 , то вычислить значения масштабирующих коэффициентов:
, то вычислить значения масштабирующих коэффициентов: 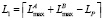 ,
, 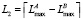 , если
, если 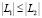 и
и 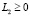 , то
, то 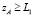 ,
, 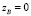 ; если
; если 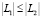 и L < 0, то
и L < 0, то 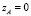 ,
, 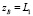 ; если
; если 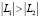 и
и 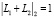 , то
, то 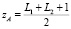 ,
, 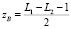 ; если
; если 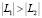 и
и 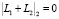 , то
, то 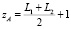 ,
, 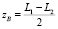 . Если
. Если 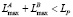 , то перейти к шагу 7.
, то перейти к шагу 7.
Шаг 6. Вычислить значения скорректированных мантисс 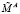 и
и 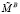 операндов и скорректировать значение верхней и нижней границы интервальной логарифмической характеристики результата:
операндов и скорректировать значение верхней и нижней границы интервальной логарифмической характеристики результата:
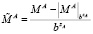 ,
, 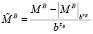 .
.
Скорректировать значения верхней и нижней границ ИЛХ чисел A и B:
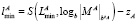 ;
;
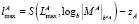 ;
;
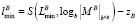 ;
;
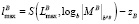 ,
,
где 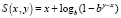 , если y < x,
, если y < x, 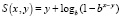 , если y > x.
, если y > x.
Шаг 7. Выполнить модулярное умножение мантисс: 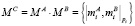 или
или 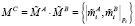 , если мантиссы были скорректированы на шаге 6. Масштаб (порядок) результата:
, если мантиссы были скорректированы на шаге 6. Масштаб (порядок) результата: 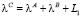 . ИЛХ результата:
. ИЛХ результата: 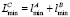 ,
, 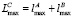 .
.
Оценка быстродействия
Время выполнения предложенного метода (без учета исключений) равно
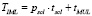 ,
,
где pscl – доля случаев, при которых требуется операция масштабирования – вероятность того, что произведение двух мантисс выйдет за пределы диапазона представления модулярных мантисс, tscl – время выполнения операции масштабирования, tMUL – время модулярного умножения.
Предположим, что числа из диапазона [0; P) могут появиться с равной вероятностью. Вероятность того, что произведение двух мантисс выйдет за пределы диапазона представления модулярных мантисс, то есть 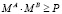 , равна
, равна
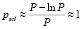 .
.
Время выполнения операции масштабирования равно [11]:
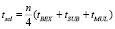 ,
,
где tBEX – время выполнения операции расширения базиса, tSUB – время модулярного вычитания, tMUL – время модулярного умножения.
Время расширения базиса при использовании самого быстрого алгоритма равно [11] 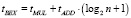 .
.
Таким образом, общее время выполнения разработанного метода не превышает 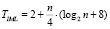 тактов.
тактов.
Сравним разработанный метод и метод умножения длинных чисел с плавающей точкой [12], время выполнения которого составляет 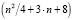 тактов, а также с одним из асимптотически быстрых методов умножения, используемых для организации некоторых целочисленных двоичных умножителей (алгоритм Карацубы) [6]. Зависимость времени выполнения метода от разрядности операндов представлена на рисунке.
тактов, а также с одним из асимптотически быстрых методов умножения, используемых для организации некоторых целочисленных двоичных умножителей (алгоритм Карацубы) [6]. Зависимость времени выполнения метода от разрядности операндов представлена на рисунке.
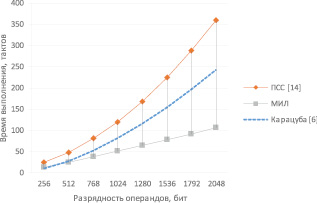
Сравнение быстродействия разработанного метода и методов, основанных на позиционном представлении длинных чисел
Разработанный метод в среднем приблизительно в 3,4 раза быстрее метода, основанного на позиционной длинной арифметике, и в 2,3 раза быстрее одного из асимптотически наиболее быстрых, но в явном виде практически не используемого алгоритма (алгоритм Карацубы) для разрядности мантисс 2048 бит.
Заключение
Разработан метод выполнения операции умножения с использованием модулярного интервально-логарифмического представления чисел с плавающей точкой. Отличительной особенностью представленного метода является использование интервальных логарифмических характеристик для быстрого выполнения немодульных операций сравнения и масштабирования. Разработанный метод в среднем приблизительно в 3,4 раза быстрее метода, основанного на позиционной длинной арифметике, и в 2,3 раза быстрее одного из асимптотически наиболее быстрых, но в явном виде практически не используемого алгоритма (алгоритм Карацубы) для разрядности мантисс 2048 бит.
Сложность разработанного метода выполнения умножения 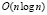 , что быстрее, чем асимптотически быстрые алгоритмы умножения чисел в позиционной системе счисления: Шёнхаге – Штрассена, имеющего сложность
, что быстрее, чем асимптотически быстрые алгоритмы умножения чисел в позиционной системе счисления: Шёнхаге – Штрассена, имеющего сложность 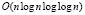 , и Фюрера со сложностью
, и Фюрера со сложностью 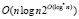 .
.
Представленный метод защищен патентом РФ [13]. В качестве дальнейших направлений исследований предлагается разработка быстрых методов выполнения операций расширения базиса и масштабирования, что позволит уменьшить время выполнения операции умножения чисел в МИЛ-формате.
Исследование выполнено при финансовой поддержке РФФИ в рамках научного проекта № 18-37-00278 мол_а.
Библиографическая ссылка
Коржавина А.С., Князьков В.С. МЕТОД УСКОРЕННОГО УМНОЖЕНИЯ В СИСТЕМЕ ОСТАТОЧНЫХ КЛАССОВ С ИСПОЛЬЗОВАНИЕМ ЛОГАРИФМИЧЕСКИХ ИНТЕРВАЛЬНЫХ ХАРАКТЕРИСТИК // Современные наукоемкие технологии. 2018. № 10. С. 60-64;URL: https://top-technologies.ru/ru/article/view?id=37195 (дата обращения: 22.02.2026).
DOI: https://doi.org/10.17513/snt.37195



