Так как многие объекты управления размещаются в труднодоступных местах за полярным кругом, то организация с центром управления осуществляется с использованием низкоорбитальных систем спутниковой связи (НССС). Так как число группировок НССС постоянно будет возрастать, то может получиться ситуация, когда в зоне видимости приемной станции спутниковой связи, находящейся на необслуживаемом объекте управления, появится спутник-нарушитель. С целью противодействия навязыванию ранее перехваченной команды управления, в работе [1] предлагается использовать систему аутентификации космического аппарата (КА). Очевидно, что уровень информационной скрытности НССС будет определяться протоколом аутентификации, которые в своем алгоритме используют большие простые числа. Для снижения временных затрат, необходимых на проверку статуса космического аппарата, в работе [2] предлагается использовать модулярные коды (МК). Но прежде чем производить вычисления в МК, необходимо осуществить прямое преобразование из позиционной системы счисления (ПСС) в МК. Поэтому разработка алгоритмов прямого преобразования ПСС-МК, требующих минимальных временных затрат, является актуальной задачей.
Цель исследования: с целью повышения информационной скрытности НССС в системе определения статуса КА используют протоколы аутентификации, которые базируются на доказательстве с нулевым разглашением знаний. Для обеспечения высокой криптостойкости в таких протоколах используются большие простые числа, что приводит к увеличению временных и схемных затрат. Использование МК в протоколах аутентификации КА позволяет повысить скорость вычислений, так как операции сложения, вычитания и умножения выполняются параллельно и с малоразрядными операндами по основаниям р1, р2, ..., рk. Однако для перехода от позиционного кода к модулярному коду необходимо выполнить обязательную операцию – прямое преобразование ПСС-МК, что приводит к увеличению временных затрат. Целью исследований является снижение временных затрат на выполнение прямого преобразования ПСС-МК для систем аутентификации КА, функционирующей в МК.
Материалы и методы исследования
Интеграция свойств модулярных кодов в протоколы аутентификации, использующие доказательство с нулевым разглашением знаний, позволила повысить скорость выполнения определения статуса спутника. Основу МК составляют остатки, которые получаются путем делении целого числа Х на основания системы р1, р2, ..., рk . Тогда модулярный код имеет вид
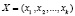 , (1)
, (1)
где 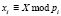 ;
; 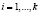 ; НОД(рi, pj) = 1;
; НОД(рi, pj) = 1; 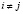 .
.
Как показано в работах [3–5], непозиционный МК позволяет повысить скорость выполнения модульных операций сложения, вычитания и умножения, так как справедливо
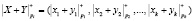 , (2)
, (2)
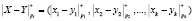 , (3)
, (3)
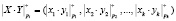 , (4)
, (4)
где 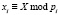 ;
; 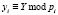 ;
; 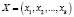 и
и 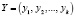 – модулярный код.
– модулярный код.
При этом набор оснований в МК выбирают так, чтобы операнды X, Y, а также результаты вычислений не выходили за пределы рабочего диапазона, определяемого как
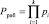 . (5)
. (5)
Рассмотрим протокол аутентификации КА, реализованный МК, который использует секретный ключ 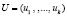 , сеансовый ключ
, сеансовый ключ 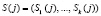 , параметр
, параметр 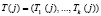 , применяемый для проверки повторного использования сеансового ключа, где
, применяемый для проверки повторного использования сеансового ключа, где 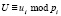 ;
; 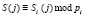 ;
; 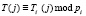 ; i = 1, 2,…, k. Протокол состоит в следующем.
; i = 1, 2,…, k. Протокол состоит в следующем.
1. На борту КА происходит вычисление истинного статуса КА, представленного в МК
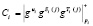 , (6)
, (6)
где g – порождающий мультипликативную группу по модулю рi; i = 1, 2,…, k.
2. Затем на борту КА производится «зашумление» параметров протокола
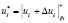 ;
; 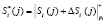 ;
; 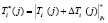 . (7)
. (7)
где 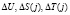 – случайные значения;
– случайные значения; 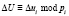 ;
; 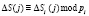 ;
; 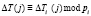 ; i = 1, 2,…, k.
; i = 1, 2,…, k.
3. На борту КА определяется зашумленный статус космического аппарата в МК
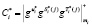 . (8)
. (8)
4. При аутентификации КА запросчик передает случайное число d = (d1,…, dk).
5. Спутник, получив «вопрос» d = (d1,…, dk), вычисляет ответы на него
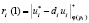 ;
; 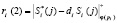 ;
; 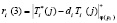 . (9)
. (9)
6. Спутник, передает запросчику истинный и зашумленный статусы, а также ответы на поставленный «вопрос» d.
7. Запросчик производит аутентификацию КА согласно
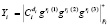 . (10)
. (10)
Если полученный результат совпадает с зашумленным статусом, то запросчик считает спутник «своим».
Очевидно, что для осуществлений вычислений в МК необходимо выполнить прямое преобразование из ПСС в модулярный код. Известно, что данная операция считается немодульной и ее временные затраты определяются соответствующими алгоритмом [3–5]. Получить остаток числа Х по модулю pi, где i = 1, 2,…, k, можно путем простого деления, т.е.
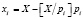 , (11)
, (11)
где 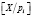 – наименьшее целое от деления целого числа Х на основание pi.
– наименьшее целое от деления целого числа Х на основание pi.
Так как модулярный код, который задан взаимно простыми основаниями 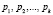 , представляет собой алгебраическую систему кольца, то в данной системе отсутствует операция деления. Это привело к необходимости разработки алгоритмов вычисления остатка через последовательность модульных операций.
, представляет собой алгебраическую систему кольца, то в данной системе отсутствует операция деления. Это привело к необходимости разработки алгоритмов вычисления остатка через последовательность модульных операций.
Так, в работе [5] представлен алгоритм вычисления остатка на основании метода уменьшения разрядности. Данный алгоритм базируется на свойствах сравнимости. Представим исходное число Х в двоичном коде, где разряды 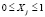 . Тогда имеем
. Тогда имеем
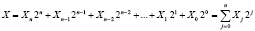 . (12)
. (12)
Затем вычисляются остатки по модулю pi каждого веса двоичного кода числа Х
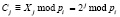 . (13)
. (13)
Полученные значения Cj подставляются вместо степеней двойки в выражение (12). Используя свойство сравнимости, получаем сумму
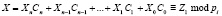 . (14)
. (14)
Очевидно, что полученное значение Z1 будет иметь меньшую разрядность, чем исходное число Х. Затем алгоритм выполняется с числом Z1. В результате будет получено число Z2 меньшей размерности, чем Z1. Алгоритм будет повторяться до тех пор, пока не будет получена сумма, удовлетворяющая условию ZL < pi. Полученный результат и будет остатком числа X по модулю pi
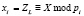 . (15)
. (15)
Основным достоинством данного алгоритма, использующего понижение разрядности, является использование при определении остатка простого позиционного сумматора. Несмотря на простоту схемной реализации, данный алгоритм имеет недостатки:
– значительные временные затраты при большой разрядности операнда Х;
– необходимо осуществлять проверку окончания процесса после каждой итерации.
Наряду с алгоритмами с понижением разрядности в вычислительных устройствах, функционирующих в модулярном коде, применяются алгоритмы, использующие методы непосредственного суммирования [3, 4]. В основу данных алгоритмов положено использование констант, которые представляют собой остатки по модулю pi всех степеней оснований 2j и коэффициентов при соответствующих степенях оснований Хj, то есть
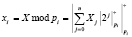 . (16)
. (16)
Тогда последовательный алгоритм преобразования ПСС-МК имеет вид
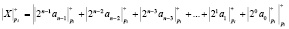 . (17)
. (17)
Структурная модель, реализующая алгоритм (17), показана на рис. 1.

Рис. 1. Структурная модель выполнения последовательного алгоритма ПСС-МК
Операнд Х, представленный в ПСС, записывается в регистр сдвига на bj разрядов, где 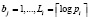 . Блок из bj разрядов поступает на первую просмотровую таблицу (LUT1), с выхода которой снимается значение остатка по модулю pi степеней оснований 2j при соответствующих значениях коэффициентов Xj. Вторая просмотровая таблица (LUT2) выполняет последовательное вычисление остатка по модулю рi. Промежуточный результат записывается в регистр (Register). По окончанию алгоритма вычисленное значение остатка числа Х по модулю рi подается в аккумулятор (Accumulator), а затем на выход. При реализации алгоритма (17) время вычисления остатка числа по модулю составит
. Блок из bj разрядов поступает на первую просмотровую таблицу (LUT1), с выхода которой снимается значение остатка по модулю pi степеней оснований 2j при соответствующих значениях коэффициентов Xj. Вторая просмотровая таблица (LUT2) выполняет последовательное вычисление остатка по модулю рi. Промежуточный результат записывается в регистр (Register). По окончанию алгоритма вычисленное значение остатка числа Х по модулю рi подается в аккумулятор (Accumulator), а затем на выход. При реализации алгоритма (17) время вычисления остатка числа по модулю составит
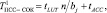 (18)
(18)
где tLUT – время выборки из LUT-таблицы; tACC – время срабатывания аккумулятора.
Основным достоинством последовательного алгоритма вычисления остатка числа Х по модулю являются низкие схемные затраты на реализацию прямого преобразования ПСС-МК. Однако данный алгоритм имеет недостаток – значительные временные затраты, которые увеличиваются при увеличении разрядности операнда Х.
С целью устранения данного недостатка был модифицирован алгоритм параллельного определения остатка на основе распределенной арифметики. Для этого двоичный код числа разбивается на блоки, состоящие из В разрядов
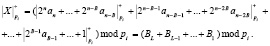 (19)
(19)
Затем определяются остатки по модулю каждого из блоков B1,…, BL согласно
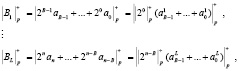 (20)
(20)
где 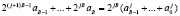 ;
; 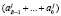 – двоичный код Вj блока.
– двоичный код Вj блока.
На рис. 2 представлена структурная модель, реализующая модифицированный алгоритм параллельного определения остатка на основе распределенной арифметики (20). Временные затраты при использовании модификации алгоритма (20) составят
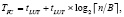 (21)
(21)
где В – размер блока; n – размер входного операнда; tLUT – время выборки из LUT-таблицы.
Результаты исследования и их обсуждение
Пусть необходимо вычислить остаток числа Х = 32015 по модулю р = 17. Представим в двоичном коде число Х = 32015 = 0111 1101 0000 11112. Воспользуемся последовательным алгоритмом (12) при длине блока bj = 1. Тогда получаем
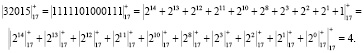
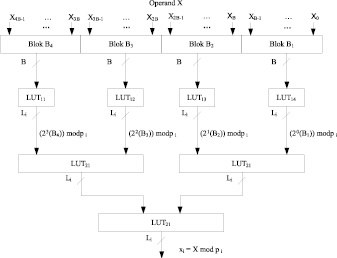
Рис. 2. Структурная модель, реализующая алгоритм (20) ПСС-МК
Согласно (18) время вычисления остатка при условии tLUT = tACC составит
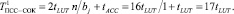
Сократим время вычисления остатка, увеличив размерности блока bj = 2. В этом случае число Х = 3201510 = 01 11 11 01 00 00 11 112. Тогда
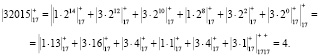
В этом случае время вычисления остатка составит
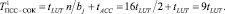
Рассмотрим модифицированный алгоритм параллельного определения остатка на основе распределенной арифметики (15). Двоичный код числа Х = 32015 разобьем на блоки по В = 4 бит. Тогда получаем Х = 32015 = 0111 1101 0000 1111. В результате получили 4 числа В4 = 7, В3 = 13, В2 = 0, В1 = 15. Тогда остаток по модулю 17 будет равен
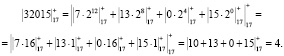
Временные затраты при использовании модификации алгоритма (20) составят
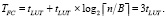
Проведенные исследования показали, что использование модификации алгоритма параллельного определения остатка на основе распределенной арифметики позволяет обеспечить максимальную скорость вычисления остатка числа. Применение данного алгоритма при обработке 16-разрядных операндов позволило сократить временные затраты в 5,67 раз по сравнению с последовательным алгоритмом (17) при bj = 1 и в 3 раза – при использовании длины блока, равной bj = 2.
Заключение
Для снижения временных затрат, необходимых на проверку статуса космического аппарата, используются модулярные коды. Но прежде чем будет выполняться протокол аутентификации в МК, необходимо осуществить прямое преобразование из позиционной системы счисления в МК. Поэтому разработка алгоритмов прямого преобразования ПСС-МК, требующих минимальных временных затрат, является актуальной задачей. В статье представлена модификация алгоритма параллельного определения остатка на основе распределенной арифметики. Проведенные исследования показали, что применение данного алгоритма при обработке 16-разрядных операндов позволило сократить временные затраты в 5,67 раз по сравнению с последовательным алгоритмом при bj = 1 и в 3 раза – при использовании длины блока равной bj = 2. Полученные результаты свидетельствуют о целесообразности разработанного алгоритма прямого преобразования в системах аутентификации космического аппарата, функционирующего в модулярных кодах.
Исследование выполнено при финансовой поддержке РФФИ в рамках научного проекта № 18-07-01020.
Библиографическая ссылка
Калмыков М.И., Степанова Е.П., Ефременков И.Д., Ефимович А.В., Калмыков И.А., Тынчеров К.Т. РЕАЛИЗАЦИЯ АЛГОРИТМОВ ВЫПОЛНЕНИЯ ПРЯМОГО ПРЕОБРАЗОВАНИЯ ИЗ ПОЗИЦИОННОГО КОДА В МОДУЛЯРНЫЙ КОД ДЛЯ СИСТЕМЫ АУТЕНТИФИКАЦИИ КОСМИЧЕСКОГО АППАРАТА // Современные наукоемкие технологии. 2018. № 10. С. 44-49;URL: https://top-technologies.ru/ru/article/view?id=37192 (дата обращения: 03.03.2026).



