Катодная защита является одним из распространенных средств борьбы с коррозией подземных трубопроводов. Эффективность катодной защиты зависит от правильного выбора ее эксплуатационных параметров, при этом одной из важнейших является задача расчета характеристик электрического поля в системе «анод – грунт – защищаемое сооружение». Выбор проектных параметров и режимов эксплуатации катодной защиты осуществляется на основе результатов расчетов, для интерпретации которых может быть применена постобработка и визуализация [1, 2].
Цель исследования: разработка подхода к компьютерному моделированию и визуализации электрических полей катодной защиты от коррозии подземных трубопроводов.
Материалы и методы исследования
Рассматривается электрическое поле, создаваемое протяженным цилиндрическим катодом (трубой) и заглубленным вертикальным анодом в области Ω = {p = p (x,y,z): 0 ≤ x ≤ L; z ≤ Ht}. Центральная ось трубы совпадает с осью Ox, на интервале 0 ≤ x ≤ L. Плоскость z = Ht соответствует поверхности земли. Заглубленный анод размещается перпендикулярно поверхности земли, его центр находится в точке p0. Схема катодной защиты приведена на рис. 1.
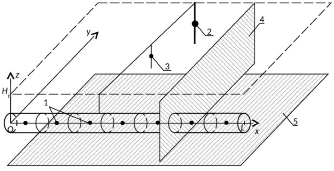
Рис. 1. Условная схема катодной защиты; фиктивные источники, соответствующие: 1 – фрагментам трубы, 2 – заглубленному аноду, 3 – защитному заземлителю; 4, 5 – плоскости визуализации
В заданных условиях распределение электрического потенциала u = u(p) в Ω будет удовлетворять уравнению Пуассона [3, 4]
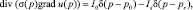 (1)
(1)
где δ (p) – дельта-функция, σ (p) – удельная электропроводность среды, I0, – интенсивность точечного анода, расположенного в точке p0, Is – интенсивность точечного стока, расположенного в точке ps (утечка через заземлители).
На границе Sgt (поверхность трубы) поставим граничные условия третьего рода
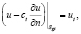 (2)
(2)
где ut – потенциал металла трубы, ct = ct (x) – удельное электрическое сопротивление изоляции трубы (Ом×м2). Считаем, что потенциал металла зависит только от координаты x, т.е. ut = ut (x). На участках Sis (изоляторы: левая и правая границы участка, поверхность земли) поставим граничное условие второго рода
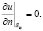 (3)
(3)
Для плотности тока в металле трубы, при отсутствии потерь через боковую поверхность, выполняется закон Ома
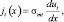 (4)
(4)
где σmt – удельная электропроводность металла трубы.
В точке подключения трубы к катодной станции поставим условие
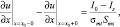 (5)
(5)
где Sms – площадь сечения металла трубы.
Для решения рассматриваемой задачи перейдем к дискретной модели, применяя метод фиктивных источников [5, 6]. Рассматриваемый участок трубы 0 ≤ x ≤ L условно разбиваем на M равных фрагментов. Каждый фрагмент отождествим с точечным источником (стоком), расположенным в геометрическом центре фрагмента (рис. 1). Все электрические параметры каждого точечного источника (стока) принимаем равными среднему для соответствующего фрагмента трубы значению, i = 1..M:
Itg,i – ток через боковую поверхность трубы;
Utm,i – потенциал металла трубы;
Itx,i – продольный ток в металле трубы между соседними фрагментами трубы;
Utg,i – потенциал на границе «грунт – труба».
Для полученной системы точечных источников и стоков выполняется 1 закон Кирхгофа:
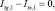
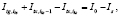
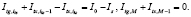 (6)
(6)
где iks – номер фиктивного источника (стока), в котором осуществлен контакт с электрической цепью катодной станции.
Электрический ток в металлическом сечении трубы подчиняется закону Ома, дискретный аналог которого имеет вид
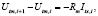 (7)
(7)
где Rm = ρt (lt/Sms) – электрическое сопротивление между соседними фрагментами трубы, ρt – удельное электрическое сопротивление металла трубы, lt – длина фрагмента трубы.
Потенциал на границе «грунт – труба» можно выразить на основе принципа электростатической аналогии [4]
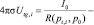
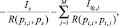 (8)
(8)
где pt,i – центр фиктивного источника с номером i = 1..M, R(p,q) – расстояние между точками p, q.
Параметр Utg,i представляет собой средний для фрагмента трубы потенциал на границе «грунт – труба». Длина фрагмента может быть выбрана достаточно большой, и оказаться сравнимой с другими геометрическими параметрами (например, расстоянием от трубы до анода). В связи с этим, в соотношении (8) будем дополнительно учитывать особенности вычисления электрического потенциала, создаваемого цилиндрическим электродом [7, 8]. Также при расчетах в (8) применим принцип зеркальных отражений [9] и учтем дополнительные источники и стоки.
Дискретные аналоги выражения (2) запишем в виде
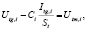 (9)
(9)
где Ci – сопротивления изоляции, St – площадь внешней поверхности фрагмента трубы.
Построенная система 4M–1 линейных уравнений (6)–(9), c 4M–1 неизвестными имеет хорошо обусловленную матрицу и для ее решения можно применить метод Гаусса с выбором главного элемента. Для получения апостериорной оценки погрешности дискретизации, имеющей место при переходе от непрерывной модели (1)–(5) к дискретной (6)–(9), можно применить правило Рунге двойного пересчета [3]. Вводя общее обозначение 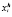 для компонент решения системы (6)–(9), полученного при длине фрагмента h, главный член погрешности можно выразить [4]
для компонент решения системы (6)–(9), полученного при длине фрагмента h, главный член погрешности можно выразить [4]
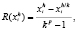 (10)
(10)
где k > 0, p – порядок точности метода, который можно вычислить в соответствии с алгоритмом Эйткена [4]
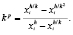 (11)
(11)
Решая систему (6)–(9), найдем интенсивности Itg,i. Тогда, распределение в области Ω потенциала, создаваемого точечными источниками (стоками) с интенсивностями I0, Is, Itg,i, расположенными в точках p0, ps, pt,i соответственно, описывается уравнением Пуассона [3]
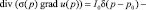
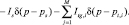 (12)
(12)
Уравнение (12) дополним граничными условиями второго рода на участках Sis
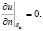 (13)
(13)
Применяя принцип электростатической аналогии [9], можем записать выражение для электрического потенциала в произвольной точке q∈ Ω
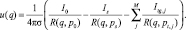 (14)
(14)
Так же, как и для соотношения (8), при расчетах в (14) применим принцип зеркальных отражений и учтем дополнительные источники и стоки [4].
Векторная величина плотности тока может быть выражена, как [3]
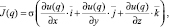 (15)
(15)
где 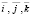 – c орты координатных осей.
– c орты координатных осей.
В области Ω введем прямоугольную трехмерную сетку с постоянным шагом h; в узловых точках qi,j,k вычислим электрический потенциал ui,j,k = u (qi,j,k).
В (13) заменяя частные производные конечными разностями [3], например, для переменной x
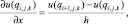 (16)
(16)
можем найти компоненты векторного поля плотности тока (15) в узловых точках.
Результаты исследования и их обсуждение
Предложенный подход позволяет получить распределение электрического потенциала в виде трехмерного скалярного поля, а также компоненты трехмерного векторного поля плотности тока в рассматриваемой области. Однако трехмерные данные представляют сложности для восприятия и визуализации [10], в связи с этим графические построения были осуществлены для двумерных сечений исходной области Ω (рис. 1).
Предлагаемый алгоритм реализован в виде программы на языке С++, с использованием которой проведены расчеты с реальными исходными данными (таблица). Применен алгоритм Эйткена [11]; порядок точности численного метода принят равным 1. Полученная по правилу Рунге общая относительная погрешность численных результатов составила менее 1 %.
Исходные данные задачи
|
Параметр |
Значение |
|
Внешний диаметр трубы, м |
0,557 |
|
Глубина до центра анода, м |
2,5 |
|
Глубина залегания трубы, м |
1,5 |
|
Длина защищаемого участка трубы, м |
11000 |
|
Интенсивность утечки, в % от тока катодной станции |
10 |
|
Координата точки х подключения СКЗ к трубе, м |
5500 |
|
Расстояние от анода до трубы, м |
200 |
|
Расстояние от утечки до трубы, м |
20 |
|
Ток катодной станции I0, А |
4 |
|
Толщина стенки трубы, мм |
8 |
|
Удельное сопротивление грунта, Ом·м |
200 |
|
Удельное сопротивление стали, Ом·м |
2,45e–7 |
|
Число принятых фрагментов по трубе |
1000 |
Результаты расчетов представлены в формате текстовых файлов с разделителями «точка с запятой». Каждый такой файл содержит значения электрического потенциала в некотором заданном двумерном сечении трехмерной области Ω (рис. 1).
Для визуализации результатов расчетов была разработана программа в математическом пакете Octave, осуществляющая импорт данных из файлов, вычисление компонент векторного поля, подготовку и графический вывод результатов [12]. Далее приведены некоторые результаты вычислительных экспериментов.
Эксперимент 1. Расчет электрического потенциала и векторного поля плотности тока в области Ω1 = {x = 3000; –4 ≤ y ≤ 4; –3,5 ≤ z ≤ 1,5}. Результаты приведены на рис. 2, 3.
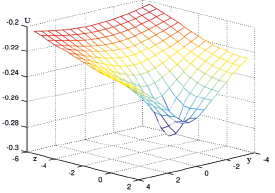
Рис. 2. Распределение потенциала (Эксперимент 1)
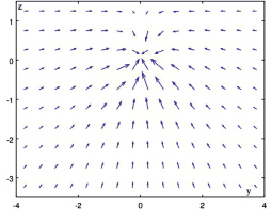
Рис. 3. Векторное поле плотности тока (Эксперимент 1)
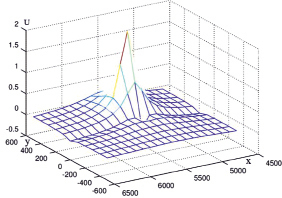
Рис. 4. Распределение потенциала (Эксперимент 2)
Эксперимент 2. Расчет электрического потенциала и векторного поля плотности тока в области Ω2 = {4500 ≤ x ≤ 6500; –600 ≤ y ≤ 600; z = –5}. Пример результата визуализации приведен на рис. 4.
Полученные результаты позволяют наблюдать следующее:
– На защищаемом участке наибольший электрический потенциал имеет место в точках, близких к заглубленному аноду, по мере удаления от которого потенциал снижается;
– Наименьшие значения потенциала наблюдаются вблизи трубопровода, который выступает в роли катода;
– На рис. 3, иллюстрирующем векторное поле плотности тока, наблюдается течение тока от участков с более высоким потенциалом к участкам с низким потенциалом.
Заключение
Полученные результаты, общая картина и характер токораспределения согласуются с результатами натурных измерений, предлагаемые методы расчета и визуализации параметров электрического поля могут быть применены при проектировании и выборе режимов эксплуатации систем катодной защиты подземных трубопроводов.
Данная работа была выполнена в рамках государственного задания № 5753.
Библиографическая ссылка
Хисаметдинов Ф.З. КОМПЬЮТЕРНОЕ МОДЕЛИРОВАНИЕ И ВИЗУАЛИЗАЦИЯ ПАРАМЕТРОВ ЭЛЕКТРИЧЕСКОГО ПОЛЯ КАТОДНОЙ ЗАЩИТЫ ПОДЗЕМНОГО ТРУБОПРОВОДА // Современные наукоемкие технологии. 2018. № 9. С. 126-130;URL: https://top-technologies.ru/ru/article/view?id=37172 (дата обращения: 12.02.2026).
DOI: https://doi.org/10.17513/snt.37172



