Транспортная сеть городов должна обеспечивать комфортное передвижение как для автомобильного транспорта, так и для пешеходов. Игнорировать пешеходное движение не представляется возможным при составлении адекватных математических моделей распределения транспортных потоков по сети. Увеличение интенсивности, изменение скоростных режимов транспортных потоков предъявляют все более жесткие требования к средствам управления движением, к уровню их эффективности и безопасности для всех конфликтных сторон.
Пешеходное движение в крупных городах оказывает значительное влияние на величину транспортных задержек, в частности на перекрестках. Причем интенсивность пешеходных потоков неравномерна в течение суток, зависит от дней недели, времени года. Поэтому выбрать оптимальную на все случаи схему организации движения невозможно.
Для выработки надежных, оптимальных в определенных условиях решений необходимо иметь адекватные исходные данные, отражающие реальную ситуацию, и адекватную математическую модель, способную учесть их влияние на критерии эффективности. Кроме того, сами эти критерии являются субъективными и в большой степени зависят от конкретной поставленной задачи.
Изучением формирования пешеходных потоков, их влянием на загрузку сети занимаются как отечественные ученые [1–3], так и зарубежные [4, 5]. Однако разработка метода определения оптимальной организации движения на перекрестке остается актуальной задачей.
Цель исследования: разработка метода определения оптимальной схемы организации пешеходного движения на перекрестке с учетом динамически изменяющегося распределения интенсивностей транспортных потоков.
Материалы и методы исследования
Оптимизировать схему организации движения на отдельном перекрестке достаточно тяжело уже потому, что требуется учитывать интересы всех участников движения. В зависимости от выбора критерия оптимизации, могут быть получены различные результаты решения поставленной задачи. Кроме того, принимать эти решения приходится зачастую в условиях неопределенности по отдельным факторам. В таких ситуациях применимы математические методы теории игр (в данном случае – игр с «природой»). Результат все равно получается в некоторой степени субъективным, зависит от выбора критерия, но позволяет систематизировать данные и способствует повышению качества принимаемых в услових неопределнности решений.
В качестве математической модели распределения движения транспортных потоков по сети взята модель TIMeR_Mod [6], разработанная Н.А. Наумовой В качестве гипотезы о распределении интервалов по времени в каждом из потоков требований в данной модели принята гипотеза о том, что оно подчинено обобщенному закону Эрланга. Это многопараметрический закон, который позволяет описывать транспортные потоки достаточно высокой плотности. Пешеходные потоки приняты распределенными по показательному закону. Показательный закон является частным случаем обобщенного закона Эрланга, поэтому ко всем конфликтующим потокам (как пешеходным, так и транспортным) может быть применен единый подход в аналитических рассуждениях.
TIMeR_Mod – это мезоскопическая модель, основанная на аналитических расчетах всех показателей эффективности, что позволяет применять ее в тех случаях, когда требуется оперативность реагирования на изменяющуюся ситуацию. Еще одним преимуществом данной модели является возможность ее применения в автоматизированнных системах управления движением, включенных в общую интеллектуальную транспортную систему.
Результаты исследования и их обсуждение
Моделирование конфликтной ситуации на перекрестке
Итак, моделью конфликтной ситуации на перекрестке является антагонистическая игра двух игроков, в которой осознанно выбирать свои стратегии может только один из них. Поэтому будем рассматривать данную конфликтную ситуацию как «игру с природой» [7]. Второй игрок, «природа», специально не противодействует первому, а принимает то или иное свое состояние неопределенным образом.
Игрок A – пешеходный поток через конкретный перекресток. Возможные стратегии игрока A:
– A1 – жесткий цикл регулирования с выделением отдельной фазы для пешеходного потока;
– A2 – жесткий цикл регулирования без выделения отдельной фазы для пешеходного потока;
– A3 – использование вызывных устройств для пешеходного движения.
Неопределенность при принятии решений вызвана в данной ситуации состояниями объективной действительности (игрока B) – изменяющимися с течением времени интенсивностями транспортных и пешеходных потоков. Игрок B оказывает противодействие игроку A неосознанно. Стратегии игрока B, «природы», – распределения интенсивностей автомобильных и пешеходных потоков на данном перекрестке.
Важный момент – задание элементов платежной матрицы. Их выбор зависит от выставленных приоритетов, от доминирующего критерия оптимизации. Если ставить во главу угла организацию пешеходного потока через перекресток, то элементами платежной матрицы могут быть величины, обратные значению средней задержки отдельного пешехода на перекрестке. Назовем это интенсивностью обслуживания пешеходов.
Итак, платежная матрица имеет вид
 , (1)
, (1)
Qj, j = 1,...,n – возможные состояния «природы» в рассматриваемый промежуток времени, расчитанные с использованием регрессионных зависимостей (с заданным шагом по времени от текущего момента) интенсивности всех конфликтных потоков, как транспортных, так и пешеходного;
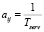 – интенсивность обслуживания пешеходов при справедливости стратегий Ai и Qj;
– интенсивность обслуживания пешеходов при справедливости стратегий Ai и Qj;
Tserv – средняя задержка пешехода при пересечении перекрестка в выбранном направлении при справедливости стратегий Ai и Qj.
Варианты выбора критерия также возможны. Предлагается использовать либо максиминный критерий Вальда, либо критерий минимального риска Сэвиджа.
По критерию Вальда оптимальной считается стратегия, отвечающая условию
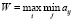 . (2)
. (2)
В этом случае оптимальной будет признана та схема организации движения на перекрестке, которая среди всех возможных, неудачных для пешеходов, ситуаций в распределении транспортных потоков в рассматриваемый промежуток времени гарантирует выбор наилучшей (с максимальной интенсивностью обслуживания пешеходов).
Наибольший элемент j-го столбца 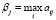 (j = 1,...,n) называют показателем благоприятности состояния Qj.
(j = 1,...,n) называют показателем благоприятности состояния Qj.
Для применения критерия минимального риска Сэвиджа необходимо построить матрицу рисков:
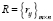 , (3)
, (3)
где 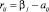 – риск игрока A как упущенная возможность максимального выигрыша (невыигранная часть максимального выигрыша).
– риск игрока A как упущенная возможность максимального выигрыша (невыигранная часть максимального выигрыша).
Оптимальный вариант по критерию Сэвиджа отвечает условию
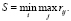 (4)
(4)
Определение элементов платежной матрицы
Рассмотрим вопрос определения возможных состояний «природы» Qj – вариантов распределения интенсивностей транспортных и пешеходных потоков. Исходными данными для решения различных транспортных задач с помощью модели TIMeR_Mod является текущая схема организации движения на улично-дорожной сети и параметры распределения транспортных потоков по полосам, определяемые на основании данных мониторинга. Вся необходимая для расчетов информация содержится в матрицах ASTREETS и BINTERSECTION. В статье [8] авторами разработан метод прогнозирования элементов этих матриц на следующий период времени с примененим фильтра Кальмана, а также метод их автоматизированного расчета. Для определения состояний Qj через интервалы Δt предлагается использовать вышеуказанный метод.
Стратегия A1. Рассмотрим перекресток с жестким режимом регулирования и отдельной фазой для пешеходного потока. Предположим, что прибытие пешехода к перекрестку случайно, не зависит от фаз светофорного цикла. Тогда момент прибытия пешехода можно считать распределенным равномерно относительно фаз светофорного цикла. Если в этот момент движение пешехода разрешено, то затраченое время только Tcrossp, в противном случае пешеход ожидает возможности продожить движение. Согласно законам теории вероятностей, среднее время ожидания отдельным пешеходом возможности продолжить движение в случае, если он прибыл в момент горения запрещающего сигнала, равно
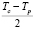 секунд,
секунд,
где Tc – длина цикла регулирования, с.,
Tp – отдельная фаза светофорного цикла, время, в течение которого разрешено движение пешеходов в выбранном направлении, с.
Тогда среднее время, необходимое пешеходу для продолжения движения через перекресток Tserv, равно
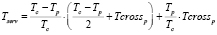 , (5)
, (5)
где Tcrossp – среднее время, необходимое пешеходу для пересечения дороги, с.
Длительность фаз светофорного регулирования определяется как решение задачи математического программирования, подробно описанной в работе [9]:
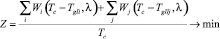 , (6)
, (6)
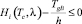 ,
, 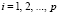 , (7)
, (7)
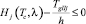 ,
, 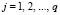 , (8)
, (8)
где 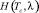 – функция восстановления, которая выражает количество автомобилей, прибывающих к перекрестку за время Tc,
– функция восстановления, которая выражает количество автомобилей, прибывающих к перекрестку за время Tc,
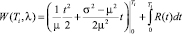 – средняя задержка за цикл регулирования [9].
– средняя задержка за цикл регулирования [9].
Численное решение задачи (6–8) находится, например, с помощью систем Maple или MatLab.
Стратегия A2. В случае использования жесткого режима регулирования без выделения отдельной фазы для пешеходного потока параметр Tserv вычисляется аналогично пункту 2.1 по формуле (5). Однако при расчете длин циклов светофорного регулирования в задаче математического программирования целевой функцией будет следующая:
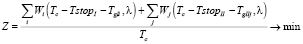 , (9)
, (9)
TstopI и TstopII – среднее время, необходимое автотранспорту для пропуска пешеходов через дороги I и II соответственно, с,
TgIi – разрешено движение на дороге I в i-ом направлении, с,
TgIIi – разрешено движение на дороге II в j-ом направлении, с.
λ – множество параметров обобщенного закона Эрланга для транспортных потоков.
Отметим, что в стратегиях A1 и A2 для каждого состояния Qi вычисляется оптимальный цикл светофорного регулирования, который зависит от интенсивности всех конфликтующих на перекрестке потоков.
Стратегия A3. В случае применения вызывных устройств для пешеходов среднее время, необходимое пешеходу для пересечения перекрестка, можно расчитывать так, как предлагается в работе [10]:
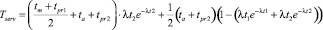 , (10)
, (10)
где tpr1 – переходный интервал между сигналами, с.,
tpr2 – зеленый сигнал, с,
ta – зеленый сигнал для транспорта минимальной длительности, с,
tm – период горения мигающего зеленого сигнала в пешеходной фазе, с,
λ – параметр показательного распределения плотности пешеходного потока.
Формула (10) выведена в предположении, что пешеходный поток, прибывающий к перекрестку, распределен по показательному закону. Предполагается полное подчинение пешеходов сигналам светофора. При расчетах применялись свойства числовых характеристик случайных величин.
Выше рассмотрены три основных варианта схемы организации движения на перекрестке. Однако возможно расширять количество стратегий Ai. Например, для отдельных перекрестков есть смысл добавить вариант нерегулируемого пересечения. Кроме того, количество фаз цикла светофорного регулирования также можно варьировать, что в свою очередь увеличит количество возможных стратегий игрока A.
Стратегии «природы» в работе – это распределение интенсивностей автотранспорта по полосам и интенсивность пешеходного потока, прибывающего к перекрестку через определенные промежутки в течение небольшого периода времени. В этом случае применяются прогнозные модели для формирования базы исходных данных для TIMeR_Mod. Однако возможно составление платежной матрицы для периода длиной, например, в сутки. Тогда придется брать статистические данные для составления матриц ASTREETS и BINTERSECTION.
Заключение
В работе решена задача определения того варианта организации движения на перекрестке, который за рассматриваемый промежуток времени обеспечивает оптимальную интенсивность обслуживания пешеходов. Причем благодаря возможности выбирать с помощью модели TIMeR_Mod оптимальные циклы регулирования при изменении распределения интенсивностей в транспортных и пешеходных потоках с течением времени, учитываются интересы всех конфликтных сторон: автотранспортных потоков и пешеходов.
Рассмотренная проблема является актуальной в настоящее время и требует математически обоснованного решения. Предложенный метод организации движения пешеходного потока на перекрестке позволит сделать оптимальный выбор в условиях неопределенности в соотношениях между величиной пешеходного и автотранспортного потоков на конкретном перекрестке.
Библиографическая ссылка
Наумова Н.А., Данович Л.М., Тесленко Н.Ф. МЕТОД ОПРЕДЕЛЕНИЯ ОПТИМАЛЬНОЙ ОРГАНИЗАЦИИ ПЕШЕХОДНОГО ДВИЖЕНИЯ НА ПЕРЕКРЕСТКЕ // Современные наукоемкие технологии. 2018. № 9. С. 76-80;URL: https://top-technologies.ru/ru/article/view?id=37163 (дата обращения: 12.02.2026).



