Тепловая модель тепловых процессов в технических системах (ТС), основанная на концепции системы изотермических тел [1], находящихся в тепловом взаимодействии между собой и окружающей средой, является в настоящее время наиболее универсальным и эффективным методом теплового моделирования. В этой концепции объемная конструкция ТС и протекающие в ней тепловые процессы представляются направленным графом, содержащим N узлов, моделирующих изотермические тела, и M ветвей, моделирующих теплообмен между ними и окружающей средой. В состав ветвей тепловой модели могут входить элементы с тепловыми проводимостями, теплоемкостями, внешними зависимыми и независимыми источниками тепловых потоков. С помощью тепловой модели естественным образом моделируются ТС любой сложности и пространственной конфигурации, стационарные, нестационарные и нелинейные тепловые процессы со сложным теплообменом (кондукцией, конвекцией и излучением), включая различные физические эффекты, такие, например, как тепловая обратная связь в ТС, интервально-стохастическая неопределенность факторов теплообмена, течение жидкостной и воздушной среды в ТС.
Математическая модель, описывающая нестационарные, нелинейные тепловые процессы в ТС, представленной тепловой моделью, представляет собой матричное дифференциальное уравнение в обыкновенных производных первого порядка [1]:
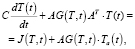
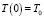, (1)
где T(t) – N-вектор-столбец искомых нестационарных температур в узлах графа тепловой модели ТС; A – N×M-матрица инциденций графа тепловой модели; G – M×M-диагональная матрица тепловых проводимостей ветвей графа тепловой модели; C – N×N-диагональная матрица тепловых емкостей изотермических элементов тепловой модели; J – N-вектор независимых источников тепловых потоков в тепловой модели; Ta – N-вектор-столбец известных температур в узлах графа тепловой модели; T0 – N-вектор начальных температур в узлах графа тепловой модели.
Стационарные и нелинейные тепловые процессы в тепловой модели ТС описываются математической моделью в виде системы нелинейных алгебраических уравнений
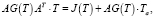(2)
а линейные тепловые процессы, с независящими от температуры проводимостями в матрице G и независимыми источниками тепловых потоков векторе J, – математической моделью в виде системы линейных алгебраических уравнений
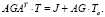(3)
Решение матричных уравнений (2) или (3) относительно неизвестного вектора температур T, как правило, осуществляется методом итерации. Для применения итерационного метода исходную систему уравнений предварительно подготавливают, разлагая диагональные элементы hii (i = 1, 2, …,N) матрицы H = AGAT на сумму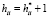 
, так что матрица H становится равной H = H* + I с единичной диагональной матрицей I. Тогда исходная система (2) или (3) приводится к удобному для итерационного метода виду, а именно, к T = –H*•T + J + AG•Ta. Вместе с тем теорема сходимости процесса итерации [2] накладывает довольно жесткие ограничения на матрицу H*, требуя выполнение соотношения 
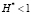для какой-либо из ее норм 
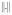, которое довольно редко выполняется на практике и чаще вообще не выполняется. Поэтому разработка методов решения как линейных, так и в особенности нелинейных систем уравнений, свободных от подобного рода требований, чрезвычайно актуальна.
Цель исследования: разработка метода, позволяющего определять решение как линейных, так и нелинейных систем алгебраических уравнений вида (2) и (3), моделирующих тепловые процессы в технических системах с приемлемой для практики точностью [3]. Метод основан на так называемом псевдорешении и псевдообратной матрице [4, 5], которое дает решение хотя и приближенное, однако наилучшее в смысле минимума суммы квадратов невязки правой и левой частей уравнений. Применение метода псевдорешения в рассматриваемом случае оказывается возможным ввиду специального вида исходной матрицы системы, а именно, H = AGAT. Представление матрицы тепловой и математической моделей теплообмена как H = AGAT позволяет применить к поиску решения системы уравнений аппарат псевдообратной матрицы, оказавшийся чрезвычайно гибким и эффективным. Его применение позволяет моделировать тепловые процессы в сложных конструкциях электронных систем [6], стохастические процессы теплообмена [1] и учитывать воздействие эффекта тепловой обратной связи в ТС.
Метод псевдообратной матрицы и псевдорешения
Рассмотрим матричное нелинейное алгебраическое уравнение (2). Умножим обе его части слева на транспонированную матрицу инциденций AT, получим
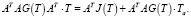(4)
Матрица B = ATA равна произведению двух прямоугольных матриц, M×N-матрицы AT и N×M-матрицы A, причем для тепловых моделей реальных ТС выполняется соотношение N < M. Ранг матрицы B равен r = min{N, M} и ее представление в виде произведения двух прямоугольных матриц AT и A является ее скелетным разложением [5]. Поскольку ранг квадратной матрицы B удовлетворяет условию r < M, то матрица B является вырожденной и, следовательно, обратной матрицы не имеет. Вместе с тем существует ее псевдообратная матрица B+, обладающая тем замечательным свойством, что для системы уравнений Bx = y (x и y – N-векторы) с прямоугольной или вырожденной матрицей B норма невязки
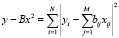
достигает своего наименьшего среди всех других векторов X значения на, так называемом псевдорешении X+ = B+Y, выражающемся через псевдообратную матрицу B+, причем вектор X имеет при этом и наименьшую длину [4, 5].
Если для вырожденной матрицы B построено ее скелетное разложение B = ATA, то псевдообратная матрица B+, может быть выражена в виде [4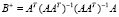, 5]
. (5)
Тогда уравнение (4) запишется как
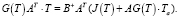(6)
Матрица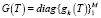 
, будучи диагональной, имеет обратную диагональную же матрицу, с легко вычисляемыми элементами, то есть 
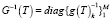. Умножая обе части матричного выражения (6) слева на обратную матрицу G-1(T), получим
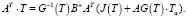(7)
Умножим теперь обе части матричного выражения (7) слева на матрицу A. Матрица C = AAT является квадратной, симметричной и невырожденной, поскольку ее ранг r = N совпадает с ее размерностью и, следовательно, матрица C = AAT имеет обратную матрицу C-1 = (AAT)-1. Заметим, что матрица инциденций A не зависит от температуры и состоит только из элементов 0, +1 и –1.
Окончательное явное псевдорешение T+ уравнения (7) будет равно
,
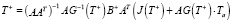или после подстановки в него выражения (5) для псевдообратной матрицы B+, искомое псевдорешение составит
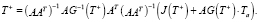
Учитывая, наконец, что вид матрицы C = AAT, получим окончательно:
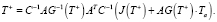(8)
Преимущество определения псевдорешения T+ (8) перед обычным решением T = H-1•(J(T) + AG(T)•Ta), следующим из (4), состоит в том, что во втором случае требуется постоянное обращение матрицы H-1 = (AG(T)AT)-1 при различных значениях температур T, в то время как в первом случае требуется только вычисление диагональной обратной G-1(T), записанной в явном виде относительно температур T, элементы которой легко вычисляются.
Оценка адекватности псевдорешения и сравнение с точным
Проведем оценку и сравнение обычного и псевдорешения между собой и рассмотрим для этого матричное уравнение AGAT•x = y для двух конкретных случаев.
A) Матрицы и векторы рассматриваемой системы уравнений AGAT•x = y равны
, 
, 
.
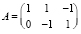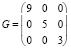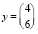Точное решение уравнения AGAT•x = y и псевдорешение, вычисленное согласно полученному выражению (8), а именно,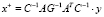 
равны соответственно
, 
.
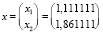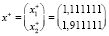Сравнение точного x и псевдорешения x+ показывает их практически полное совпадение: первые элементы решений равны 1,111111 и совпадают полностью, а вторые элементы x2 = 1,861111 и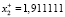 
различаются между собой с абсолютной погрешностью Δ = 0,05 и относительной погрешностью δ = 2,7 %.
B) Матрицы и векторы уравнения AGAT•x = y равны
, 
,
.
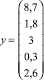Точное решение равно:
,
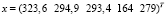псевдорешение:
.
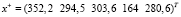Сравнение точного и псевдорешений между собой показывает, что
– вектор абсолютных погрешностей составляет
,
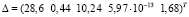– вектор относительных погрешностей
, %.
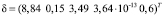Значения относительных погрешностей сравнения точного и псевдорешения показывают, что они не превышают величины 8,9 %, что находится в пределах допускаемых при инженерных расчетах тепловых режимов ТС.
Выводы
В работе предложен новый метод моделирования и анализа тепловых процессов в сложных технических системах. Математической моделью тепловых процессов в стационарном случае являются системы алгебраических уравнений: нелинейных для температурозависимых процессов теплообмена и линейных в случае их независимости от температуры. Созданию нового метода решения уравнений математической модели и посвящена данная статья.
Разработанный здесь метод позволяет определять решение как линейных, так и нелинейных систем алгебраических уравнений математической модели (2) и (3) с приемлемой для практики точностью. Метод основан на псевдорешении матричных уравнений и псевдообратной матрице, которое определяет приближенное решение, которое является наилучшим с точки зрения критерия минимума суммы квадратов разности между правой и левой частями матричных уравнений модели. Возможность применения метода псевдорешения и псевдообратной матрицы в рассматриваемом случае обусловливается специальной структурой исходной матрицы системы уравнений, имеющей вид H = AGAT, в котором матрица A и транспонированная ей матрица AT является матрицей инциденций графа тепловой модели, а матрица G – диагональной матрицей тепловых проводимостей тепловой модели. Представление матрицы тепловой и математической моделей, представляющих тепловые процессы в технической системе как H = AGAT, делает возможным применение аппарата псевдообратной матрицы к поиску решения системы уравнений. Этот подход показал свою гибкость и эффективность, а также многофункциональность, позволяющую моделировать тепловые процессы в сложных конструкциях электронных систем, стохастические процессы теплообмена и учитывать при этом воздействие эффекта тепловой обратной связи в электронных и микроэлектронных системах.
Отметим также, что норма матрицы H* в разложении исходной матрицы H = AGAT системы уравнений H = H* + I, необходимом для проведения итерационного процесса при определении решения системы уравнений H•x = y в первом из рассмотренных случаев равна 21, а во втором – 1,6. Иначе говоря, требование чтобы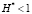 
, необходимое для сходимости итерационного процесса, не выполняется, что свидетельствует о том, что применение метода итераций для решения матричных уравнений (2) и (3) математической модели, в обоих рассмотренных случаях невозможно.
Сравнение точного и псевдорешения общей линейной системы уравнений AGAT•x = y на конкретных примерах показывает, что наибольшее значение относительной погрешности составляет 8,9 % и находится в пределах – не более 15 % – допускаемых при инженерных расчетах тепловых процессов технических систем.
Библиографическая ссылка
Мадера А.Г. АНАЛИЗ ТЕПЛОВЫХ ПРОЦЕССОВ В ТЕХНИЧЕСКИХ СИСТЕМАХ МЕТОДОМ ПСЕВДООБРАТНОЙ МАТРИЦЫ // Современные наукоемкие технологии. – 2018. – № 9. – С. 61-65;URL: https://top-technologies.ru/ru/article/view?id=37160 (дата обращения: 04.12.2024).