В настоящее время в промышленном производстве всё большее распространение получает концепция так называемого индустриального (или «промышленного») Интернета вещей (Industrial Internet of Things, IIoT), под которым понимается интернет вещей для корпоративного/ отраслевого применения. Реализация данной концепции предполагает развертывание в рамках предприятия (корпорации) системы объединенных компьютерных сетей и подключенных промышленных (производственных) объектов со встроенными датчиками и ПО для сбора и обмена данными, с возможностью удаленного контроля и управления в автоматизированном режиме, без участия человека [1].
Одной из особенностей функционирования подобных систем является необходимость обработки значительных объемов неструктурированных данных, их фильтрации и адекватной интерпретации, что является приоритетной задачей для предприятий.
Для выполнения функций обработки неструктурированных данных в рамках реализации концепции промышленного Интернета вещей в рамках распределенной автоматизированной системы управления предприятием (АСУП) реализуется технология Web Mining – использование методов Data Mining для исследования и извлечения информации из Web-документов и сервисов [2].
Цель исследования: при создании эффективных подсистем поиска и обработки неструктурированной информации в рамках АСУП промышленного Интернета вещей, реализующих технологию WebMining разработчики могут столкнуться с проблемами, аналогичными проблемам, характерным для работы с информацией в сети Интернет, а именно:
1. Поиск значимой информации. Зачастую множество ссылок, предоставляемых поисковыми системами, только незначительный процент предоставляет релевантную информацию; кроме того, поиск неиндексированной информации затрудняется за счет низкой повторяемости вызовов.
2. Создание новых знаний вне полученной из поисковой системы информации.
3. Персонализация информации.
4. Изучение потребителя или индивидуального пользователя (необходимости персонализации поисковых систем) [3].
Проведем краткий обзор наиболее известных математических методов извлечения контента из массивов неструктурированной документированной информации.
Метод TFIDF
Данный метод предполагает использование двух понятий (метрик):
1. Частота термина TF (term frequency), определяемая как отношение количества выявлений некоторого термина к общему количеству слов документа. Данная метрика позволяет оценить вестермина ti в пределах отдельного документа:
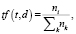(1)
где ni – количество вхождений i-го термина в документ,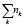 
– общее количество слов в данном документе, включающее общеупотребительные и связующие слова [4].
2. «Инвертированная частота документа» IDF (inverse document frequency) инверсия частотности встречаемости заданного термина встречается в документах массива, позволяющая снизить веса связующих и общеупотребительных слов. Для каждого уникального слова в пределах конкретной коллекции документов существует только одно значение IDF 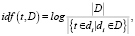(2):
(2)
где |D| – количество документов массива,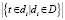 
– количество документов в массиве D, в которых встречается t.
Таким образом, мера TF-IDF определяется по следующей формуле:
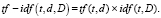(3)
При использовании данной меры максимальный вес получают термины с высокой частотой в пределах одного документа и с низкой частотой употреблений в других документах [4].
Известны также различные модификации модели tf-idf. Одним из примеров является мера Okapi BM25 [5]. Наиболее существенным ограничением использования tf-idf является необходимость неизменности набора данных в течение всего времени расчета, что значительно усложняет вычисления, если требуется их проведение в режиме реального времени.
Скрытые марковские модели
Рассмотрим формальное описание скрытой марковской модели (СММ).
Каждая модель определяется следующими параметрами:
1. Множество S = {s1, s2, …, sN} из N состояний.
2. Начальное распределение вероятностей P = {pi}.
3. Матрица вероятностей переходов между состояниями A = {ai}.
4. Матрица вероятности генерации наблюдений B = {bj(Ot)}, где bj(Ot) – вероятность генерации наблюдения Ot в момент времени t в состоянии qt = sj, bj(Ot) = P(Ot|qt = sj).
Представленная таким образом модель является одномерной, но для поиска и обработки документированной информации интерес представляют псевдомногомерные СММ, состоящие из конечного количества элементов, называемых суперпозициями, каждый из который в свою очередь представляет собой отдельную СММ [6].
В рамках функционирования автоматизированной поисковой системы, использующей СММ, документ может быть представлен в форме случайного n-мерного дискретного сигнала, обладающего n признаками, образующими индекс. В свою очередь индекс (вектор-документ) может извлекаться из документа различными способами, такими как преобразование Карунена – Лоэва [7].
Полученные вектор-документы распределяются по состояниям модели, определяющим некоторые ключевые признаки поиска. Например, СММ, реализующая поиск журнальных статей, может состоять из шести суперсостояний, соответствующих параметрам статьи (Название, автор(ы), наименование журнала, год, номер, ISBN), каждое из которых делится на отдельные состояния.
В данном разрезе поиск документов основывается на выявлении схожести в многомерном пространстве. Мерой схожести является функция, определяющая значение схожести между двумя или более объектами на основе некоторых предопределенных критериев или метрик. Под метрикой понимается функция расстояния r, определенная на метрическом множестве, для любых точек a, b, c которого верна следующая система условий:
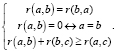(4)
Рассмотрим процесс поиска информации следующим образом.
Пусть O – объект массива, L – объект запроса, K – ключевые документы, r – метрики. На основе (1) можно утверждать истинность следующих неравенств:
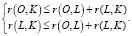(5)
Соответственно, расстояние от объекта запроса до объекта массива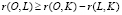 
.
Таким образом, путем последовательного сравнения объектов массива и запроса с ключевым объектом, может быть выделена нижняя граница метрик схожести между документом и запросом, позволяющая отсечь ту часть массива документов, которая не удовлетворяет запросу.
Первое представление математической модели, для формализованного представления задачи поиска и обработки информации в рамках концепции промышленного интернета вещей – математическая модель ссылочного ранжирования [8]. Рассмотрим web-документы и ссылки на них в виде графа, в котором документы являются вершинами, а ссылки – дугами графа. Пусть G(V, E) – ориентированный граф, где V – множество вершин, а E – множество дуг. ОСИ можно представить в виде разреженной матрицы S – матрицы смежности графа G, состоящей из элементов (2.1)
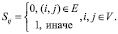(5)
В матрице могут одновременно присутствовать ссылки как вида (i, j), так и (j, i). Пусть Θ – некое множество тематик, T(i, j, t) – функция веса ссылки (j, i) в тематике t∈Θ (так называемого тематического веса), deg(i, t)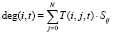
– сумма весов всех исходящих ссылок i-й вершины в тематике t, 
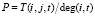– вероятность перехода пользователя по ссылке (i, j). Матрица тематических весов для ссылок (i, j) может быть записана в следующем виде:
.
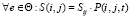Таким образом, тематическое ранжирование i-й вершины может быть представлено в виде системы итерационных линейных алгебраических уравнений:
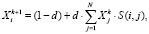
где d – коэффициент затухания, k – номер итерации,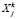 
– значение ранга j-й вершины в ходе k-й итерации k.
Второе математическое представление задачи поиска и обработки неструктурированной документированной информации – модель индексации документов
Математическая модель индексации может быть сформирована в виде
,
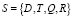где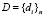 
– множество документов в массиве,
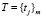– множество терминов, индексирующих смысловую нагрузку документов,
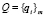– множество запросов пользователей либо операторов систем,
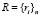– множество выданных в результате поиска ссылок на документы,
n, m – соответственно количество документов в массиве и используемых терминов.
Если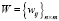 
– матрица, определяющая отношения терминов к документам, где wij – вес j-го термина в i-м документе с учетом всех документов, для которых 
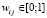, то wij = 0, если j-й термин не встречается в i-м документе; наоборот wij = 1, когда j-й термин 100 % соответствует i-му документу.
Работа информационно-поисковой системы (ИПС) может быть определена как вычисление вектора ответа R = W•Q путем преобразования вектора запроса Q в соответствии с матрицей W.
Для реализации преобразования необходимо произвести определение весовых коэффициентов терминов. Данное определение может быть представлено в виде следующего алгоритма:
1. Производится определение веса j-го термина для i-го документа. Обозначим её как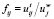 
, где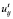 
– общее число выявленных появлений j-го термина в i-м документе, 
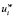– общее количество слов в i-м документе. Тогда fij – коэффициент веса j-го термина в i-м документе без учета остального массива (в случае, когда данный коэффициент максимален для j∈[1, N], j-й термин определяется как отражающий содержание i-го документа.
2. Производится определение общего веса j-го термина в рамках всего массива документов. Сравнивая соотношение общего количества документов в массиве n и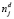 
– количество документов, в которых встречается j-й термин (так называемая документная частота), можно определить, является ли слово значимым термином для данного документа (чем меньше значение 
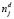, тем большим весом может обладать j-й термин в документе). Для нормализации возможно проведение операции натурального логарифмирования n и 
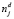. Таким образом, обратная документная частота определяется как 
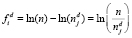[9].
Общий вес j-го термина в i-м документе вычисляется как
.
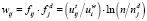Таким образом, можно говорить о сосредоточении j-го термина в i-м документе при повышении его частоты в данном документе и снижения количества документов, содержащих j-й термин.
На основе приведенного метода возможно построение матрицы отношений W, которая является основой базы индексов информационно-поисковой системы.
Третье представление – формализация обработки неструктурированных данных веб-документов.
Данная задача может быть сформулирована следующим образом: Имеется множество веб-ориентированных документов P = {p1, p2,…, pn}, каждый из которых определяется набором признаков (переменных) pj = {x1, x2,…, xm,y}, где xm – блок информации, содержащейся в документе, определяющей значение переменной y – значение интересующей пользователя информации, очищенной от шума [10].
В свою очередь каждая переменная xm может принимать значения из некоторого множества Z = {z1,z2,…}. Таким образом, конечное множество выделенных из неструктурированного массива релевантных данных, очищенных от шумов, над которыми возможны дальнейшие действия по структуризации, определяется как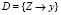 
.
Заключение
Представленные формализованные представления являются основой для дальнейшей разработки методов и алгоритмов обработки неструктурированной информации в распределенных АСУП, ориентированных на работу в условиях предприятий, реализующих концепцию промышленного Интернета вещей. На основе разработанных представлений предполагается создание и программная реализация модуля интегрированной корпоративной информационной системы для управления цифровым предприятием с распределенными информационными массивами.
По результатам предварительных прогнозов можно предполагать повышение эффективности работы программных модулей, использующих реализацию разработанных формализованных представлений, в среднем на 7–10 % по сравнению с существующими системами поиска и обработки неструктурированной информации.
Кроме того, существуют практические перспективы применения результатов разработки в области Web Mining для создания программных средств извлечения неструктурированной информации с веб-страниц.
Библиографическая ссылка
Гагарина Л.Г., Слюсарь В.В., Федоров А.Р., Федоров П.А. РАЗРАБОТКА МАТЕМАТИЧЕСКОЙ МОДЕЛИ ПРОЦЕССА ПОИСКА И ОБРАБОТКИ НЕСТРУКТУРИРОВАННОЙ ДОКУМЕНТИРОВАННОЙ ИНФОРМАЦИИ // Современные наукоемкие технологии. – 2018. – № 9. – С. 41-44;URL: https://top-technologies.ru/ru/article/view?id=37156 (дата обращения: 20.04.2024).