Проблема оптимизации является одной из важнейших задач в различных направлениях как научной деятельности, так и повседневной человеческой жизни. Проектирование сложных динамических систем сопровождается поиском оптимальных значений параметров, что связано с такими трудностями, как многопараметричность, нелинейность и мультимодальность целевой функции и др. [1]. Для решения подобных задач существует целый ряд методов, среди которых особое место занимают эвристические алгоритмы оптимизации [2].
Целью данной работы является разработка эффективного модифицированного генетического алгоритма дуэлей путём введения расширенных генетических операторов в классический алгоритм дуэлей.
Алгоритм дуэлей
Работа алгоритма дуэлей начинается с этапа регистрации агентов-дуэлянтов, представляющих собой набор боевых навыков – массив бинарных строк (хромосом); каждая бинарная строка задаёт одну из координат предполагаемого оптимума. Изначально дуэлянты формируются случайно. Далее они оцениваются функцией приспособленности, отбираются чемпионы – несколько агентов с лучшими результатами, после чего составляется расписание дуэлей – таблица, где каждому дуэлянту сопоставляется один соперник. В дуэли побеждает тот, чья приспособленность в сумме со случайным числом больше. Боевая сила дуэлянта описывается формулой:
F(xi) = Fitness(xi) + (Upp – Low)*rand,
где Upp и Low являются значениями соответственно верхней и нижней границы пространства поиска, Fitness(xi) – значение приспособленности, rand – число ∈ [0,1].
Далее победители подвергаются мутации, в результате случайным образом изменяются наборы их навыков. Проигравшие агенты обмениваются с победителями участками хромосом из набора навыков – подвергаются скрещиванию. После этого происходит переоценка приспособленности всех участников: худшие заменяются предварительно отобранными чемпионами. В случае появления дуэлянтов с более высокими показателями приспособленности, чем у текущих чемпионов, происходит переобъявление чемпионов [3].
Кодирование. Для представления вещественных координат агентов в формате двоичных чисел было использовано прямое кодирование чисел в двоичное представление с предварительным масштабированием величин.
Параметр ChromosomeLength определяет длину хромосом и соответствует наибольшему натуральному числу, удовлетворяющему отношению
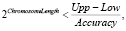
где Accuracy определяет точность дробной части и принадлежит интервалу (0,1).
Изначально популяция формируется случайным образом: находится разность верхней и нижней границы (Upp и Low), составляющих отрезок поиска для координаты, и умножается на случайное вещественное число, ограниченное отрезком [0…1]. Полученное значение суммируется с нижней границей (Low) и конвертируется в бинарное представление. Процесс конвертации заключается в предварительном преобразовании числа в равномерно распределённое значение, которое определяется как
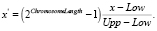
Полученное десятичное вещественное число x′ конвертируется в двоичное число. Для обратного преобразования числа из двоичного получаем десятичное x' и находим соответствующее немасштабированное число x посредством формулы
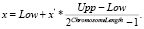
Масштабирование дает возможность распределить все числа в бинарном представлении равномерно от 00…0 до 11…1, что позволяет свободно применять операторы, изменяющие двоичные хромосомы, получая без каких-либо смещений значения, удовлетворяющие пространству поиска.
Генетические операторы
Метаэвристический алгоритм дуэлей основывается на некоторых операторах генетического алгоритма, а именно: одноточечном скрещивании и мутации инверсией гена. В связи с этим в работе рассмотрена возможность создания нового модифицированного генетического алгоритма дуэлей путём применения других видов операторов скрещивания и мутации, а также введением оператора селекции. Были предложены и исследованы следующие генетические операторы: одноточечное, двухточечное, триадное, однородное и перетасовочное скрещивания, мутация методами плотности, инверсией гена, перестановкой, а также селекция методом усечения, вытеснения и элитарный отбор [4–6].
Скрещивание. Этап скрещивания победителей и проигравших подобен кроссинговеру в генетическом алгоритме [7]. Так как получаются два потомка, то среди них выбирается лучший, который и заменяет проигравшего, участвующего в скрещивании. Наиболее значимыми являются следующие виды данного оператора:
1) Одноточечный: агенты обмениваются участками хромосом, образуя двух потомков. В предложенной программной реализации точкой перекрёста принимается середина хромосомы.
SubLen = ChromosomeLength/2,
где SubLen – длина обмениваемой области.
2) Двухточечный: длина обмениваемой области равна трети от длины хромосомы.
3) Однородный: создаётся бинарная маска, каждый ген которой определяет, от какого родителя (победителя или проигравшего) наследник получит соответствующий ген. То есть если маска представлена последовательностью 011, то первый ген наследника будет взят от победителя, а оставшиеся гены от проигравшего.
4) Триадный: метод аналогичен однородному, но маской является не случайная двоичная последовательность, а случайная особь из популяции.
5) Перетасовочный: победитель и проигравший предварительно обмениваются участками хромосом в случайной точке перекрёста, после чего происходит ещё одно их конечное скрещивание: обмен участками, разделёнными пополам, что и даёт двух потомков [8].
Мутация. Ко всем победителям применяется оператор мутации [9], представленный следующими вариантами:
1) Инверсия гена: инвертируется случайный ген хромосомы.
2) Плотность мутации: существует вероятность мутации не только для целой особи (первая ступень), но и вероятность второй ступени, где каждый ген каждой хромосомы особи с определённой вероятностью подвергается оператору инверсии.
3) Перестановка: выбирается случайный ген хромосомы, соседние особи которого меняются местами.
Селекция. Стоит заметить, что на этапе скрещивания при тренировке проигравших дуэлянтов из двух полученных «потомков» в дальнейшем использовался лишь один. Поэтому в новый модифицированный генетический алгоритм дуэлей было предложено ввести новый этап – оператор селекции, который заключается в том, что оба потомка вместе с подвергшимися мутации победителями помещаются в одну популяцию, из которой затем отбираются дуэлянты в конечную популяцию, соразмерную начальному набору. Выборка особей в новую популяцию может быть осуществлена посредством следующих методов:
а) отбор усечением: все особи сортируются по убыванию приспособленностей, после чего в отборе принимают участие лишь те дуэлянты, индекс которых удовлетворяет заданному порогу из отрезка [0,1]. Из тех, кто принимает участие в конечном отборе, выбирается случайным образом одна особь, попадающая в новую популяцию;
б) элитарный отбор: из имеющихся отсортированных особей выбирают n лучших, где n – количество дуэлянтов в начальном наборе;
в) отбор вытеснением: выбор особи зависит не только от показателя приспособленности, но и от наличия в составляемой новой популяции особей со схожим хромосомным набором [10].
Исследование модификаций метода дуэлей
Для проведения исследований были выбраны следующие целевые функции: Михалевича, Растригина, Де Джонга, Янга, кубическая, Швефеля, Розенброка (количество параметров оптимизируемых функций равно 10).
В качестве базовых операторов использованы мутация инверсией гена (с вероятностью 0,2), одноточечное скрещивание и селекция усечением.
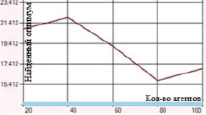
Наибольшие погрешности были отмечены в случаях оптимизации функций Розенброка и Растригина. Представленные на рис. 1–2 графики отражают зависимость находимого алгоритмом дуэлей оптимума от числа агентов в диапазоне от 20 до 100 с шагом агентов равным 20.
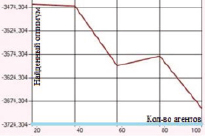
а) Функция Швефеля. Поиск в отрезке [–500; 500] при 1000 итераций
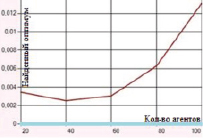
б) Функция Де Джонга. Поиск в отрезке [–5; 5] при 100 итераций
Рис. 1. Зависимость величины найденного оптимума от количества агентов для функций Швефеля и Де Джонга
а) Функция Растригина. Поиск в отрезке [–5; 5] при 2500 итераций
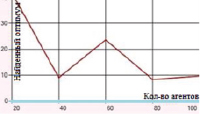
б) Функция Розенброка. Поиск в отрезке [–5; 5] при 5000 итераций
Рис. 2. Зависимость величины найденного оптимума от количества агентов для функций Растригина и Розенброка
Протестируем алгоритм дуэлей на задаче Растригина с различными комбинациями генетических операторов. При тестировании на поиск выделяется 2500 итераций, чтобы алгоритм давал погрешности, не успевая найти оптимальные решения, и, соответственно, удобнее было отслеживать изменения эффективности поиска.
В случае одноточечного скрещивания при использовании метода плотности мутации заметно снижается значение погрешности: в целом абсолютная ошибка ниже 1 единицы; минимальное отклонение, равное 0, достигается при вероятности метода плотности равной 0,5; результаты для разных значений вероятностей представлены в таблице и на рис. 3. Мутация инверсией гена характеризуется отклонением от глобального оптимума в 17–22 единицы. В случае одноточечного скрещивания и мутации перестановкой гена погрешность также достаточно высока (10–24 единицы).
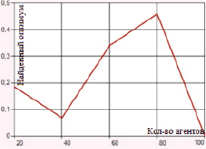
а) Одноточечное скрещивание с мутацией методом плотности (вероятность 0,5)
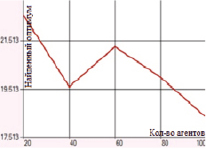
б) Одноточечное скрещивание с мутацией инверсией гена
Рис. 3. Зависимость величины найденного оптимума от количества агентов для функции Растригина при одноточечном скрещивании
Погрешность для метода плотности мутации
|
Вероятность мутации в методе плотности |
Отклонение от глобального оптимума |
|
0,1 |
0,7–1,8 |
|
0,3 |
0,07–0,4 |
|
0,5 |
0–0,45 |
|
0,7 |
0,07–0,6 |
|
0,9 |
0,35–1,1 |
Для варианта с комбинацией двухточечного кроссинговера и мутации инверсией гена наблюдается ситуация, аналогичная набору «мутация инверсией – одноточечное скрещивание» – погрешность 18–23. Переход к методу плотности мутации незначительно изменяет результат в лучшую сторону, погрешность полученных алгоритмом решений для различных значений вероятности мутации методом плотности в целом неизменно находится в диапазоне 10–21 единицы. Применение метода мутации перестановкой гена с двухточечным кроссинговером приводит к существенному росту ошибки (25–45 единиц). Таким образом, для двухточечного скрещивания минимальное отклонение от глобального оптимума так же, как и в случае одноточечного кроссинговера, достигается посредством использования метода плотности мутации.
При использовании однородного кроссинговера, как в комбинации с мутацией методом инверсии гена, так и с методом плотности мутации, алгоритм не находит точные значения оптимумов. Введение оператора перестановки гена значительных улучшений не даёт.
В случае триадного кроссинговера и мутации инверсией гена погрешность 17–48 единиц. При замене оператора мутации на метод плотности было замечено повышение эффективности поиска, ошибка в среднем принимает значения, принадлежащие диапазону 7–32 единицы. Однако при оптимальной комбинации параметров исследуемого алгоритма (20 агентов, вероятность плотности мутации 0,1) найденное решение отклоняется от глобального на 3 единицы.
Перетасовочное скрещивание с мутацией методом инверсии гена характеризуется погрешностью в 18–24 единицы. Подключение метода плотности мутации дает существенное снижение отклонения (в среднем принимает значения 0–3,5). Минимальная ошибка, равная 0, наблюдается, если значение вероятности мутации методом плотности лежит в диапазоне 0,5–0,7 (количество агентов равно 20) (рис. 4).
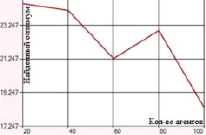
а) Перетасовочное скрещивание с мутацией инверсией гена
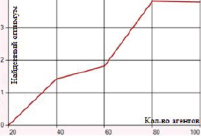
б) Перетасовочное скрещивание с мутацией методом плотности (вероятность 0,5)
Рис. 4. Зависимость величины возвращаемого оптимума от количества агентов для функции Растригина при перетасовочном скрещивании
Оптимальные результаты работы алгоритма обеспечивает следующая комбинация операторов: «перетасовочное скрещивание – мутация методом плотности». Кроме того, решения, близкие к оптимальным, достигаются на основе набора «одноточечное скрещивание – мутация методом плотности».
Проанализируем зависимость эффективности поиска от общей вероятности мутации для задачи Розенброка. В качестве применяемой модификации используем «перетасовочное скрещивание – метод плотности – отбор усечением».
При повышении вероятности выше 0,2 отмечается сильный рост погрешности. Вероятности 0,05; 0,1 и 1,5 не сильно отличаются от результатов вероятности 0,2, но происходит незначительное уменьшение количества аномалий (резких возрастаний погрешности), чаще возвращаемое решение оказывается глобальным оптимумом (погрешность 0 – в основном для вероятностей 0,05–0,1), но в среднем отклонение колеблется в диапазоне 3–6 единиц. При значениях вероятности меньше 0,05 погрешность возрастает: для 0,03 она составляет 70–100 единиц.
Заключение
Таким образом, в процессе проведенных исследований разработанного модифицированного генетического алгоритма дуэлей было установлено: модифицированный метод обладает высокой эффективностью по сравнению с классическим методом, что проявляется в повышении как точности поиска оптимальных значений целевых функций, так и скорости их нахождения. Предлагаемые модификации позволяют алгоритму наилучшим образом рассеиваться по пространству поиска, что позволяет избегать частого зацикливания в локальных экстремумах и гарантирует быстрый отбор эффективных решений. Наиболее эффективной модификацией предложенного алгоритма является набор из перетасовочного скрещивания, метода плотности мутации и отбора усечением.
Библиографическая ссылка
Частикова В.А., Митюгов А.И. РАЗРАБОТКА И ИССЛЕДОВАНИЕ МОДИФИЦИРОВАННОГО ГЕНЕТИЧЕСКОГО АЛГОРИТМА ДУЭЛЕЙ // Современные наукоемкие технологии. 2018. № 8. С. 144-149;URL: https://top-technologies.ru/ru/article/view?id=37135 (дата обращения: 21.12.2025).



