При изготовлении деталей различных механизмов и машин решаются две основные задачи: 1) обеспечение геометрической конфигурации детали (геометрический облик и точность), 2) обеспечение свойств материала детали (твёрдость, прочность, намагниченность и пр.) [1]. Учитывая, что для решения каждой из этих задач используются различные технологические приемы и процедуры, при проектировании технологии изготовления целесообразно рассматривать их как независимые задачи со своими специфическими особенностями. В статье рассматриваются вопросы, связанные с формированием геометрической конфигурации деталей.
Геометрия как наука появилась в древней Греции, ее основоположником считается Евклид, изложивший основные понятия и аксиоматику в своем труде «Начала». Развитием геометрии занимались многие ученые с древности. Так координатный метод Рене Декарта положил начало аналитической и дифференциальной геометрии. Задачи, связанные с архитектурой и черчением, привели Гаспара Монжа к созданию начертательной и проективной геометрии. Современная геометрия включает достаточно много разделов, в том числе и неевклидовы геометрии [2]. В современной интерпретации геометрия представляется как раздел математики, изучающий пространственные отношения и формы, а также другие отношения и формы, сходные с пространственными по своей структуре.
В статье рассматриваются проблемы, не разрешимые в рамках существующих геометрий, для решения которых предлагается в качестве базиса при описании геометрических объектов в трехмерном пространстве использовать шесть степеней свободы.
Проблемы описания геометрии реальных деталей
При изготовлении реальных деталей в машиностроительном производстве невозможно добиться абсолютной точности размеров. Поэтому для любого изготавливаемого объекта регламентируются пределы допускаемых погрешностей формы и взаимного расположения поверхностей, отображаемые на чертежах в виде так называемых полей допусков [3–5].
Первая проблема заключается в том, что существующие в геометрии инструменты формального описания оперируют с идеальными объектами и не могут описывать неидеальные (реальные) объекты. В качестве примера сопоставления идеальных и реальных объектов на рис. 1 рассмотрено расположение торцов двухступенчатого валика.
а) б)
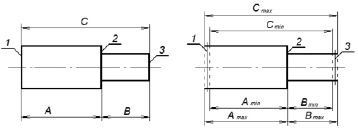
Рис. 1. Взаимное расположение поверхностей: а) идеальное; б) реальное
На рис. 1, а, показана «идеальная» модель вала. Указанные размеры задают взаимное расположение поверхностей вала в пространстве. Стоит отметить, что размер С получается в результате суммы размеров А и B. Иными словами, можно сказать, что расстояние между плоскостями 1 и 2 равно А, плоскостями 2 и 3 – B, а плоскостями 1 и 3 соответственно С = А + B [5].
Вторая проблема связана с возможностью описания только уже существующих геометрических конфигураций без учета схем и технологий их порождения. Это приводит к невозможности формальной проверки и оценки соответствия параметров детали функциональным требованиям, что в конечном итоге заканчивается либо некорректным, либо недостаточным представлением деталей (объектов) на чертежах и 3D моделях.
Изготовление детали зависит от применения определенного варианта технологии, в результате чего указанные выше размеры могут иметь различные значения. Например, в процессе изготовления детали величина размера А будет находиться в интервале между Amin и Amax (рис. 1, б). При выдерживании размера В его значение будет находиться в интервале между Bmin и Bmax. Тогда размер С получается автоматически и его значение находится в пределах между Amin + Bmin и Amax + Bmax. Предположим, погрешность точности размеров А и B в процессе обработки равна ± 0,1 мм, тогда погрешность размера С равна сумме погрешностей и составляет ± 0,2 мм.
Другой вариант изготовления данной детали может потребовать выдерживания размеров А и С. Тогда аналогичная погрешность этих размеров ± 0,1 мм, приведет к тому, что погрешность оставшегося размера В получится в пределах ± 0,2 мм.
Как видно из рассмотренного примера, реальные детали отличаются друг от друга в зависимости от вариантов изготовления или, иными словами, схемы порождения. Исходя из этого, можно сделать вывод о крайней необходимости разработки новой геометрии для описания реальных деталей: во-первых, для описания реальных объектов требуется нечеткая геометрия, учитывающая девиацию (колебания) размеров в регламентируемых пределах, во-вторых, геометрия должна описывать не только уже существующие объекты, но и способы или технологии их порождения. Далее авторы рассматривают возможность описания геометрической конфигурации объектов в шестимерном пространстве, где в качестве системы координат в трехмерном пространстве используются шесть степеней свободы.
Описание объектов в пространстве шести степеней свободы
В предыдущих работах авторов, например в [1] и других, неоднократно представлялась методика описания объекта (детали) в шестимерном пространстве степеней свободы. Набор степеней свободы в трехмерном пространстве авторы представляют единичным шестимерным вектором V с измерениями {Xl, Yl, Zl, Xα, Yα и Zα}. Предложенный авторами подход описывает состояние полной свободы элемента в трехмерном пространстве вектором Vа{0, 0, 0, 0, 0, 0}, а однозначно определенное положение – Vб{1, 1, 1, 1, 1, 1} [1].
Для описания технологии изготовления авторы считают, что деталь целесообразнее рассматривать не как твердое тело, а как некоторое замкнутое подпространство, которое ограничено набором элементарных бесконечно протяженных поверхностей, определенным образом взаимосвязанных между собой. Под элементарной поверхностью здесь понимается двумерное топологическое многообразие (двумерное пространство), образованное с использованием элементарных движений: прямолинейного перемещения вдоль координатной оси трёхмерного пространства (l), а также вращения вокруг координатной оси (a).
Ориентация элементарной поверхности в пространстве и придание ей определенного положения связано с лишением нужного количества степеней свободы [1, 6].
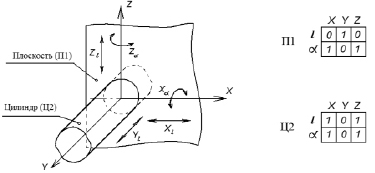
Для визуализации этой операции авторы разработали метод представления информации о наличии или отсутствии соответствующих степеней свободы в виде шестиклеточной таблицы, пример которой показан на рис. 2, где расположение плоскости и цилиндра представлено на рис. 2, а, а их табличное отображение – на рис. 2, б. Наличие степени свободы обозначено нулём, а единицей – её отсутствие.
а) б)
Рис. 2. Плоскость и цилиндр: а) расположение; б) табличное отображение
Если деталь представить в виде замкнутого подпространства, ограниченного совокупностью поверхностей, то технологический процесс изготовления детали описывает порождение форм поверхностей и их взаимного расположения.
Наиболее часто в машиностроении для формирования геометрической конфигурации детали используются так называемые элементарные поверхности: сфера, цилиндр, плоскость. Эти поверхности называются элементарными, так как могут быть получены сочетанием двух независимых простых производящих линий – прямой и окружности. Для субтрактивных технологий, особенно механической обработки, это существенно, поскольку технологическое оборудование способно выполнять два основных движения – перемещение (прямая) и вращение (окружность).
В подавляющем большинстве изготавливаемые на машиностроительных предприятиях детали формируются в виде совокупности отдельных простых геометрических форм: плоскость, цилиндр, шар. Соответственно геометрическая форма каждой детали определяется составом и взаимным расположением этих простых элементов [6]. Тогда поверхность детали также может быть представлена в виде совокупности элементарных поверхностей. Соответственно, процесс порождения детали может быть представлен как последовательность порождения элементарных поверхностей с учетом их взаимного расположения.
Формообразование элементарных поверхностей
Если представить поверхность как двумерное топологическое многообразие, то для ее порождения необходимы и достаточны две линии – образующая и направляющая. Используя разработанный авторами метод представления поверхностей в виде шестимерного вектора, легко получить нужные комбинации пары линий для порождения поверхностей. Для этого достаточно инвертировать вектор представления поверхности.
Например, для цилиндра (рис. 2) инвертирование его представления даст единицы в параметрах Yl, Yα, что соответствует прямой вдоль оси Y и повороту вокруг оси Y. Это означает, что данный цилиндр может быть получен перемещением прямой, параллельной оси Y по окружности вокруг оси Y или, наоборот, перемещением окружности, перпендикулярной оси Y вдоль прямой, соответствующей оси Y [7]. Так может быть получена любая из элементарных поверхностей, что показывает практическую значимость предложенного подхода для формализации образования поверхностей детали.
Взаимное расположение элементарных поверхностей
Взаимное расположение поверхностей определяется системой установленных размеров и допусков. Для описания состава и расположения поверхностей авторы предлагают сгруппировать всю информацию в виде трех множеств: множества поверхностей (S), множества связей между поверхностями (R) и множества параметров (P), характеризующих свойства этих поверхностей и связей. Тогда геометрическая конфигурация может быть представлена в виде структуры, содержащей элементы этих трех множеств.
Описания и операции со структурами удобно выполнять в терминах теории графов. Поэтому для формализации информации о конфигурации детали авторы воспользовались инструментами теории графов. В данном случае геометрическая конфигурация детали может быть представлена в виде графа G (S, R), где множество вершин S:={s1, s2, …, sn} представляет множество поверхностей, а множество ребер R:={r1, r2, …, rn} соответствует множеству связей между поверхностями [5].
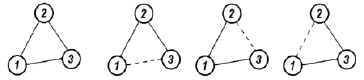
Связи между поверхностями, указанные в графе, можно использовать для представления размерных цепей. Так, для детали, изображенной на рис. 1, можно рассмотреть несколько вариантов размерных связей (рис. 3). Плоским поверхностям торцов детали (1, 2, 3) поставлены в соответствие вершины графа, а заданным размерам (А, B, С) – ребра. Для «идеальной» модели вала (рис. 1, а) построен полный граф замкнутой размерной цепи (рис. 3, а). Используя данный граф можно рассчитать любой размер, поскольку он может быть получен суммой или разностью двух других. Например, размер С, соответствующий ребру (1, 3), равен сумме размеров А и В, соответствующих ребрам (1, 2) и (2, 3). Для неидеальных деталей на рис. 3, б–г, представлены возможные размерные цепи. На этих рисунках замыкающее звено изображено пунктирной линией. Авторы отмечают практическую полезность и удобство использования размерных цепей в виде графов, поскольку допуск замыкающего звена легко может быть рассчитан как сумма допусков составляющих граф звеньев. Кроме того, стоит отметить, что различные варианты графов размерных связей описывают разные по функциональному назначению детали, технологии изготовления которых также отличаются.
а) б) в) г)
Рис. 3. Представление структуры расположения плоскостей детали (рис. 1): а) идеальное; б), в), г) реальные варианты размерных цепей
Окончательно модель представления геометрического образа выглядит в виде указанного графа с приписанными для каждой вершины (поверхности) и каждого ребра (размерной связи) совокупности их параметров.
Научная новизна подхода заключается в том, что построение графов размерных связей во всех шести направлениях Xl, Yl, Zl, Xα, Yα и Zα позволяет описать взаимное расположение всех поверхностей детали, а также сформировать схемы порождения геометрической конфигурации детали.
Схема порождения геометрической конфигурации детали
Авторы предлагают новый способ формирования схемы порождения геометрической конфигурации детали на основе графов размерных связей. Например, деталь, изображенная на рис. 1, б, и имеющая граф размерных связей, изображенный на рис. 3, б, может быть изготовлена тремя способами. Первый способ: сначала изготавливается поверхность 1, затем от нее, согласно заданному размеру, формируется поверхность 2, и от поверхности 2 – поверхность 3. Второй способ: изготовление начинается с поверхности 3, затем от нее формируется поверхность 2 и в последнюю очередь от поверхности 2 изготавливается поверхность 3. Третий способ: изготавливается поверхность 2, а от нее изготавливаются поверхности 1 и 3.
Используя совокупности графов размерных связей по всем шести направлениям, можно автоматически сформировать все возможные способы порождения геометрической конфигурации реальной детали с учетом требований к взаимному расположению поверхностей [1, 6]. Предложенный способ обладает как научной новизной, так и практической полезностью. Авторами проведена серия экспериментов по формированию схем порождения геометрической конфигурации для различных деталей, а также анализ и сравнение полученных данных с разработанными технологическими процессами.
Заключение
Как показали исследования в области моделирования геометрической конфигурации объектов в трехмерном пространстве, использование в качестве базиса шестимерного пространства, соответствующего всем степеням свободы, позволяет создать формальную основу для принципиально новых ядер CAD, CAM и CAE систем.
Предложенный авторами подход к описанию геометрической конфигурации реальных объектов позволяет описывать неточности формы и расположения поверхностей, а также структуру их взаимоотношений при конфигурировании объектов. Кроме того, предлагаемая концепция рассматривает и описывает технологии порождения неидеальных объектов.
Данный подход может быть использован для автоматизированной разработки технологических процессов изготовления деталей машин.
Работа выполнена при финансовой поддержке Министерства образования и науки Российской Федерации по Государственному контракту № 02.G25.31.0173
Библиографическая ссылка
Лелюхин В.Е., Игнатьев Ф.Ю., Дренин А.С., Колесникова О.В. ГЕОМЕТРИЯ ДЛЯ ОПИСАНИЯ РЕАЛЬНЫХ ДЕТАЛЕЙ МАШИН // Современные наукоемкие технологии. 2018. № 8. С. 95-99;URL: https://top-technologies.ru/ru/article/view?id=37126 (дата обращения: 28.01.2026).



